Вычислительные системы и сет.тех(магистр) / Лабораторная работа2

Введение

На современном уровне техники сложность объектов зачастую не позволяет разработать для них эффективных математических моделей и тем более -

аналитических методов их решения. К тому же составление мат. модели и проведение расчёта требует определённой квалификации. Таковы две причины всё большего распространения численных методов.

Основой численных методов являются не менее сложные математические теории, их главное отличие - возможность значительно уменьшить долю ручных вычислений и корректировок мат. модели. Такое упрощение компенсируется необходимостью многократного повторения расчётных шагов - «итераций», однако для современных компьютеров это зачастую не является проблемой.

2

Ход работы

Метод Монте-Карло заключается в следующем: для целевой случайной величины генерируется набор случайных значений, а затем на его основе рассчитываются требуемые значения.

Современный вариант метода сформировался в рамках Манхэттенского проекта, где он применялся для моделирования расстояний, которые могут пройти нейтроны в различных материалах. Рассмотрим вычисление числа Пи с помощью метода Монте-Карло.

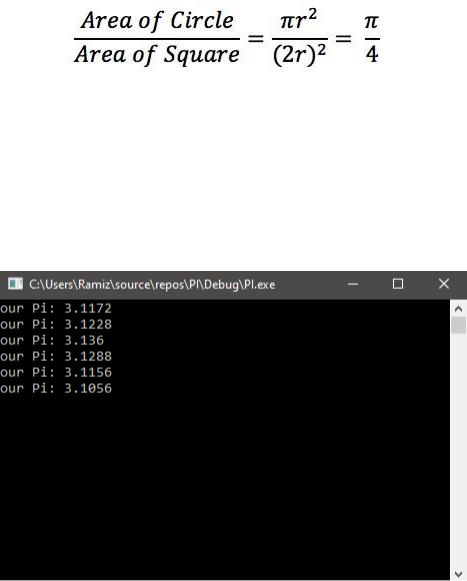
Вписав круг в квадрат, можно выразить отношение площади круга к площади квадрата следующим образом:

Если мы сможем вычислить это отношение, значит, мы сможем получить значение числа Пи.

Заполним квадрат точками со случайными координатами. Рассчитаем отношение количества точек, попавших в круг, к общему количеству точек.

Умножим результат на 4, чтобы получить значение числа Пи. Результат работы программы представлен на рисунке1.

Рисунок 1 –работа программы на c++

3

Код программы:

#include "pch.h" #include <iostream> #include <chrono> #include <thread> #include <functional>

using namespace std;

void timer_start(std::function <void(void)> func,unsigned int interval)

{

std::thread([func, interval]() { while (true)

{

func(); std::this_thread::sleep_for(std::chrono::milliseconds(interval));

}

}).detach();

}

int main() {

::std::srand((unsigned int)::std::time(NULL));

int iterations = 10000; int points = 0;

int a = 0; int b = 0; // int d;

for(int j = 0; j < 6;j++) {

for (int i = 0; i < iterations; i++) { a = (rand() % (100 + 1));

b = (rand() % (100 + 1));

if ((a * a + b * b) < (100 * 100)) points++;

};

a = 0; b = 0;

cout << "our Pi: " <<(float)4 * points / iterations << std::endl; points = 0;

}

while (true); return 0;

}

При выполнении работы было замечено, что при малом количестве итераций точность числа Pi уменьшается. В лабораторной работе мы подобрали оптимальное количество итераций, а именно 10000. Далее мы в Excel вычислим число ПИ с помощью метода Монте-Карло. Результат работы представлен на рисунке 2.

4

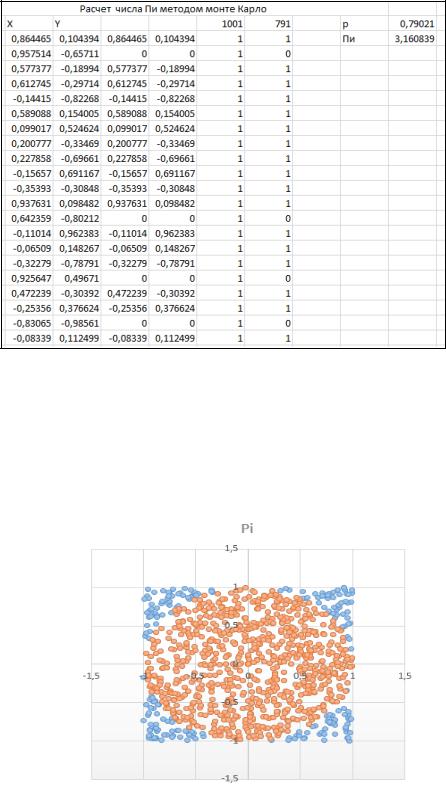
Рисунок 2 – метод Монте-Карло в Excel

Для подсчета и построения числа Пи с помощью нашего метода нам нужны две точки координат X и Y. С помощью СЛУЧ() мы сделали выборку для каждой точки, доесть 1000 случайно генерированных значений. Подсчитали кол-во точек на окружности и за ее приделами. График разброса точек координат представлен на рисунке 3.

Рисунок 3 – график разброса точек координат

Далее мы подсчитали p(вероятность). Для этого мы подсчитали точки не лежащими на окружности с общим количеством и поделили их. После получения вероятности мы умножили ее на 4 и получили число Пи. В Excel точность зависит от количества точек, чем больше, тем точней.

5

Заключение

В ходе работы мы рассмотрели и вычислили числа Пи с помощью метода Монте-Карло. Обнаружили, что точность зависит от количества итераций и точек, чем больше их, тем лучше результат. Убедились, что соотношение общего кол-ва точек и кол-ва точек, попавших в круг примерно равно соотношению площади квадрата и площади круга. Для нашего метода использовали метод rand и параметр если() отличающиеся друг от друга генерацией случайных чисел, что тоже имеет роль в конечном результате.

6