
Вычислительные системы и сет.тех(магистр) / Лабораторная работа1
.pdf
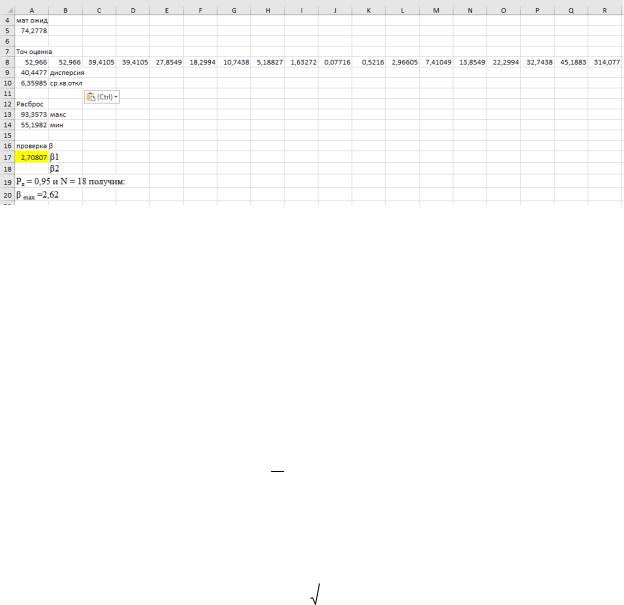
Проверка расчетов статической обработки результатов эксперимента.
Рисунок 1 – измерения с помощью Excel
Для полученной выборки из 18 (N = 18) измерений провести статистическую обработку результатов эксперимента.
Данные в выборке:
67 |
67 |
68 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
92 |
Последовательность выполнения задания:
Проанализируем ряд в целях обнаружения грубых ошибок и промахов. Точечная оценка математического ожидания вычисляется по формуле (1):
|
|
1 |
xi |
(1) |
|
X = |
|||||
N |
|||||
|
|
|
|
||
= 74.28
С помощью формул (2, 3) вычислим точечную оценку среднеквадратичного отклонения:
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Sx2 = |
|
|
( xi − X )2 |
(2) |
||||||||
N − |
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
Sx |
= |
Sx2 |
(3) |
||||||||
|
|
|
|
Sх = 6,36. |
|
|||||||
Пользуясь правилом трех сигм, по формуле (4), вычисляем допустимый |
||||||||||||
разброс случайных величин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||
xmax/ min = X 3 = X 3Sx |
||||||||||||
Xmax, min = 74,28 ± |
3·6,36 = 93,36...55,2. |
|||||||||||
По данному критерию грубой ошибки в ряде нет. Однако значение 92 следует |
||||||||||||
проверить с помощью критерия β. По формулам (5), |
(коэффициент β1 используют |
|||||||||||
для максимального значения в выборке): |
|
|
|
|
|
|
||||||
2
|
|
|
|
|
|
|
|
|
1 |
= |
xmax |
− X |
|
; |
(5) |
||
|
|
|
|
|
||||
|
||||||||
|
|
|
N −1 |
|
||||
Sx 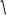 N
N
1 = 92 − 74.22 = 2.71. 6.2 √17/18
При доверительной вероятности Pд = 0,95 и N = 18 получим: β max =2,62.
Так как 2,71 < βmax, измерение 92 не является грубым промахом. В технических расчетах обычно принимают доверительную вероятность Pg = 0,95, поэтому проверим соответствующее такой вероятности значение βmax.
Если РД = 0,95, N=18, получим из таблицы 3 βmax=2,62 в этом случае 2,71 > и значение 92 следует исключить как грубый промах. Запишем очищенный
ряд (N=17):
67 |
67 |
68 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
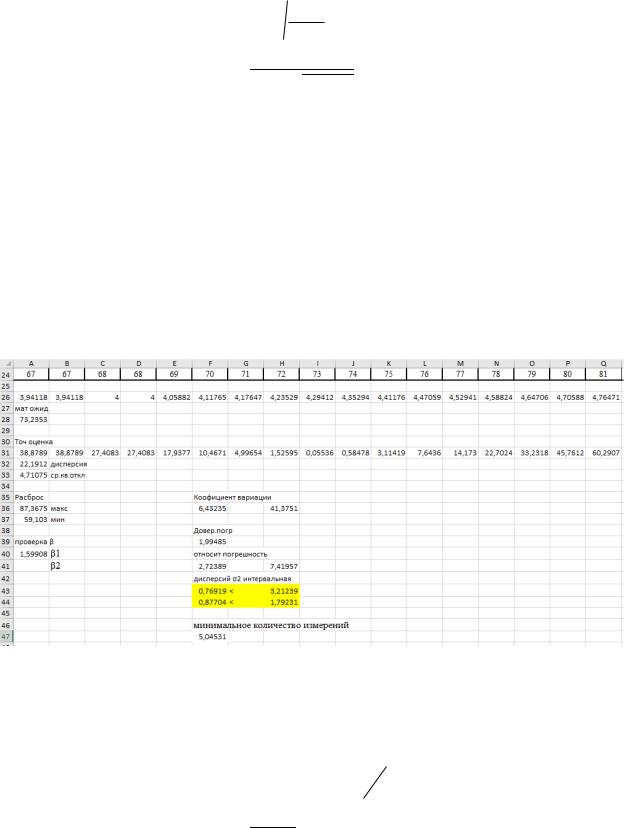
Рисунок 2 – измерения с помощью Excel
По формулам (1-3) найдем точечные оценки очищенного ряда:
|
|
2 |
|
|
= 73.24; |
= 22.19; |
= 4.71. |
||
|
|
|
|
|
По формуле (6) вычисляем коэффициент вариации:
КВ = 100% Sx |
|
(6) |
|
X |
|||
|
|
4.71= 73.24 100% = 6.43.
3

Найдем интервальные оценки очищенного ряда. Поскольку N < 30, ряд следует отнести к малой выборке, и доверительный интервал вычисляется с применением коэффициента Стьюдента t.
При PД= 0,95 и f=17-1=16 коэффициент Стьюдента t = 1,746. Доверительный интервал вычисляем по формуле (7) при N = 17:
= |
Sx t |
(7) |
||
|
|
|
||
|
N |
|||
|
|
|
||
= ± 4.71 1.746 = 1.99. √17
Относительную погрешность результатов измерений вычислим по формуле 8:
= 100% |
|
(8) |
|
X |
|||
|
|
1.99= 73.24 100% = 2.72%.
Истинное значение измеряемой величины:
Д = ± = 73.24 ± 1.99
Найдем интервальную оценку дисперсии σ2 по формуле (9) при уровне значимости α = 1 - 0,95 = 0,05:
|
|
|
|
f Sx2 |
2 |
|
|
|
|
f Sx2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9) |
|
|
|
x |
2 |
|
|
|
|
x |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 f ; 1−0.5 |
|
|
|
|
1 f ; 0.5 |
|
||||||
|
|
0,77 ≤ σ2 ≤ 3,21 |
|
|
|
|
|||||||||
Найдем интервальную оценку среднеквадратичного отклонения по формуле |
|||||||||||||||
(10): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
fSx2 |
|
|
fSx2 |
|
|
|
(10) |
|||||
|
|
|
x2 |
|
x2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
0,88 ≤ σ < 1,79 |
|
|
|
|
||||||||
Пусть необходимая точность измерений составляет 5%. Определим минимальное количество измерений для достижения заданной точности. По формуле (17):
|
|
|
К 2 |
t2 |
|
||
|
Nmin = |
В |
|
|
|
(17) |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
||
|
|
6.432 1.7462 |
|
= 5,04 |
|||
52 |
|
|
|||||
|
|
|
|||||
Для достижения заданной точности достаточно сделать 6 измерений.
1. Аппроксимация функций
x |
0,034 |
0,394 |
0,754 |
1,114 |
1,474 |
1,833 |
2,193 |
2,553 |
2,913 |
(время, ч) |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
y |
5,156 |
5,983 |
6,577 |
6,708 |
6,802 |
6,9 |
7,067 |
7,129 |
7,171 |
|||
(твёрдость, |
|
|
|
|
|
|
|
|
|
|
|
|
HB) |
|
|
|
|
|
|
|
|
|
|
|
|
Методом аппроксимации построил график зависимости твёрдости |
||||||||||||
детали от времени выдержки. Сравнил при этом точность различных |
||||||||||||
функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полиминиальная |
|
|
|
|
|
|||
8 |
|
|
|
|
|
|
|
y = 5,5607e0,0336x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,034 |
0,394 |
0,754 |
1,114 |
1,474 |
1,833 |
2,193 |
2,553 |
2,913 |
|
||
|
|
Рисунок 3 – Полиномиальная диаграмма |
|
|
|
|||||||
|
|
Степенная |
|
|
|
|
||
8 |
|
|
|
|
|
y = 5,5607e0,0336x |
|
|
7 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0,034 |
0,394 |
0,754 |
1,114 |
1,474 |
1,833 |
2,193 |
2,553 |
2,913 |
|
Рисунок 4 – Степенная диаграмма |
|
|
|||||
5
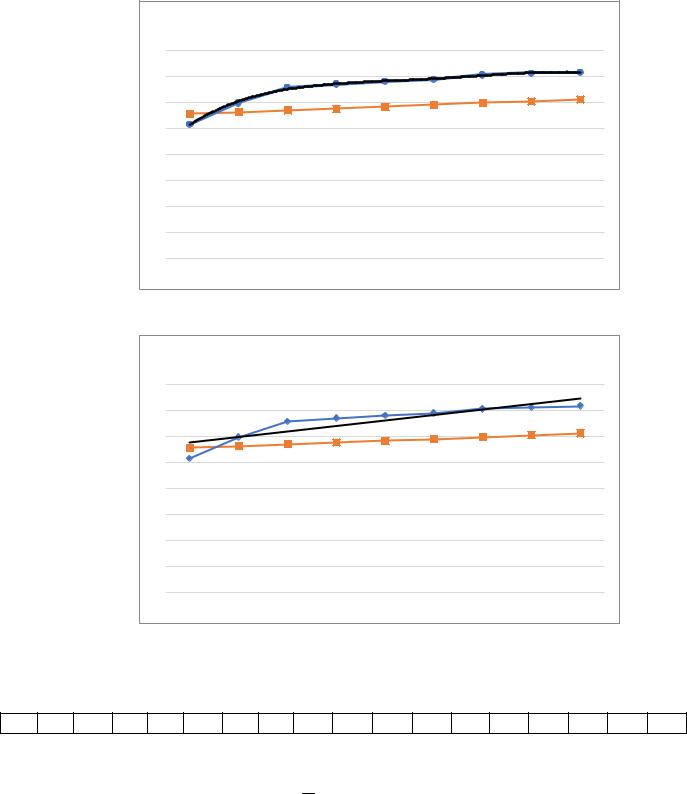
|
|
Логарифмическая |
|
|
|
|||
8 |
|
|
|
|
|
y = 5,5607e0,0336x |
||
7 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0,034 |
0,394 |
0,754 |
1,114 |
1,474 |
1,833 |
2,193 |
2,553 |
2,913 |
|
Рисунок 5 – Логарифмическая диаграмма |
|
||||||
|
|
Линейная |
|
|
|
|
|
|
8 |
|
|
|
|
|
y = 5,5607e0,0336x |
||
7 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0,034 |
0,394 |
0,754 |
1,114 |
1,474 |
1,833 |
2,193 |
2,553 |
2,913 |
|
Рисунок 6 – Линейная диаграмма |
|
|
|||||
Для оценки точности замеров твёрдости, в одной из точек было проведено 18 измерений твёрдости заготовки:
6,31 6,32 6,15 6,23 6,25 6,42 6,25 6,30 6,84 6,31 6,35 6,37 6,41 6,42 6,14 6,46 6,23 6,52
Точечная оценка математического ожидания вычисляется по формуле (1):
= 74.28
С помощью формул (2, 3) вычислим точечную оценку среднеквадратичного отклонения:
Sх = 6,36.
6
Заключение
Было проведено повторный расчет статистической обработки результатов эксперимента по выборке из 18. Найдены отличия в расчетах. Взято другое значение доверительной вероятности, но данное значение не особо критическое. Найдены интервальные оценки дисперсии и оценка среднеквадратичного отклонения, эти оценки в результате дали иное значение.
Витоги задания достижение заданной точности решение верно.
Взадании аппроксимация функций были рассчитаны характеристики точности измерений и построены графики зависимости твердости детали от времени выдержки. Линия тренда ближе всего по значения к логарифмической аппроксимации.
7
