
Никитина Дарья ПИН-21Д КР2
.docx
Контрольная
работа №2
Математическая
логика и теория алгоритмов
Никитина
дарья пин-21Д



Задание 1.
Построим
биекцию между множеством всех таких
рядов и декартовым произведением Q
(множества рац. чисел) на себя счётное
число раз, сопоставив ряд
 последовательности
последовательности
 .
Ясно, что |QN| = |NN|,
т.к. Q счётно (где N множество нат.
чисел, AB — множество
функций из B в A). Теперь имеем
неравенства |NN|
.
Ясно, что |QN| = |NN|,
т.к. Q счётно (где N множество нат.
чисел, AB — множество
функций из B в A). Теперь имеем
неравенства |NN|
 |(2N)N| = |2(N
x N)|
= |2N| = C и
|NN|
|(2N)N| = |2(N
x N)|
= |2N| = C и
|NN|
 |2N| = C, так
что по теореме Кантора - Бернштейна
ответ - континуум.
|2N| = C, так
что по теореме Кантора - Бернштейна
ответ - континуум.
Задание 2.
Построим
биекцию, сохраняющую порядок, из левой
части в правую. Элементы (n, x)
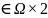 отправим в (n, x)
отправим в (n, x)
 (где
(где
 — значок принадлежности), а элементы
из второго слагаемого
— значок принадлежности), а элементы
из второго слагаемого
 отправим в (n, 2)
.
То, что это биекция, очевидно. Она
сохраняет порядок на элементах каждого
слагаемого по отдельности, и все элементы
первого слагаемого переходят в элементы,
меньшие всех образов элементов второго
слагаемого, так что биекция сохраняет
порядок.
отправим в (n, 2)
.
То, что это биекция, очевидно. Она
сохраняет порядок на элементах каждого
слагаемого по отдельности, и все элементы
первого слагаемого переходят в элементы,
меньшие всех образов элементов второго
слагаемого, так что биекция сохраняет
порядок.
Задание 3.
Используем лемму Цорна. Пусть X наше упорядоченное множество, C цепь. Возьмём множество всех цепей в X, содержащих C, обозначим это множество через M. В нём порядок получается из отношения включения цепей. Нам нужен максимальный элемент в M, по условию. Лемма Цорна говорит, что такой элемент существует, если любая непустая цепь в M имеет верхнюю грань (тут ещё важно, что M непусто, оно содержит C).
Итак, пусть
L непустая цепь в M, это семейство
цепей в X, любые два из которых связаны
отношением включения. Возьмём объединение
всех элементов L, обозначим его D.
Это подмножество X, содержащее все
элементы L, так что остаётся проверить,
что D цепь. Пусть a, b
D.
По определению, найдутся A, B
L такие, что a
A, b
B. Т.к. L цепь, то, не умаляя общности,
A подмножество B. Следовательно,
a, b
B.
Так как B цепь, то a
 b или b
a.
И так для всех a, b
D,
то есть D — это цепь.
b или b
a.
И так для всех a, b
D,
то есть D — это цепь.
