Никитина ДС Лабораторная работа 1

Лабораторная работа №1

Компьютерный практикум по линейной алгебре и аналитической геометрии

Никитина Дарья Пин-21д

Упражнение 1.1

Наберите в командной строке 1+2 и нажмите <Enter>.

Код:

>> 1+2

ans =

3

Если требуется продолжить работу с предыдущим выражением, например, вычислить (1+2)/4.5, то проще всего воспользоваться уже имеющимся результатом, который хранится в переменной ans. Наберите в командной строке ans/4.5 (при вводе десятичных дробей используется точка) и нажмите <Enter>

Код:

>> ans/4.5

ans =

0.6667

>>

Упражнение 1.2

1) сложите два числа 1/2+2/3 в формате format short

2) перейдите в формат format rational и сложите два числа 1/2+2/3

Код:

>> format short

>> 1/2+2/3

ans =

1.1667

>> format rational

>> 1/2+2/3

ans =

7/6

>>

Упражнение 1.3.

Введите

>> (x+1)*(x-1)

Код:

>> (x+1)*(x-1)

Undefined function or variable 'x'.

теперь введите

>> syms x

>> f=(x+1)*(x-1)

>> collect(f)

Код:

>> syms x

>> f=(x+1)*(x-1)

f =

(x - 1)*(x + 1)

>> collect(f)

ans =

x^2 - 1

>>

Ответьте в отчете на вопрос, что сделала команда collect с выражением f

Преобразовала функцию в вид суммы степеней переменной х.

теперь присвоим x какое-нибудь число:

>>x =

2

снова вызовем

>> f

теперь снова вызовем

>> f=(x+1)*(x-1)

Код:

>> x=2

x =

2

>> f

f =

(x - 1)*(x + 1)

>> f=(x+1)*(x-1)

f =

3

>>

Опишите в отчете , что произошло.

Программа запомнила значение переменной х и подставила его вместо символа в формуле, а затем выполнила соответствующие вычисления.

Упражнение

1) Убрать из рабочего пространства все переменные.

2) Ввести новые переменные x, y, z, t, задав им значения соответственно 1, 2, 3, 4.

3) Вывести в командное окно информацию обо всех переменных.

4) Удалить из рабочего пространства переменную x.

5) Вывести в командное окно информацию об оставшихся переменных.

6) Удалить из рабочего пространства одновременно переменные у и z.

7) Вывести в командное окно информацию об оставшихся переменных.

Код:

>> whos

Name Size Bytes Class Attributes

a 1x1 8 double

ans 1x1 112 sym

b 1x1 8 double

c 1x1 8 double

f 1x1 8 double

h 1x1 8 double

x 1x1 8 double

>> clear

>> x=1; y=2; z=3; t=4;

>> whos

Name Size Bytes Class Attributes

t 1x1 8 double

x 1x1 8 double

y 1x1 8 double

z 1x1 8 double

>> clear x

>> whos

Name Size Bytes Class Attributes

t 1x1 8 double

y 1x1 8 double

z 1x1 8 double

>> clear y z

>> whos

Name Size Bytes Class Attributes

t 1x1 8 double

>>

Упражнение 1.4

1. Для задания вектора-строки (т.е. матрицы размера 1m ) используются квадратные

скобки, в которых числовые данные отделяются друг от друга пробелами или запятыми

Код:

>> B=[1 3 -1]

B =

1 3 -1

>> B=[1,3,-1]

B =

1 3 -1

>>

2. Для задания вектора-столбца (т.е. матрицы размера n1 ) используются квадратные

скобки, в которых числовые данные отделяются друг от друга точкой с запятой

Код:

>> C=[-1;2.1]

C =

-1

21/10

>>

3. Комбинируя оба варианта разделителя, можно задать матрицу, число строк и столбцов которой больше одного (двумерный массив):

Код:

>> A=[1 2 3 4; 0 -1 -3 -2]

A =

1 2 3 4

0 -1 -3 -2

>>

4. Любое число рассматривается в MATLAB как матрица размера . 11

Код:

>> n=3

n =

3

>> m=[3]

m =

3

>> whos A B C n m

Name Size Bytes Class Attributes

A 2x4 64 double

B 1x3 24 double

C 2x1 16 double

m 1x1 8 double

n 1x1 8 double

Упражнение 1.5.

Для доступа к отдельным элементам матриц указываются их индексы.

1. Например, A(1,3) – элемент матрицы А, стоящий в 1-й строке и 3-м столбце;

Код:

>> A(1,3)

ans =

3

2. Этот элемент матрицы А можно вызвать иначе

Код:

>> A(5)

ans =

3

3. В(2) и В(1,2) – второй элемент вектора-строки В.

Вызовите эти элементы.

Код:

>> B(2)

ans =

3

>> B(1,2)

ans =

3

Упражнение 1.6

1) Задать вектор-строку a вектора а={1,2,3,4,5}

a) с помощью символов c пробелами;

b) с помощью символов с запятыми;

c) стандартной функцией

d) с помощью двоеточия с шагом можно задать те же числа от 1 до 6 с шагом 1

Код:

>> a=[1 2 3 4 5]

a =

1 2 3 4 5

>> a=[1,2,3,4,5]

a =

1 2 3 4 5

>> a=horzcat(1,2,3,4,5,6)

a =

1 2 3 4 5 6

>> a=[1:1:6]

a =

1 2 3 4 5 6

2)Задать вектор-столбец b ={ 1, 1.9, 2.8, 3.7}

a) с помощью точки запятой «;» ;

b) транспонировав вектор-строку a, с помощью символа «'»-одинарная кавычка (буква э в латинском регистре)

>> a1=a'

с) проделайте то же действие с вектором b

>> b2=b'

d) задайте вектор b стандартной функцией

>> b=vertcat(1, 1.9, 2.8, 3.7)

e) с помощью двоеточия с шагом

>> b4=[1:0.9:4] '

Код:

>> b=[1;1.9;2.8;3.7]

b =

1

19/10

14/5

37/10

>> a1=a'

a1 =

1

2

3

4

5

6

>> b2=b'

b2 =

1 19/10 14/5 37/10

>> b=vertcat(1, 1.9, 2.8, 3.7)

b =

1

19/10

14/5

37/10

>> b=[1:0.9:4]

b =

1 19/10 14/5 37/10

Упражнение 1.7. Функция line

Построить последовательно три прямые

(0,0)______(2,1) , (0,0)______(-2,-1), (-2,4)______(0,0) .

Код:

>> line([0;2],[0;1])

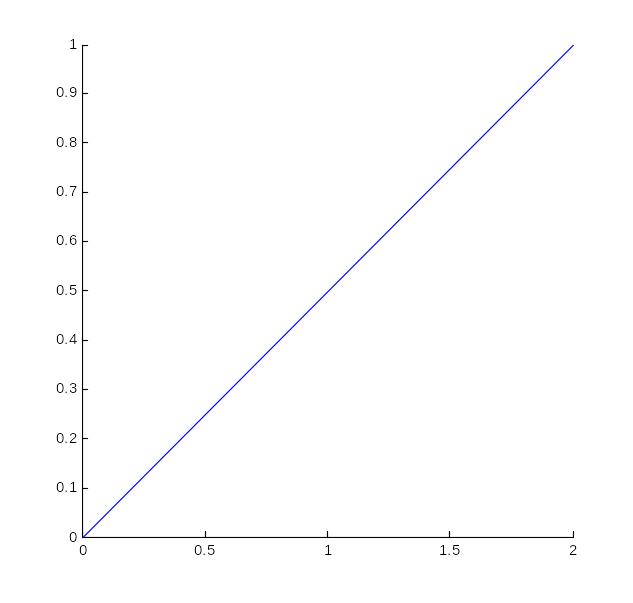
>> line([0;-2],[0;-1])

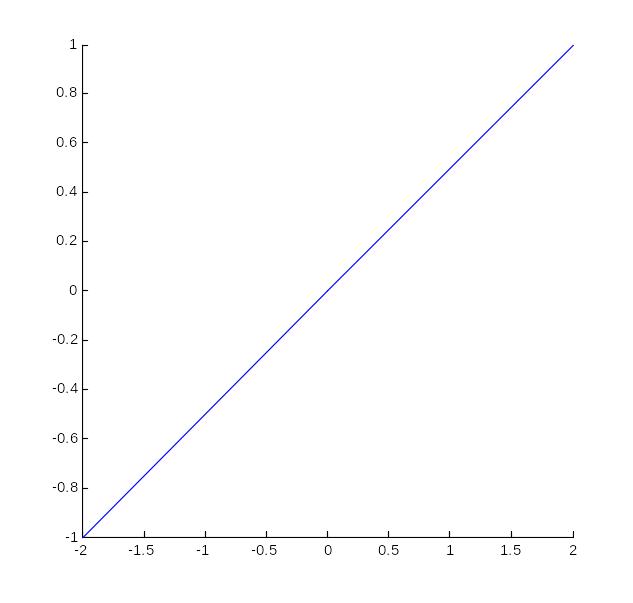
>> grid on

>> line([-2;0],[4;0])

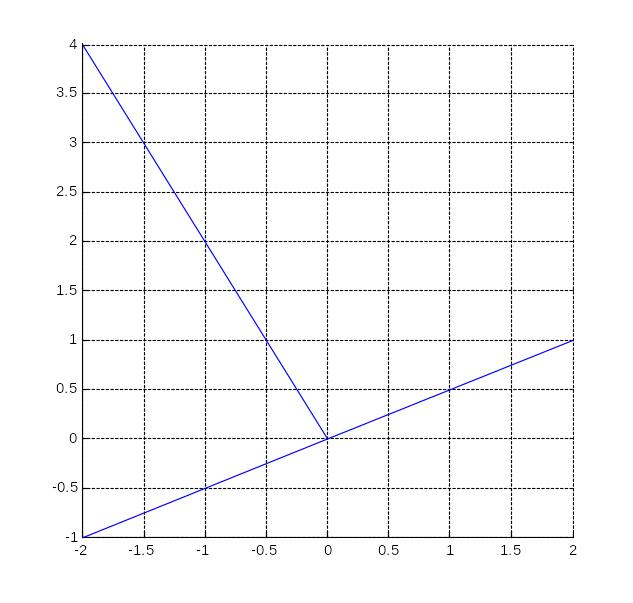
Упражнение 1.8.

Закройте окно Figures.

Построить последовательно

прямые (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .

Код:

>> line([0;2],[0;1])

>> grid on

>> line([0;2],[2;0])

>> line([0;3],[2;0])

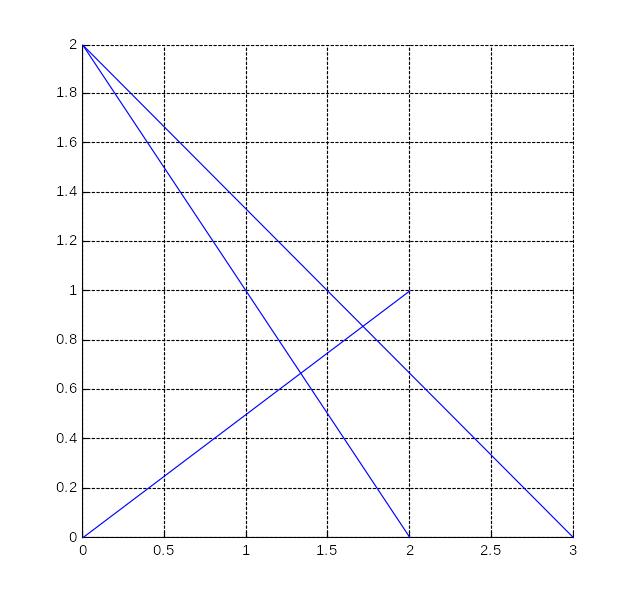
Упражнение 1.9.

Закройте окно Figures.

И теперь построим сразу все три прямые из Упражнения 1.7. с помощью одной функции line.

Код:

>> line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])

>> grid on

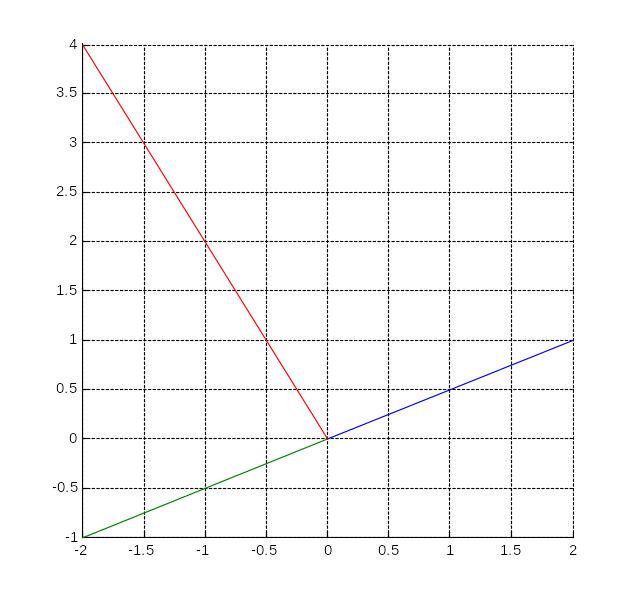
Упражнение 1.10.

Закройте окно Figures.

Постройте три прямые из Упражнения1.8.

(0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) с помощью одной функции line.

Код:

>> grid on

>> line([0,0,0;2,2,3],[0,2,2;1,0,0])

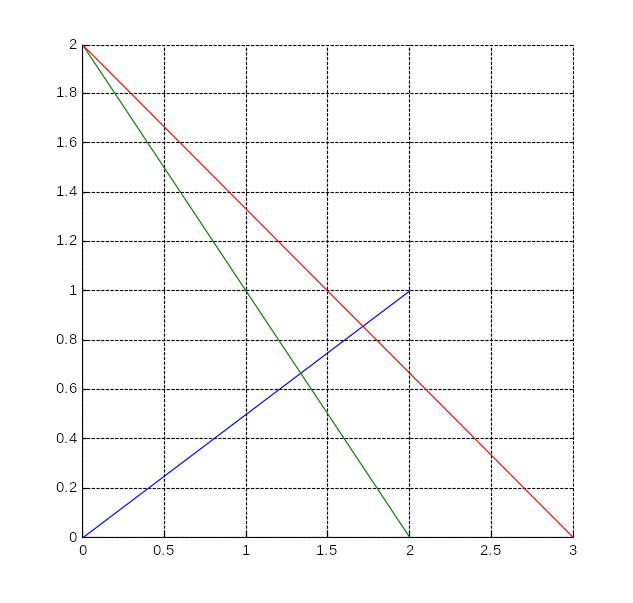
Упражение 1.11.

Создать графическое окно для четырех координатных плоскостей. В первых трех построить по одной прямой, в четвертой все три прямые.

Прямые (0,0)______(2,1) , (0,0)______(-2,-1), (-2,4)______(0,0)

Код:

>> subplot (2,2,1)

>> grid on

>> line([0;2],[0;1])

>> subplot (2,2,2)

>> grid on

>> line([0;-2],[0;-1])

>> subplot (2,2,3)

>> grid on

>> line([-2;0],[4;0])

>> subplot (2,2,4)

>> grid on

>> line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])

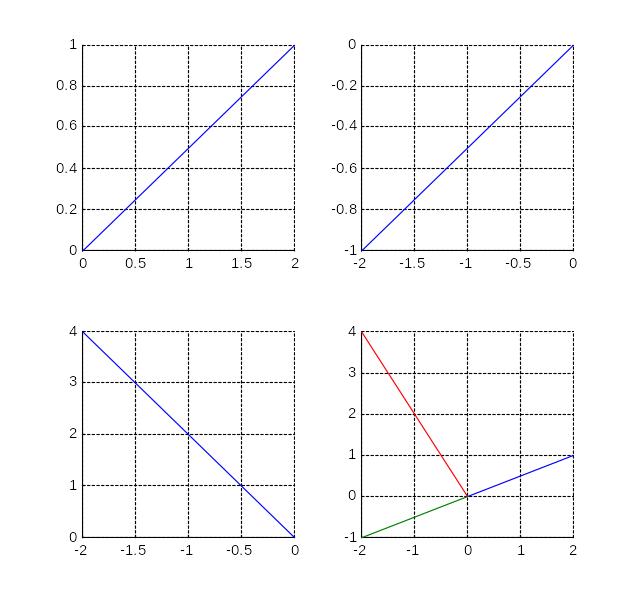
Упражение 1.12.

Создать графическое окно для четырех координатных плоскостей. В третьей области построить все три прямые, в остальных по одной.

Прямые:

(0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .

Код:

>> subplot(2,2,1)

>> grid on

>> line([0;2],[0;1])

>> subplot(2,2,2)

>> grid on

>> line([0;2],[2;0])

>> subplot(2,2,4)

>> grid on

>> line([0;3],[2;0])

>> subplot(2,2,3)

>> grid on

>> line([0,0,0;2,2,3],[0,2,2;1,0,0])

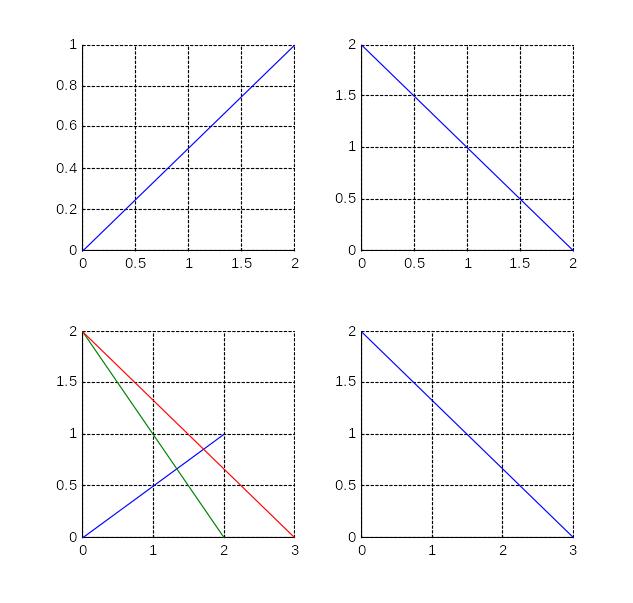
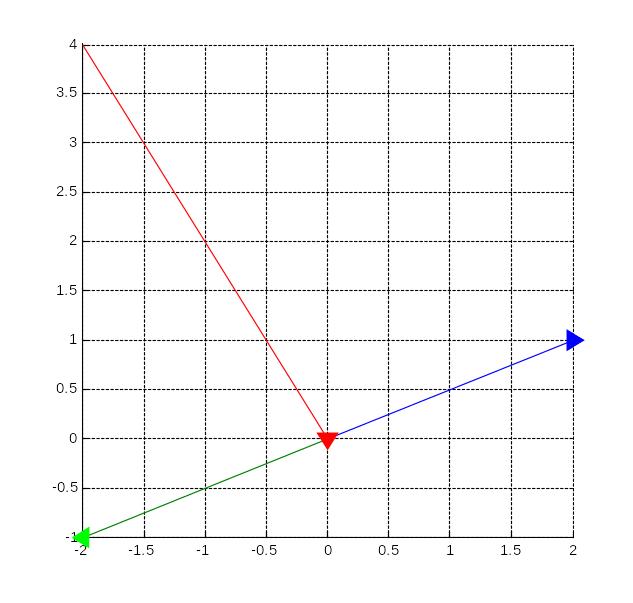
Упражнение 1.13

Построить векторы, взяв за их основу прямые:

(0,0)______(2,1) , (0,0)______(-2,-1), (-2,4)______(0,0), отметив концы в соответствующих точках.

Код:

>> line([0,0,-2;2,-2,0],[0,0,4;1,-1,0])

>> grid on,hold on

>> plot(2,1,'>b','lineWidth',4)

>> plot(-2,-1,'<g','lineWidth',4)

>> plot(0,0,'vr','lineWidth',4)

Упражнение 1.14.

Построить векторы для прямых (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .

Код:

>> line([0,0,0;2,2,3],[0,2,2;1,0,0])

>> grid on,hold on

>> plot(2,1,'>b','lineWidth',4)

>> plot(2,0,'vg','lineWidth',4)

>> plot(3,0,'>r','lineWidth',4)