
3
.pdf
---------------------------------------------------------------Упр. 3.16.(конец)
Таким образом, для решения и исследования других подобных задач, можно договориться, что первый вектор правой тройки мы рисуем синим цветом, второй - зеленым, а третий - красным цветом.
Упражнение 3.18.
Вычислить площадь треугольника с вершинами A (1; 3; 1), B (2; 1; 4) и C (5; 0; 3).
Изобразить плоскость треугольника. Как соотносятся площадь треугольника и векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением.
Смешанное произведение |
|
|
|
|
Смешанным произведением векторов a,b, c (обозначается: |
a,b, c или a b c ) |
|||
называется число |
a,b,c a, b c. |
(10) |
|
|
|
|
|
|
|
Свойства смешанного произведения: |
|
|
||
a,b,c b,c, a |
c, a,b ; |
|
(11) |
|
b, a,c c,b, a |
a,c,b a,b,c ; |
(12) |
|
|
|
|
; a,b,c a,b,c . |
(13) |
|
a a , b, c a, b, c a , b, c |
||||
Свойства (11) и (12) означают, что смешанное произведение не изменяется при круговых перестановках аргументов и умножается на 1 при других перестановках. Свойства (13) выражают линейность смешанного произведения векторов по первому аргументу. Имеет место также линейность по второму и третьему аргументу.
Геометрический смысл смешанного произведения
Пусть V Va,b,c – объём параллелепипеда, построенного на векторах a,b, c
(считается, что Va,b,c 0, если a, b, c компланарны). Тогда
21
|
|
V , если a, b, c правая тройка, |
|
a,b,c |
(14) |
V , если a, b, c левая тройка. |
|
|
|
Выражение смешанного произведения через координаты векторов |
|
Пусть e1, e2 , e3 |
– базисные векторы некоторой системы координат Oxyz (вообще |
говоря, косоугольной). Если a a1e1 a2e2 a3e3 , b b1e1 b2e2 b3e3 , c c1e1 c2e2 c3e3 ,
то
a1 a2 a3
a,b,c b1 b2 |
b3 e1,e2 ,e3 . |
(15) |
c1 c2 c3
Если же система координат прямоугольная и базисные векторы i e1, j e2 , k e3
образуют правую тройку, то
|
a1 |
a2 |
a3 |
|
|
a,b, c |
b1 |
b2 |
b3 |
. |
(16) |
|
c1 |
c2 |
c3 |
|
|
Замечание. Формула (15) верна и в случае, если векторы e1, e2 , e3 не образуют базиса (но векторы a,b, c выражены через них) – в этом случае левая и правая части равенства (15) равны 0.
Условие компланарности векторов |
|
a,b, c компланарны a, b, c 0. |
(17) |
Упражнение 3.19.
Найти смешанное произведение векторов a,b, c , где векторы и перемножаются векторно, а их результат на вектор скалярно, см формулу (10). Затем найти смешанное произведение по формуле
(16).
Проверить свойства (11) и (12) смешанного произведения по формуле (10).
Упражнение 3.20.
С помощью смешанного произведения доказать, что векторы , и компланарны, определить ориентацию этой тройки. Ответьте на вопрос: как это связано понятие компланарность с понятиями базис и линейная зависимость для этих векторов. Построить эти векторы. Вектор изобразить синим, вектор зеленым, вектор красным.
22

Упражнение 3.21.
Исследовать с помощью смешанного произведения векторы  на компланарность , векторы a,b, c -некомпланарны, их смешанное произведение равно +1.
на компланарность , векторы a,b, c -некомпланарны, их смешанное произведение равно +1.
A) 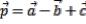 ,
, 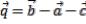 и
и 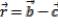 ,
,
B) 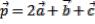 ,
, 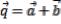 и
и 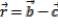 ,
,
C) 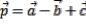 ,
, 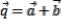 и
и 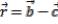 .
.
Упражнение 3.22.
Вычислить  a 2b c, 3a b, 2a 2b c
a 2b c, 3a b, 2a 2b c  , если
, если  a,b, c
a,b, c  =А.
=А.
Упражнение 3.23.
Пусть a, b, c – некомпланарные векторы. Найти значение , при котором следующие
векторы компланарны: p a 2b c, q 3a b c, r a c.
Задачи для самостоятельного решения
1. Даны векторы a (1; 2; 3), b (1; 0; 3), c (0; 4; 1).
Вычислить: а)[a 2b, a c]; б) a,b ,c a, b,c ; в) [a,b], [a,c] .
2.Вычислить  a, b, c
a, b, c  , если
, если  2a b, a 3b c, b c
2a b, a 3b c, b c  5. Ответ: 95 .
5. Ответ: 95 .
3.При каких векторы a (3; 1; 4), b (1; 0; 3), c ( ; 2; 1), взятые в указанном порядке, образуют правую тройку?
4.Вычислить 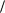 2i 3 j 5k , i j, 2 j k
2i 3 j 5k , i j, 2 j k 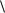 .
.
5.Для определения длины вектор-столбцов или вектор-строк служит
встроенная функция length:
>> length(s1) ans =
4
Придумать программу для вычисления длины вектора.
Отметим, что векторное и смешанное произведение векторов (наряду со скалярным произведением) используется не только для вычисления площадей и объёмов, но является одним из основных инструментов для исследования прямых и плоскостей в
23
пространстве (задач на составление уравнений прямых и плоскостей, взаимное расположение прямых и плоскостей и т.д.).
24
