Добавил:

euroduck97 ac3402546@gmail.com Направление обучения: транспортировка нефти, газа и нефтепродуктов группа ВН (Вечерняя форма обучения) Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный университет нефти и газа им. И.М. Губкина

Предмет:

Автоматизация производственных процессов

Файл:

2015 [Тынчеров] Основы автоматизации ТПНП

.pdf

Скачиваний:

275

Добавлен:

06.06.2021

Размер:

7.18 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 373 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

xmin

x xmin

q qном

,	(1.6)
,	(1.7)

где φ — относительное значение регулируемой величины; x — сама регулируемая величина;

— минимальное значение регулируемой величины (при но-

минальном режиме);

xmin и qном — базовые значения величин;

λ — относительное значение нагрузки.

Тогда неравномерность δ (или статизм) системы в общем случае есть частная производная в данной точке (или относительная крутизна характеристики регулирования в этой точке):

	.	(1.8)

Если характеристика регулирования линейная, то статизм будет постоянной величиной для всех значений нагрузки. И он может быть определен следующим образом:

xmax xmin

max

xmin

xmax xmin

(1.9)

qном 0

max

xmin

qном

Статический регулятор поддерживает не строго постоянное значение регулируемой величины, а с ошибкой, которая называется статической ошибкой системы. Таким образом, статизм регулирования

— это относительная статическая ошибка при изменении нагрузки от холостого хода до номинальной нагрузки.

Внекоторых системах статическая ошибка (даже если и сотые доли процента) нежелательна, тогда переходят к регулированию, при котором она равна нулю, — к астатическому регулированию. Характеристика регулирования такой системы представляется линией, параллельной оси нагрузки.

Астатическим называется автоматическое регулирование, при котором при различных постоянных значениях внешнего воздействия на объект отклонение регулируемой величины от заданного значения по окончании переходного процесса становится равным нулю.

Вастатическом регуляторе уровня Н воды в баке (рис. 1.7) поплавок перемещает ползунок реостата в ту или иную сторону в зави-

симости от изменения уровня от заданного значения, тем самым запитывая двигатель, управляющий положением заслонки. Выключен двигатель будет тогда, когда уровень воды достигнет заданного значения.

Система астатического регулирования имеет следующие характерные особенности:

—равновесие системы имеет место только при одном значении регулируемой величины, равном заданному;

—регулирующий орган имеет возможность занимать различные положения при одном и том же значении регулируемой величины.

В реальных регуляторах первое условия выполняется с некоторой погрешностью. Для выполнения второго условия в контур регулирования вводится так называемое астатическое звено. В приведенном примере — двигатель, обладающий тем свойством, что при отсутствии напряжения его вал неподвижен в любом положении, а при наличии напряжения он непрерывно вращается.

	а)	б)
	3
	Ø +	4
		4
+ Ø	• • • •
- Ø	• • • •	H
- Ø
1	Ø -
q1		2
		2

q	0	q
		q

Рис. 1.7 — Астатический регулятор уровня воды непрямого действия: а — схема регулятора, б — характеристика регулятора; 1 — задвижка, 2 — поплавок, 3 — электродвигатель постоянного тока, 4 — реостат

Взависимости от источника энергии, получаемой регулятором, различают:

прямое,

непрямое регулирование.

Всистемах прямого регулирования энергия для перестановки управляющего элемента получается от датчика (как пример — статический регулятор уровня воды).

Всистемах непрямого регулирования энергия для перестановки управляющего элемента получается от постороннего источника (пример — астатический регулятор уровня воды).

Системы автоматического регулирования с несколькими регулируемыми величинами (например, давление пара в котле, подача воды

вкотел, подача топлива и воздуха в топку) подразделяются на системы несвязанного и связанного регулирования.

Системами несвязанного регулирования называются такие, в

которых регуляторы, предназначенные для регулирования различных величин, не связаны друг с другом и могут взаимодействовать только через общий для них объект регулирования. Если в системе несвязанного регулирования изменение одной из регулируемых величин влечет за собой изменение других регулируемых величин, то такая система называется зависимой; а если не влечет, то система назы-

вается независимой.

Системами связанного регулирования называются такие, в ко-

торых регуляторы различных регулируемых величин связаны друг с другом и помимо объекта регулирования.

Система связанного регулирования называется автономной, если связи между входящими в ее состав регуляторами таковы, что изменение одной из регулируемых величин в процессе регулирования не вызывает изменения остальных регулируемых величин.

Замкнутые системы автономного регулирования, имеющие только одну (главную) обратную связь, называются одноконтурными. Системы автоматического регулирования, имеющие помимо одной главной обратной связи еще одну или несколько главных или местных обратных связей, называются многоконтурными.

Взависимости от вида характеристик элементов, из которых состоят системы, все системы делятся на:

линейные,

нелинейные.

Линейными называются системы, которые состоят только из элементов, имеющих линейные характеристики; переходные процессы в таких элементах описываются линейными дифференциальными уравнениями.

Нелинейными называются системы, которые имеют один или несколько элементов с нелинейными характеристиками; переходные процессы в таких системах описываются нелинейными дифференциальными уравнениями.

При классификации по виду используемой энергии все системы можно подразделить на:

электрические,

гидравлические,

пневматические,

электрогидравлические,

электропневматические и др.

Взависимости от числа регулируемых величин системы автома-

тического регулирования (САР) бывают:

одномерные,

двухмерные,

многомерные.

Многомерные САР могут быть системами несвязанного и связанного регулирования. Система связанного регулирования может быть автономной [42, 43].

1.1.3. Алгоритм (закон) регулирования

Всякую систему автоматического регулирования можно рассматривать как вычислительное устройство, которое вырабатывает регулирующее воздействие в функции от величины рассогласования ε, нагрузки q и других величин.

А сама функциональная связь (функциональная зависимость) между желаемым регулирующим воздействием на объект yо, величиной рассогласования ε, нагрузкой q , производных и интегралов двух послед-

них величин называется алгоритмом регулятора, или законом регулирования.

Аналитически в общем виде:

yo	= ƒ (ε, ε', ε'', … t	ε dt,…q, q', q'',…).	(1.10)
	0

По виду этой функциональной зависимости и различают принципы регулирования.

Например, алгоритм регулятора по отклонению будет иметь зависимость:

		t
yo	= ƒ (ε,	ε', ε'', … ε dt).	(1.11)
		0
Алгоритм регулятора по нагрузке:
yo	= ƒ (q,	q', q'',…)	(1.12)

Уравнение (1.9) — алгоритм комбинированного регулирования.

Несколько конкретных алгоритмов регулирования:

— алгоритм пропорционального регулирования

y	= a0 · ε ,	(1.13)
o

где регулирующее воздействие пропорционально ε, и сами регулято-

ры называются П-регуляторами;

— алгоритм	регулирования	пропорциональный	с воздействием
по первой производной:
y	= а0 · ε + а1 · ε' ,		(1.14)
o
— алгоритм	регулирования	пропорциональный с воздействием
по первой и второй производной:
y	= а0 · ε + а1 · ε' + а2 · ε'',		(1.15)
o

— интегральный закон регулирования — И-регулятор:

t
yo = b0	ε dt,			(1.16)
0
— алгоритм регулирования пропорциональный с воздействием
по интегралу — ПИ-регулятор:
o		t
o
y = а0 ·	+ b0		ε dt	(1.17)
		0

1.1.4. Основные требования к автоматическим системам управления

Применение автоматического управления производственными процессами должно улучшать их технико-экономические показатели. Исключением являются случаи, когда основным и решающим фактором является улучшение труда обслуживающего персонала и если это обусловливается также соображениями техники безопасности.

Сформулированы общие требования к САУ:

максимальная простота, где не всегда необходима «полная автоматизация», т. е. системе поручают только те функции, которые совершенно необходимы;

САУ должна быть гибкой, т. е. допускать быстрый переход (в случае необходимости) к ручному управлению из нескольких мест;

САУ должна действовать как при нормальных, так и при аварийных режимах;

максимальная надежность САУ;

снижение стоимости автоматизированных установок;

применение типовых узлов, аппаратов и ряд др. Непосредственно к самой САУ все требования можно разбить

на следующие четыре категории:

требования к величине запаса устойчивости;

требования к величине отклонения регулируемого параметра в установившемся режиме (статическая точность);

требования к поведению системы в переходном процессе (качество переходного процесса);

требования к динамической точности системы, т. е. к величине отклонения при наличии непрерывно изменяющихся воздействий [42, 43].

1.2. Передаточные функции линейных систем. Структурные схемы и их преобразования

При исследовании САР широко используются структурные схемы, которые представляют собой условное графическое изображение дифференциального уравнения.

При составлении структурных схем каждое звено системы (группа звеньев) обозначается прямоугольником, в который вписывается его передаточная функция. При этом различают четыре основных типа дифференциальных уравнений [42, 43]:

1.	Звено с одной входной и одной выходной величиной (рис.
1.8); уравнением изображения этого звена будет:
				X (s) W (s)F(s) ,			(1.18)
ƒ				x		Рис. 1.8 — Звено с одной входной
		W(s)				Рис. 1.8 — Звено с одной входной
						и одной выходной величиной
						и одной выходной величиной

2.	Безинерционное звено с коэффициентом передачи К (рис.
1.9):
					x(t) Kf (t)		(1.19)
	ƒ				x	Рис. 1.9 — Безинерционное звено
	ƒ		К		x

3. Звено с двумя входными и одной выходной величиной (рис.

1.10):

			X (s) W (s)[F (s) F (s)]					(1.20)
					1	2		(1.20)
ƒ1	+		x	ƒ1	+			x
ƒ1		W(s)	x				W(s)	x
		W(s)					W(s)

ƒ2

Рис. 1.10 — Две формы представления звена с двумя входными

иодной выходной величиной

4.Звено с двумя передаточными функциями и двумя входными сигналами (рис. 1.11):

	X (s) W (s)F (s) W (s)F (s)					(1.21)
		1	1	2	2
	ƒ2			ƒ1
	ƒ2	x				W1(s)	x
						W1(s)
ƒ1	W2(s)
ƒ1	W2(s)
	W1(s)			ƒ		W2(s)
	W1(s)					W2(s)

Рис. 1.11 — Две формы представления звена с двумя передаточными функциями и двумя входными сигналами

Используя эти изображения, составляются структурные схемы. Пример структурной схемы ЭМУ в виде двух звеньев первого

порядка:

Uу

E′q

Uу

или

Рис. 1.12 — Структурная схема ЭМУ

Здесь:

1 у

;

2 q

K K

эму

rу

Для исследования системы необходимо знать ее передаточную функцию, для чего необходимо познакомиться с преобразованиями структурных схем.

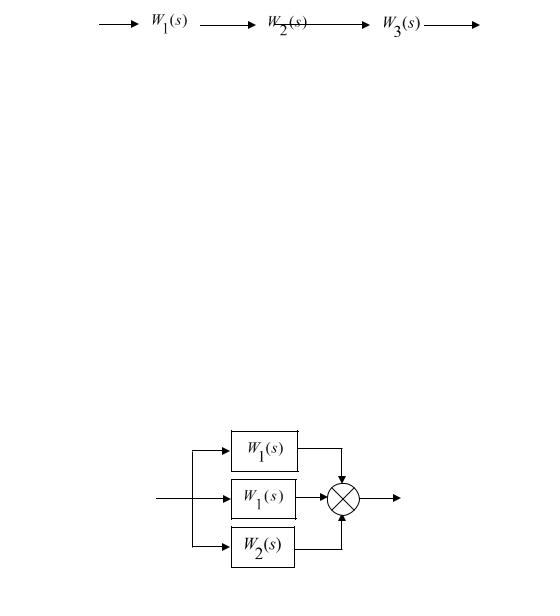
1. Последовательное соединение звеньев: вход каждого последу-

ющего звена соединяется с выходом предыдущего (рис. 1.13).

X1	Х2	Х3	Х4
X1	Х2	Х3	Х4

Рис. 1.13 — Последовательное соединение звеньев


X 2(s) W1(s) X1(s) ,			X3(s) W2(s)X2(s) ,	X4(s) W3(s)X3(s)
и	X4	(s) W1(s) W 2 (s) W3(s) X1(s) W (s) X1(s)			(1.22)
	X4	(s) W1(s) W 2 (s) W3(s) X1(s) W (s) X1(s)

Итак, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев:

	W (s) W1(s) W2(s) W3(s)		(1.23)
2. Параллельное соединение звеньев: входная величина одинакова
для звеньев, а выходные величины суммируются (рис. 1.14):
X1(s) W1(s) Xвх(s) ,	X2(s) W2(s) Xвх(s) ,	X3(s) W3(s) Xвх(s)	(1.24)
Уравнение сумматора:
Xвых(s) X1(s) X2(s) X3(s) [W1(s) W2(s) W3(s)] Xвх(s) .			(1.25)

		Х1
Х	вх	Хвых
	вх	Х2
		Х2
		Х3

Рис. 1.14 — Параллельное соединение трех звеньев

Передаточная функция:

W (s) W1(s) W2(s) W3(s) . (1.26)

Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций звеньев.

3. Охват звена обратной связью (рис. 1.15). Исходные уравне-

ния:	Xвых(s) Wо(s) X (s) ,	(1.27)
для охватываемого звена	Xвых(s) Wо(s) X (s) ,	(1.27)

для звена обратной связи	Xос(s) Wос(s) Xвых(s)	(1.28)
для сумматора	X (s) Xвх(s) Xос(s) ,	(1.29)

здесь знак «+» — для ПОС,	знак «–» — для ООС.

Хвх	Х′	Хвых
		Хвых

Хос

Рис. 1.15 — Охват звена обратной связью

В уравнениях исключаем промежуточные величины:


Xвых(s)		Wo(s)
		Wo	(s) Woc(s)
	1
и передаточная функция:W (s)		Wo(s)
	1 W (s) W (s)
		o	oc

Хв х(S)

(1.30)

. (1.31)

Основные правила преобразования структурных схем

1.Группу последовательного, параллельного соединения звеньев или охваченных обратной связью соединения звеньев можно заменить одним звеном с соответствующей передаточной функцией.

2.Точку приложения или съема воздействия можно переносить через одно или несколько звеньев, добавляя в преобразуемую цепь звено с такой

передаточной функцией, чтобы выходной сигнал этой цепи не изменился.

Пример преобразования структурной схемы системы с перекрестной обратной связью (опущен оператор s) показан на рисунке

1.16:

— для освобождения от перекрестной связи точка съема воздействия 1 переносится в точку 2 с добавлением в цепь обратной связи

(W5), звено с передаточной функцией W3 (в соответствии с правилом

2);

— находится передаточная функция звена W6 (последовательное соединение звеньев с передаточными функциями W3 и W5);

— находится передаточная функция звена W7 (охват звена с передаточной функцией W2 обратной связью — звено обратной связи с передаточной функцией W6);

— находится передаточная функция звена W8 (последовательное соединение звеньев с передаточными функциями W1 и W7);

— находится передаточная функция звена W9 (охват звена с передаточной функцией W8 обратной связью — звено обратной связи с передаточной функцией W4);

— находится передаточная функция звена W10 — системы (последовательное соединение звеньев с передаточными функциями W9

и W3) [42, 43].

Хвх	W1	2	1	Хвых
		W2	W3

W4 W5

Хвх		2		1
Хвх	W1	W	W	Хвых
		2	3

W3 W5

Хвх W1 W2 W3 Хвых

Хвх W1 W7 W3 Хвых

Хвх W8 W3 Хвых

Хвх

Хвых

Хвх	W	Х	вых	Рис. 1.16 — Пример преобразования

	10			структурной схемы

<<< < Предыдущая 1 23 / 373 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке Примеры построения схем автоматизации, в том числе, для колонн

#
06.06.20219.67 Mб2432012 [Беспалов] Системы управления ХТП.pdf
#
06.06.20217.18 Mб2752015 [Тынчеров] Основы автоматизации ТПНП.pdf