
литература / Примеры построения схем автоматизации, в том числе, для колонн / 2015 [Тынчеров] Основы автоматизации ТПНП
.pdf
Рис. 4.50 — Образование вихрей
Количество вихрей, генерируемое в секунду f от каждой стороны поверхности обтекаемого тела, можно определить как
(4.39)
где vs — средняя скорость жидкости вблизи плохо обтекаемого тела; S — фактически постоянная величина, называемая числом Струхаля. Поток жидкости тела протекает через площадь, равную
(4.40)
где D — диаметр трубы. Предполагается, что тело имеет прямоугольную поверхность поперечного сечения шириной d, расположенную в диаметральной плоскости трубы, и его эффективная площадь равна примерно Fd.
Скорость vs в этом месте определяется скоростью v на некотором удалении от тела, и объемный расход Q может быть определен как
(4.41)
следовательно,
(4.42)
Имеется много методов для измерения частоты вихрей. Например, можно измерять давление потока за обтекаемым телом. При возникновении вихря статическое давление уменьшается. Таким образом, по частоте изменения давления, измеряемого кварцевым пьезоэлементом, можно судить о частоте вихрей, а значит, и о расходе вещества.

В другом методе вихри оказывают воздействие на луч ультразвуковой волны. Этот метод реализован в вихреакустических расходомерах (рис. 4.51). Преобразователь в этом случае представляет собой моноблочную конструкцию, состоящую из проточной части и электронного блока. В корпусе проточной части расположены: тело обтекания — призма трапецеидального сечения 1, пьезоизлучатели (ПИ) 2, пьезоприемники (ПП) 3 и термодатчик 7.
Электронный блок включает в себя генератор 4, фазовый детектор 5, микропроцессорный адаптивный фильтр с блоком формирования выходных сигналов 6, смонтированные на печатной плате.
Рис. 4.51 — Вихреакустические расходомеры
Тело обтекания (ТО) установлено на входе жидкости в проточную часть. При обтекании ТО потоком жидкости за ним образуется вихревая дорожка, частота следования вихрей в которой с высокой точностью пропорциональна скорости потока, а следовательно, и расходу.
За ТО в корпусе проточной части диаметрально противоположно друг другу установлены стаканчики, в которых собраны ультразвуковой пьезоизлучатель (ПИ) и пьезоприемник (ПП).
В зависимости от типа преобразователи имеют два конструктивных исполнения:
1)однолучевые преобразователи — одна пара ПИ, ПП (Dу 25– 200 мм);
2)двухлучевые преобразователи — две пары ПИ, ПП (Dу 250– 300 мм).
От генератора на ПИ подается переменное напряжение, которое преобразуется в ультразвуковые колебания. При прохождении через поток в результате взаимодействия с вихрями ультразвуковые колебания модулируются по фазе. На ПП модулированные ультразвуковые колебания вновь преобразуются в напряжение, которое подается на фазовый детектор. На фазовом детекторе определяется разность фаз между сигналами с ПП и опорного генератора для однолучевых преобразователей.
Напряжение на выходе фазового детектора по частоте и амплитуде соответствует частоте и интенсивности следования вихрей, которая в силу пропорциональности скорости потока является мерой расхода.
Вихревые расходомеры применяются и для жидкостей, и для газов. Они не чувствительны к изменениям плотности, температуры или давления, имеют точность ±1% и используются при давлении до 10 МПа и температуре до 200°С [27].
4.5.8. Кориолисовы расходомеры
Законами механики установлено, что на массу m, движущуюся со скоростью относительно системы отсчета, находящейся во вра-
щательном движении с угловой скоростью , действует сила , называемая силой Кориолиса (Г. Кориолис (1792–1843) — французский физик).
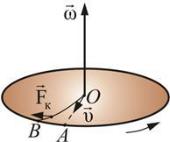
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 4.52).
Рис. 4.52 — Иллюстрация кориолисовой силы
Запустим в направлении от О к А шарик со скоростью . Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск
привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила fc , перпендикулярная направлению движения шарика.
Сила Кориолиса не является «настоящей» в смысле механики Ньютона. При рассмотрении движений относительно инерциальной системы отсчета такая сила вообще не существует. Она вводится искусственно при рассмотрении движений в системах отсчета, вращающихся относительно инерциальных, чтобы придать уравнениям движения в таких системах формально такой же вид, что и в инерциальных системах отсчета.
Чтобы заставить шарик катиться вдоль ОА, нужно сделать направляющую, выполненную в виде ребра. При качении шарика направляющее ребро действует на него с некоторой силой. Относительно вращающейся системы (диска) шарик движется с постоянной по направлению скоростью. Это можно объяснить тем, что эта сила уравновешивается приложенной к шарику силой инерции:
|
= 2 [ ], |
(4.43) |
|
|
|
где — масса; — скорость относительно принятой системы отсчета; — угловая скорость вращения диска.
Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид:
|
|
= 2[ ]. |
(4.44) |
|
|
|
Ускорение направлено перпендикулярно векторам , и максимально, если относительная скорость точки ортогональна угловой скорости вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами , равен нулю или π, либо если хотя бы один из этих векторов равен нулю.
Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу.
Таким образом, всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда те-

ло изменяет свое положение по отношению к вращающейся системе отсчета.
Эта закономерность является основой принципа действия расходомеров, схема датчика которых показана на рисунке 4.54.
Жидкость, массовый расход Q которой необходимо измерить, течет со скоростью v через измерительную трубку U-образной формы (4.53). Трубку приводят в колебательное движение относительно оси ОО', перпендикулярной рукавам U-образной трубки; мгновенная угловая скорость трубки равна W. При отсутствии расхода жидкости оба рукава трубки колеблются синфазно, т. е. угол Ɵ поворота трубки равен нулю. При ненулевом расходе жидкости возникает сила Кориолиса, которая действует на рукава трубки в разных направлениях, так как жидкость течет в них в разные стороны.
Рис. 4.53 — Чувствительный элемент кориолисовых расходомеров:
а— при отсутствии расхода; б — при наличии расхода;
в— вид на чувствительный элемент спереди при наличии расхода
Врезультате рукава колеблются со сдвигом по фазе. Величину этого сдвига можно определить по сигналам преобразователей перемещения, укрепленных на рукавах трубки. В расходомере «Метран360» для этой цели применяют индуктивные преобразователи перемещений.
А в качестве устройства возбуждения колебаний применяют электромагнит переменного тока. Колебания трубки происходят на ее собственной частоте, которая зависит от массы трубки вместе с находящейся в ней жидкостью. Так как объем трубки всегда постоянный, то масса трубки однозначно зависит от плотности заполняющей ее среды.
Таким образом, по частоте колебаний трубки можно определить плотность, находящейся в ней жидкости.

Рис. 4.54 — Внешний вид кориолисового расходомера «Метран-360»
Погрешность измерения расхода составляет 0,25%. Абсолютная погрешность измерения плотности составляет ±2…3 кг/м3. Недостатком таких расходомеров является высокая стоимость.
В России одним из основных производителей расходомеров подобного типа являются предприятия ПГ «Метран». На рисунке 4.54 показан внешний вид современного кориолисового расходомера
«Метран-360» [18].
Глава 5. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ВИБРАЦИИ
5.1. Методы измерения вибрации
Вибрация — это механические колебания тела.
Самый простой вид вибрации — это колебание или повторяющееся движение объекта около положения равновесия. Этот тип вибрации называется общей вибрацией, потому что тело перемещается как единое целое и все его части имеют одинаковую по величине и направлению скорость. Положением равновесия называют такое положение, в котором тело находится в состоянии покоя, или положение, которое оно займет, если сумма действующих на него сил равна нулю.
Колебательное движение твердого тела может быть полностью описано в виде комбинации шести простейших типов движения: по-
ступательного в трех взаимно перпендикулярных направлениях (х,
у, z в декартовых координатах) и вращательного относительно трех взаимно перпендикулярных осей (Ох, Оу, Оz). Любое сложное перемещение тела можно разложить на эти шесть составляющих. Поэтому о таких телах говорят, что они имеют шесть степеней свободы.
Например, корабль может перемещаться в направлении оси «корма — нос» (прямо по курсу), подниматься и опускаться вверхвниз, двигаться в направления оси «правый борт — левый борт», а также вращаться относительно вертикальной оси и испытывать бортовую и килевую качку.
Представим себе некий объект, перемещения которого ограничены одним направлением, например, маятник настенных часов. Та-
кая система называется системой с одной степенью свободы, т. к.
положение маятника в любой момент времени может быть определено одним параметром — углом в точке закрепления. Другим примером системы с одной степенью свободы является лифт, который может перемещаться только вверх и вниз вдоль ствола шахты.
Вибрация тела всегда вызывается какими-то силами возбуждения. Эти силы могут быть приложены к объекту извне или возникать внутри него самого. Далее мы увидим, что вибрация конкретного объекта полностью определяется силой возбуждения, ее направлением и частотой. Именно по этой причине вибрационный анализ позволяет выявить силы возбуждения при работе машины. Эти силы зави-

сят от состояния машины, и знание их характеристик и законов взаимодействия позволяет диагностировать дефекты последней.
Простейшее гармоническое колебание. Самыми простыми из существующих в природе колебательных движений являются упругие прямолинейные колебания тела на пружине (рис. 5.1).
Такая механическая система обладает одной степенью свободы. Если отвести тело на некоторое расстояние от положения равновесия и отпустить, то пружина вернет его в точку равновесия. Однако тело приобретет при этом определенную кинетическую энергию, проскочит точку равновесия и деформирует пружину в противоположном направлении. После этого скорость тела начнет уменьшаться, пока оно не остановится в другой крайней позиции, откуда сжатая или растянутая пружина опять начнет возвращать тело назад в положение равновесия. Такой процесс будет повторяться вновь и вновь, при этом происходит непрерывное перетекание энергии от тела (кинетическая энергия) к пружине (потенциальная энергия) и обратно.
Рис. 5.1 — Пример простейшего колебания
На рисунке 5.1 представлен также график зависимости перемещения тела от времени. Если бы в системе отсутствовало трение, то эти колебания продолжались бы непрерывно и бесконечно долго с постоянными амплитудой и частотой. В реальных механических системах такие идеальные гармонические движения не встречаются. Любая реальная система обладает трением, которое приводит к постепенному затуханию амплитуды и превращает энергию колебаний в тепло. Простейшее гармоническое перемещение описывается следующими параметрами: Т — период колебаний, F — частота колебаний = 1/Т.
Период колебаний — это интервал времени, который необходим для завершения одного цикла колебания, то есть это время между двумя последовательными моментами пересечения нулевой точки
в одном направлении. В зависимости от быстроты колебаний период измеряют в секундах или миллисекундах.
Частота колебаний — величина обратная периоду, определяет количество циклов колебания за период, она измеряется в герцах (1 Гц = 1/секунду). Когда рассматриваются вращающиеся машины, то частота основного колебания соответствует частоте вращения, кото-
рая измеряется в об/мин (1/мин) и определяется как: |
|
= F∙ 60, |
(5.1) |
где F — частота в Гц, т. к. в минуте 60 секунд.
Уравнения колебаний. Если по вертикальной оси графика отложить положение (смещение) объекта, испытывающего простые гармонические колебания, а по горизонтальной шкале — время (рис. 5.1), то результатом будет синусоида, описываемая уравнением:
D = D sin(ω t), |
(5.2) |
где d — мгновенное смещение; D — максимальное смещение; ω = 2 F — угловая (циклическая) частота, = 3,14.
Это та самая синусоидальная кривая, которая всем хорошо известна из тригонометрии. Ее можно считать простейшей и основной временной реализацией вибрации. В математике функция синуса описывает зависимость отношения катета к гипотенузе от величины противолежащего угла. Синусоидальная кривая при таком подходе является просто графиком синуса в зависимости от величины угла. В теории вибраций синусоидальная волна также является функцией времени, однако один цикл колебания иногда рассматривают так же, как изменение фазы на 360 градусов. Об этом мы еще поговорим подробнее при рассмотрении понятия фазы.
Упомянутая выше скорость движения определяет быстроту изменения положения тела. Скорость (или быстрота) изменения некоторой величины относительно времени, как известно из математики, определяется производной по времени:
V = dn/dt = Dcos(ω t), |
(5.3) |
где n — мгновенная скорость.
Из этой формулы видно, что скорость при гармоническом колебании также ведет себя по синусоидальному закону, однако вследствие дифференцирования и превращения синуса в косинус скорость
сдвинута по фазе на 90° (то есть на четверть цикла) относительно смещения.
Ускорение — это скорость изменения скорости:
a = dV /dt = ω –2 Dsin(ω t), |
(5.4) |
где а — мгновенное ускорение.
Следует отметить, что ускорение сдвинуто по фазе еще на 90 градусов, на что указывает отрицательный синус (то есть на 180 градусов относительно смещения).
Из приведенных уравнений видно, что скорость пропорциональна смещению, умноженному на частоту, а ускорение — смещению, умноженному на квадрат частоты.
Это означает, что большие смещения на высоких частотах должны сопровождаться очень большими скоростями и чрезвычайно большими ускорениями. Представьте, например, вибрирующий объект, который испытывает смещение 1 мм с частотой 100 Гц. Максимальная скорость такого колебания будет равна смещению, умноженному на частоту:
V = 1*100 = 100 мм/с. |
(5.5) |
Ускорение равно смещению, умноженному на квадрат частоты,
или
а = 1 ∙ (100)2 = 10000 мм с2 = 10 м/с2. |
(5.6) |
Ускорение свободного падения g равно 9,81 м/с2. Поэтому в единицах g полученное выше ускорение приблизительно равно
10/9,811 g.
Теперь посмотрим, что произойдет, если мы увеличим частоту до 1000 Гц:
V = 1 ∙ 1000 = 1000 мм/с = 1 м/с, |
|
а = 1 ∙ (1000)2 = 1000000 мм/с2 = 1000 м/с2 = 100 g. |
(5.7) |
Таким образом, мы видим, что высокие частоты не могут сопровождаться большими смещениями, поскольку возникающие в этом случае огромные ускорения вызовут разрушение системы.
