Федеральное агентство связи ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет инфокоммуникационных сетей и систем Кафедра программной инженерии и вычислительной техники

ЛАБОРАТОРНАЯ РАБОТА №4 по дисциплине «Системы искусственного интеллекта»

Выполнил: студент 3-го курса дневного отделения группы ИКПИ-85

Коваленко Леонид Александрович Преподаватель:

доцент кафедры ПИиВТ Белая Татьяна Иоанновна

Санкт-Петербург

2021

Цель работы Изучение модели слоя Кохонена и алгоритма обучения без учителя;

создание и исследование модели слоя Кохонена.

Задание Индивидуальное задание согласно варианту представлено в табл. 1.

Таблица 1 — Индивидуальное задание

Теоретические сведения

Обучение без учителя (Unsupervised learning) — один из разделов машинного обучения. Изучает широкий класс задач обработки данных, в которых известны только описания множества объектов (обучающей выборки), и требуется обнаружить внутренние взаимосвязи, зависимости, закономерности, существующие между объектами.

Нейронные сети Кохонена — класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «Победитель получает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.

Важным недостатком является то, что окончательный результат работы нейронной сети зависит от начальных установок. С другой стороны, нейронная сеть теоретически может аппроксимировать любую непрерывную функцию, что позволяет исследователю не принимать заранее какие-либо гипотезы относительно модели.

1Номера классов в таблице наведены условно.

2

Практическая часть Проверочные точки представлены в табл. 2.

Таблица 2 — Проверочные точки

нейронной сети, на языке MATLAB с использованием функций Neural Network Toolbox представлен в табл. 4.

3

Таблица 4 — Код на MATLAB (Neural Network Toolbox)

program1.m

%Для MATLAB R2018b (9.5.0.944444) Pro

%Программа, написанная с использованием функций Neural Network Toolbox clear all; close all; clc;

%=== Исходные данные ===

%Обучающая выборка из 15 точек

%Маркеры классов обучающей выборки (по классам) training_markers = ['*r'; 'xr'; 'sr'; 'dr'];

%Маркеры классов проверочной выборки (по классам) test_markers = ['*b'; 'xb'; 'sb'; 'db'];

%Минимальные и максимальные значения координат min_c = min([-10, P(1, :), P(2, :)]);

max_c = max([+10, P(1, :), P(2, :)]);

%=== Построение нейронной сети Кохонена ===

%Диапазон значений входов: от -10 до 10; 4 класса net = newc([min_c max_c; min_c max_c], 4);

%Установка макс. количества эпох для обучения: 100 net.trainParam.epochs = 100;

%Обучение сети

net = train(net, P);

W = net.IW{1}; % Матрица весов

% Моделирование работы нейронной сети на проверочной выборке a = sim(net, A);

%Визуализация полученного результата figure(1); % Создание окна номер 1 с фигурой

hold on; % Отключение удаления старых графиков при создании новых в том же окне p = sim(net, P); % Моделирование работы на обучающей выборке

plot_sim_p(P, p, training_markers); % Построение обучающей выборки plot(W(1, 1), W(1, 2), center_markers(1, :)); % Центр класса номер 1 plot(W(2, 1), W(2, 2), center_markers(2, :)); % Центр класса номер 2 plot(W(3, 1), W(3, 2), center_markers(3, :)); % Центр класса номер 3 plot(W(4, 1), W(4, 2), center_markers(4, :)); % Центр класса номер 4 plot_sim_p(A, a, test_markers); % Построение проверочной выборки

axis([(min_c + 2) (max_c + 2) (min_c + 2) (max_c + 2)]); % Настройка диапазонов осей графика

xlabel('X'); ylabel('Y'); grid on;

%Функция построения точек p согласно указанным в sim_p классам

%и стилем, задаваемым markers

function [] = plot_sim_p(p, sim_p, markers) for i=1:size(sim_p, 2)

for j=1:size(sim_p, 1) if (sim_p(j, i) == 1)

plot(p(1, i), p(2, i), markers(j, :)); break;

end

end

end

end

Результат запуска программы представлен на рис. 1, 2, 3.

4

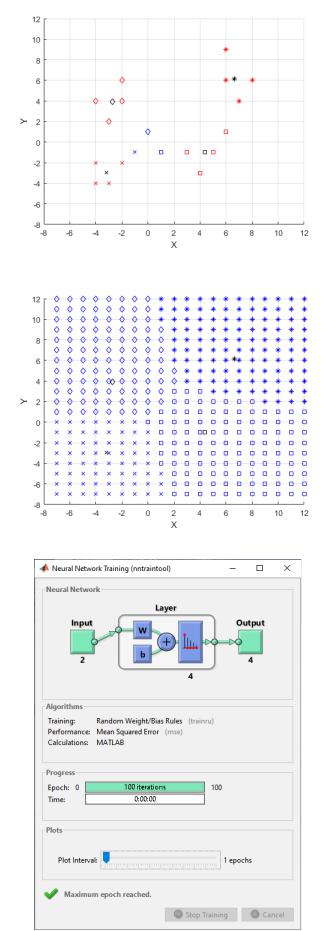
Рисунок 1 — Общая классификация

Рисунок 2 — Классификация сетки точек

Рисунок 3 — Процесс обучения в MATLAB

5

Код программы, моделирующей, обучающей и тестирующей работу нейронной сети, на языке Python с использованием библиотеки Neurolab представлен в табл. 5.

Таблица 5 — Код на Python (Neurolab)

program2.py

"""

Python 3.8.8 (tags/v3.8.8:024d805, Feb 19 2021, 13:18:16) [MSC v.1928 64 bit (AMD64)] on win32

-neurolab version is 0.3.5

-matplotlib version is 3.3.4

-numpy version is 1.19.5

"""

import neurolab as nl import numpy as np

from matplotlib import pyplot

#=== Исходные данные ===

#Обучающая выборка из 15 точек

X = np.array([3, 5, 4, 6, -4, -2, -4, -3, 6, 6, 8, 7, -2, -4, -2, -3], float)

Y = np.array([-1, -1, -3, 1, -2, -2, -4, -4, 9, 6, 6, 4, 6, 4, 4, 2], float) P = np.c_[X, Y]

# Проверочная выборка (14 вариант)

A = np.array([[0, 1, -1], [1, -1, -1]], float)

Axy = list(zip(*A))

#Axy = [[x, y] for x in range(-8, 12 + 1) for y in range(-8, 12 + 1)]

#Маркеры центров классов

center_markers = ['k*', 'kx', 'ks', 'kd']

#Маркеры классов обучающей выборки (по классам) training_markers = ['r*', 'rx', 'rs', 'rd']

#Маркеры классов проверочной выборки (по классам) test_markers = ['b*', 'bx', 'bs', 'bd']

#Минимальные и максимальные значения координат min_c = min([-10, min(X), min(Y)])

max_c = max([+10, max(X), max(Y)])

#=== Построение нейронной сети Кохонена ===

#Диапазон значений входов: от -10 до 10; 4 класса

net = nl.net.newc([[min_c, max_c], [min_c, max_c]], 4)

#Обучение сети

error = net.train(P, epochs=200, show=0)[-1]

while error > 34: # До тех пор, пока ошибка не будет приемлемой2 error = net.train(P, epochs=200, show=0)[-1]

W = net.layers[0].np['w'] # Матрица весов

#Моделирование работы нейронной сети на проверочной выборке a = net.sim(Axy)

#Визуализация полученного результата

pyplot.figure(figsize=(5, 5), dpi=90) # Создание нового окна с графиком

#Функция построения точек p согласно указанным в sim_p классам

#и стилем, задаваемым markers

def plot_sim_p(p, sim_p, markers): for i in range(sim_p.shape[0]):

for j in range(sim_p.shape[1]): if sim_p[i][j] == 1:

pyplot.plot(p[i][0], p[i][1], markers[j]) break

2Результат работы зависит от начальных установок сети. Итоговая ошибка обычно варьируется от 33 до 60.

6

pyplot.ylabel('Y') pyplot.grid() pyplot.show()

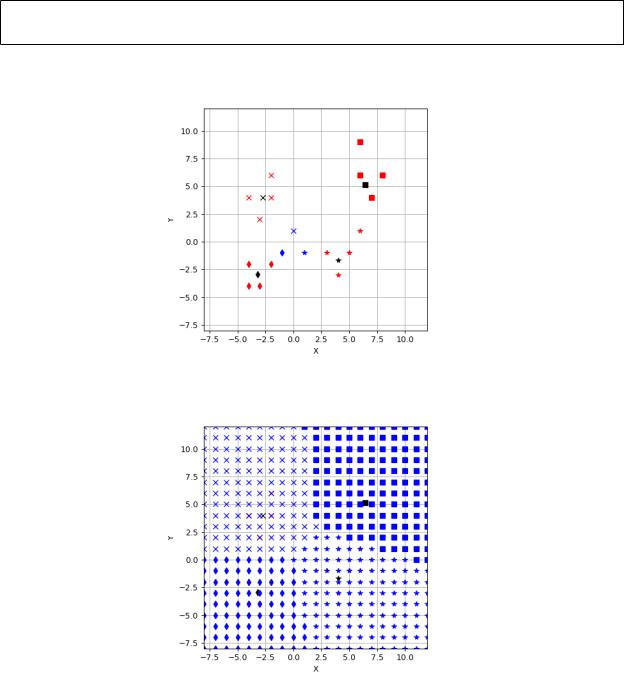
Результат запуска программы представлен на рис. 4, 5.

Рисунок 4 — Общая классификация

Рисунок 5 — Классификация сетки точек

Заключение В результате выполнения лабораторной работы мы изучили модель

слоя Кохонена и алгоритм обучения без учителя; создали и исследовали модель слоя Кохонена в системе MATLAB и с использованием языка программирования Python с библиотекой Neurolab.

Применение функций пакета Neural Network Toolbox существенно упрощает построение, обучение и использование ИНС.

7