дз2

Министерство науки и высшего образования Российской Федерации

Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Московский государственный технический университет имени Н.Э. Баумана

(Национальный Исследовательский Университет)»

(КФ МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ	М-КФ «Машиностроительный»
КАФЕДРА	М10-КФ «Высшая математика»

ДОМАШНЯЯ РАБОТА №2

ДИСЦИПЛИНА:	«Теория вероятностей и математическая статистика»
ТЕМА:	«Основные понятия математической статистики»

Выполнил: студент гр. ИУК1-41Б	_______________(Прудников А.Ф.) Подпись Ф.И.О.
Проверил:	_______________(Савотин А.И.) Подпись Ф.И.О.

Дата сдачи (защиты):
Результаты сдачи (защиты): -Балльная оценка -Оценка

Калуга, 2021 г.

Задание №1

Рассчитать и построить гистограмму относительных частот по группированным данным (таблица 1), где – частота попадания вариант в промежуток .

Решение:

i
1	10-12	4
2	12-14	12
3	14-16	8
4	16-18	8
5	18-20	18
∑	m	50

таблица 1

Вычислим по формуле :

i
1
2
3
4
5

Постороим график в виде гистограммы, в котором ось OX это , а ось OY это :

Задание №2

Найти несмещенную выборочную дисперсию на основании данного распределения выборки (таблица 2).

Решение:

	-3	1	4	8
	2	3	1	4

таблица 2

Найдём сумму всех частот :

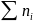Найдём выборочную среднюю:

;

Выборочная дисперсия:

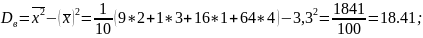
Найдём несмещенную выборочную дисперсию:

Ответ:

Задание №3

Проверить нулевую гипотезу о том, что заданное значение является математическим ожиданием нормального распределения случайной величины при 5%-м уровне значимости для двухсторонней критической области, если в результате обработки выборки объема получено выборочное среднее x, а выборочное среднее квадратичное равно (табл. 3).

Решение:

	x
100	96	6

таблица 3

1. ;

;

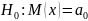2. Уровень значимости:

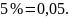
3. Критерий проверки , откуда .

4. Данная гипотеза 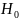имеет распределение Стьюдента. По таблице распределений находим :

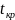в 9ой тройке, т.к. и в столбце 0,025, т.к.

.

5. Двухсторонняя критическая область , т.е.

6. , значит, гипотеза математическое ожидание равно принимается.

Ответ: Нулевая гипотеза принимается.

Задание №4

При уровне значимости проверить гипотезу о равенстве дисперсии двух нормально расположенных слуайных величин X и Y на основе выборочных данных (табл. 4) при альтернативной гипотезе 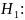дисперсии не равны .

Решение:

X		Y
42	15	84	3
45	17	87	2
46	12	92	4
50	16	96	1

таблица 4

1. 

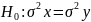
2. – уровень значимости.

3. Критерий проверки:

, если .

, если .

Отсюда находим .

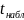4. Данная гипотеза о равенстве дисперсий имеет распределение Фишера из таблица распределения Фишера находится . В столбце и строке для для . А если , то в столбце и строке .

5. 

   1. 

   2. ;

   3. .

1. 

2. ;

3. .

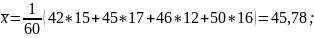
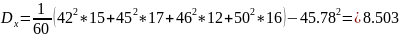Т.к. , то значение по следующей формуле:

6. находится в столбце и строке . .

7. 

8. Данная гипотеза не принимается, т.к. . не принимается.

Ответ: не принимается.

Задание №5

Найти выборочное уравнение линейной регрессии Y на X на основании корреляционной таблицы (табл. 5).

Решение:

таблица 5

1. Составим таблицу для упрощения расчётов. Вводятся условные варианты:

В данном случае 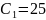, , , . Т.о. формулы примут следующий вид:

2. Таблица условных вариант:

таблица 5.1

3. Составим расчётную таблицу:

таблица 5.2

4. По таблице условных вариант находим числовые характеристики:

;

;

;

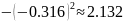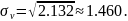
5. Вычислим коэффициент корреляции:

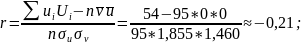
6. Переходим к исходным вариантам по формулам:

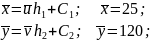
7. Нахождение коэффициента линейной регрессии:

Уравнение регрессии:

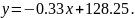
Ответ:

Задание №6

При уровне значимости методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объектов на основании пяти измерений для трёх уровней факторов (табл. 6).

Р ешение:

таблица 6.1

– рассматриваемый фактор существенно влияет на качество объекта.

– рассматриваемый фактор влияет несущественно на качество объекта.

Для проверки гипотезы необходимо произвести следующие вычисления:

1. Найти групповые средние:

Каждая групповая средняя:

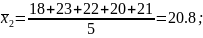
2. Общее среднее:

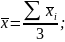
3. Составим таблицу квадратов:

4. Найдём общую сумму квадратов отклонения от общей средней:

5. Найдём факторную сумму квадратов отклонений от границы средней x:

6. Найдём остаточную сумму квадратов отклонений:

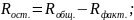
7. Найдём фактическую дисперсию:

8. Найдём остаточную дисперсию:

9. Найдём наблюдаемое значение:

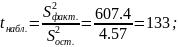
10. Найдём критическое значение по табл. Фишера при значимости при пересеччении столбца и строки .

Т.к. , то гипотеза принимается.

Ответ: Рассматриваемый фактор существенно влияет на качество объекта.