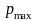лр2
.docx
|
Министерство науки и высшего образования Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)» (КФ МГТУ им. Н.Э. Баумана) |
ФАКУЛЬТЕТ |
ИУК «Информатика и управление»____________ |
КАФЕДРА |
ИУК1 «Проектирование и технология производства электронных приборов»_______ |
лабораторная работа № 2
«ФОРМИРОВАНИЕ БИПОЛЯРНОГО ТРАНЗИСТОРА С ПОМОЩЬЮ ДИФФУЗИИ»
ДИСЦИПЛИНА: «ФИЗИЧЕСКИЕ ОСНОВЫ МИКРОЭЛЕКТРОНИКИ»
Выполнил: студент гр. ИУК1-41Б |
_______________ (Прудников А.Ф.) (Подпись) (Ф.И.О.)
|
Проверил: |
_______________ (_Шагаев В.В.__) |
(Подпись) (Ф.И.О.)
Дата сдачи (защиты):
Результаты сдачи (защиты):
- Балльная оценка:
- Оценка:
Калуга, 2021 г.
Лабораторная работа №2
Моделирование энергетического спектра электрона в твердом теле (модель Кронига-Пенни)
Цель: формирование навыков расчета энергетического спектра электрона в периодическом потенциале.
Задачи: построить модель состояний электрона в одномерном периодическом потенциале с прямоугольными барьерами.
Вариант № 3.
№ варианта |
|
|
|
|
|
Результаты:
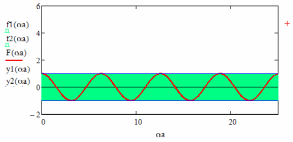
Рис.
1. Графический анализ условия
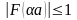в модели Кронига-Пенни, где
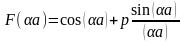с
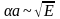и
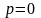– случай свободных
электронов;
заштрихованная область – область
допустимых значений функции и её
аргумента: ограничений на значения
энергии нет
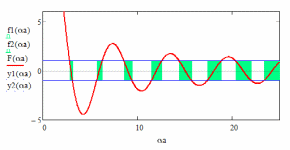
Рис.
2. Графический анализ условия
в модели Кронига-Пенни, где
с
и
;
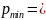заштрихованные области – области
допустимых значений функции и её
аргумента: разрешенные значения энергии
разбиты на зоны
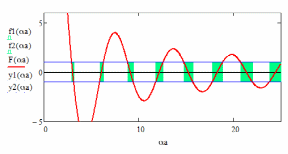
Рис. 3. Графический анализ условия в модели Кронига-Пенни, где с и ; заштрихованные области – области допустимых значений функции и её аргумента: разрешенные значения энергии разбиты на узкие зоны
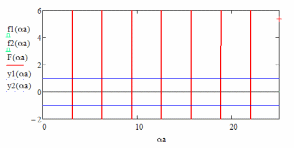
Рис.
4. Графический анализ условия
в модели Кронига-Пенни, где
с
и
– случай непрозрачных барьеров;
допустимые значения энергии ограничены
дискретным набором значений
Вывод: Сформировал навыки расчета энергетического спектра электрона в периодическом потенциале. Построили модель состояний электрона в одномерном периодическом потенциале с прямоугольными барьерами.
Контрольные вопросы
Сформулируйте граничные условия для волновой функции.
Граничные условия для волновой функции будут непрерывная волновая функция и её первая производная на границах А и В:
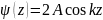
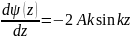
Какое свойство волновой функции обусловлено периодичностью потенциала?
Волновые законы движения электронов в периодическом потенциальном поле приводят к возникновению разрешенных и запрещенных зон энергии.
В каком виде энергия электрона входит в уравнение (4)?
В
уравнении (4) энергия электрона
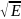заменяется на экивалентное значение
,
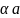где а
–
ширина потенциальной ямы, а
.
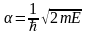Как ширина разрешенных зон зависит от параметров, характеризующих барьеры (от высоты и ширины)?
Уменьшение высоты и толщины барьера, вследствие сближения атомов может привести к тому, что барьер окажется прозрачным для туннелирования электронов.