Теория вероятности и математическая статистика / Теория вероятности, подготовка
.docxТеория вероятности
Основы комбинаторики. Предмет и задачи теории вероятностей. Пространство элементарных исходов. Алгебра событий.
Комбинаторика - нахождение числа всех способов расположения / выполнения
Соединения:
Перестановка
Сочетания
Размещения
Множество М из n элементов называется упорядоченным
Перестановка - упорядочения множества М из n элементов
«Сколькими способами можно переставить n объектов»
Без повторений
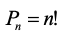
![]()
![]()

С повторениями
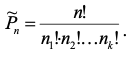

Сочетание (выборка) - набор элементов, рассматриваемых без учета порядка их следования (из n по k (k < n). Выбрать k предметов из n в точности = С.
«сколькими способами можно выбрать m объектов из n»
Порядок не важен
без повторений

![]()
с повторениями
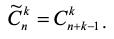
![]()


Размещение - Упорядоченное k-элементное подмножество множества М из n (без повторений)
«сколькими способами можно выбрать m объектов и в каждой выборке переставить их местами»
без повторений
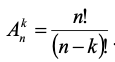
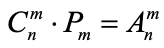
 с
повторениями
с
повторениями
![]()

Выбор с возвращением
![]()
Выбор без возвращения
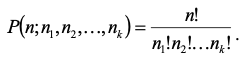
Теория вероятности – вероятностные закономерности массовых однородных случайных событий.
Виды событий:
Достоверное – обязательно произойдет
Невозможное – заведомо не произойдет
Случайное –p есть следствие случайных факторов
Случай / исход – любой результат испытания
Равновозможные события – ни одно из событий не является более возможным
События могут быть:
Совместные - появление одного, не исключает появление другого
Несовместные – если появление одного, исключает появление остальных
Противоположное
Полная группа событий – множество несовместных событий
Элементарность – то событие, которое нельзя разложить на другие
Сложение событий = ИЛИ
Умножение событий = И
Равновозможные – события вероятность которых одинакова
положительные / благоприятный исходы (p)
отрицательные исходы (q)
Диапазон измерения вероятности 0-1 (0 – 100%)
Основные понятия и определения. Классическое, статистическое и геометрическое определение вероятности
Классическая (написание всех возможных исходов)
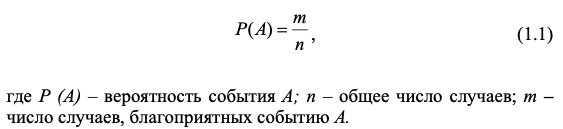
Основные теоремы теории вероятностей
Сложение (несовместные) - А + В = С, состоящее в выполнении события А или события В, или обоих вместе
Чтобы применить несовместные
![]()
Все события А1, А2, Аn – образуют полную группу, которая = 1
Сумма вероятностей А1 и противоположной -А1 = 1 (полная группа)
Независимое - одно событие не зависит от того, что произошло ли предыдущее
Зависимое - одно событие зависит от того, что произошло ли предыдущее
Умножение (совместные) - А * В = С, состоящее в совместном выполнении события А и события В
![]()
![]()
Оба события зависят друг от друга
Произведение 2-х независимых событий
![]()
Противоположные события - два несовместных события, образующих полную группу (попадание и промах)
Формула Байеса:
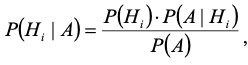
где Р(А) – полная вероятность события А
Формула Бернулли
Подразумевает выполнение 4-х условий:
кол-во повторных испытаний
независимые исп
исход «Успех» или «Неудача»
Вероятность «Успеха» постоянна
n – кол-во независимых испытаний
k – кол-во исп когда наступает событие А
Вероятность получения наивероятнейшего числа
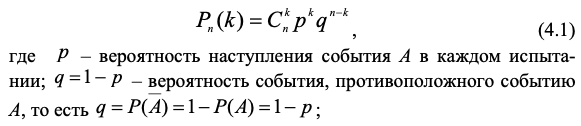
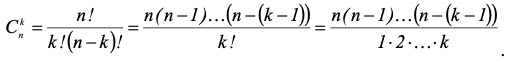 Наивероятнейшее
число
Наивероятнейшее
число
![]()
Случайной величины их распределения и числовые характеристики
Дискретное и непрерывной случайной величины. Закон распределения дискретной случайной величины
Случайная величина - переменная величина, которая в зависимости от исходов испытания и принимает значения, зависящие от случая. Результат – некоторое число
Дискретная случайная величина может принимать различные значения, которые можно записать виде конечной или бесконечной последовательности
Непрерывная случайная величина та, которая может принимать все значение из некоторого промежутка
Закон распределения дискретной случайной величины - это соответствия между возможными значениями и соответствующими им вероятностями
Задается:
таблично
аналитически (формула)
Сумма вероятностей = 1
Плотность распределения непрерывной случайной величины
Типы задач:
Построение закона (ряда) распределения (для прерывной случайной величины)
Введение и четкое описание случайной величины в задаче
описание множества и возможных значений
рассмотрение и выполнения каждого из неравенств, как случайного события
вычисление вероятностей этих событий с помощью основных теорем и формул
проверка правильности составленного распределения с помощью равенства = 1
Математическое ожидание
Для дискретной
(интегральная) Функция / закон распределения – существует для прерывных и непрерывных случайных величин. Она характеризует случайную величину со стороны вероятности.
Общие свойства:
Неубывающая
при –∞ = 0
при +∞ = 1
Для дискретной случайной величины
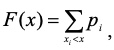
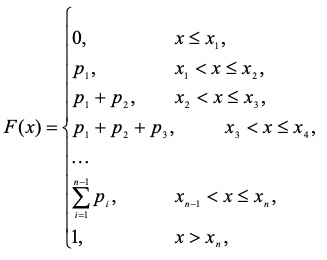

Плотность распределения - производная функции распределения. Существует для непрерывных случайных величин.
Свойства:
неотрицательная функция
интеграл с бесконечными пределами от плотности распределения = 1
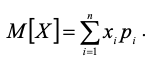
Непрерывной
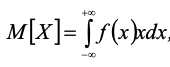
Мода
Для дискретной - ее наиболее вероятное значение
Непрерывной - значение, в котором плотность вероятности максимальна
Медиана случайной величины (характеристика для непрерывной величины) - это когда случайная величина меньше или больше Me
![]()
Дисперсия
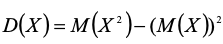
Среднее квадратичное отклонение / стандартное отклонение