Математика

Основная задача дифференциального исчисления @3. Нахождения производной по заданной функции.

ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ ФУНКЦИИ @1. Скорость изменения функции относительно её аргумента.

Геометрический смысл производной функции @3. Тангенс угла наклона касательной к кривой у=f(х).

н айдите уравнение скорости, если уравнение перемещения движения тела имеет вид @1. v=4t+1

В ТОЧКЕ Х=2,5 НАЙДИТЕ ПРОИЗВОДНУЮ ФУНКЦИИ

@ 2. 1

В ТОЧКЕ Х=3 НАЙДИТЕ ПРОИЗВОДНУЮ ФУНКЦИИ

@ 3. 7

Р АССЧИТАТЬ МГНОВЕННУЮ СКОРОСТЬ ДВИЖЕНИЯ ТОЧКИ В МОМЕНТ ВРЕМЕНИ t = 1с, ТОЧКА ДВИЖЕТСЯ ПРЯМОЛИНЕЙНО ПО ЗАКОНУ

@ 3. 10

Н АЙТИ СКОРОСТЬ ТОЧКИ В МОМЕНТ t= 1с , ЕСЛИ ТОЧКА ДВИЖЕТСЯ ПО ЗАКОНУ

@2. 10 м/с

НАХОЖДЕНИЕ ПРОИЗВОДНОЙ ПО ЗАДАННОЙ ФУНКЦИИ – ЭТО ОСНОВНАЯ ЗАДАЧА @1. Дифференциального исчисления

Р АССЧИТАТЬ СКОРОСТЬ ДВИЖЕНИЯ ТОЧКИ В МОМЕНТ t=1 с, ЕСЛИ ТОЧКА ДВИЖЕТСЯ ПО ЗАКОНУ

@4. 4 м/с.

@3. Дифференциал функции

В ТОЧКЕ Х=2 ВЫЧИСЛИТЕ ПРОИЗВОДНУЮ ФУНКЦИИ

@1. 20

Найдите производную функции f(x)=3-2x 

@2. -2

Н айдите производную функции

@4. -3sin3x+2x

Значение производной функции равно угловому коэффициенту касательной к графику функции y=f(x) в точке с абсциссой х, в этом заключается

@ 3. Геометрический смысл производной

Дифференцируя функцию скорости тела в механике получим

@ 3. Ускорение

Найдите производную функции

@ 2. 14x+2

Найдите производную функции

@3. 2x-3

Раздел математического анализа, связанный с понятиями производной и дифференциала функции называется

@4. Дифференциальное исчисление

Вычислите производную функцию f(х)=6х-5

@4. 6

Производная постоянной величины равна:

@2.0

Центральные понятия дифференциального исчисления:

@4. Производная и дифференциал

О сновнАЯ задачА интегрального исчисления @ 2. Отыскания функции по ее производной.

@ 3. х + С.

Геометрический смысл неопределенного интеграла @1. Семейство кривых

Геометрический смысл определенного интеграла @2. Площадь криволинейной трапеции.

Найдите первообразную функции f(x)=9

@4. 9х

Найдите первообразную функции  f(х) = sinx  и выберите один правильный ответ:

@2. -cosx

Неопределенным интегралом функции f(x) называется совокупность всех  её

@4. первообразных

Пределы интегрирования  а и в в определенном интеграле  соответственно называют

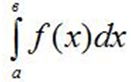
@4. Нижним и верхним

Определённый интеграл вычисляется по формуле

@3. Ньютона-Лейбница

Раздел математического  анализа, в  котором изучаются интегралы, их  свойства, способы вычисления и приложения называется

@2. Интегральное исчисление

Числовое значение площади криволинейной трапеции может быть

@2.Только положительное

Найдите первообразную функции f(х)=6

@1. 6x+C

Центральные понятия интегрального исчисления:

@4.Неопределённый и определённый интеграл

Случайным событием не является @3)восход Солнца

Вероятность случайного события @3)0< Р<1

Слово «дифференциал». Из него наугад выбирается одна буква. Вероятность того, что эта буква будет «ч», равна @3)0

Слово «дифференциал». Наугад выбирается одна буква. Вероятность того, что эта буква будет согласной равна @1)7/12

Частота нормального всхода семян w = 0,97. Из высеянных семян взошло 970. Было высеяно семян @2)1000

Вероятность невозможного события

@1)Р=0

515 мальчиков оказалось среди 1000 новорожденных. Частота рождения мальчиков равна @3)0,515

Вероятность достоверного события @2)Р=1

Поступило 982 больных в хирургическую клинику за месяц. 491 человек имели травмы. Относительная частота поступления больных с этим видом заболевания равна @3)0,5

Слово «дифференциал». Наугад выбирается одна буква. Вероятность того, что эта буква будет гласной равна @3)5/12

Бросают игральную кость. Возможны шесть исходов – выпадение 1,2,3,4,5,6 очков. Вероятность появления четного числа очков равна

@4)½

10 шаров в урне: 3 белых и 7 черных. Из нее наугад извлекают один шар. Вероятность, что этот шар будет белый, равна… @3)3/10

Победитель соревнования награждается призом (событие A), денежной премией (событие B), медалью (событие C). Событие A+B представляет собой награждение

@4)возможны все варианты

Турист имеет возможность посетить 3 города: А (событие А), В – событие В и С – событие С. Событие А+С представляет собой посещение

@4)возможны все варианты

Победитель соревнования награждается призом (событие А), денежной премией (событие В), медалью (событие С). Произведение событий АВ представляет собой награждение

@1)приз и денежная премия, но без медали

Пусть имеются следующие события: А – «из колоды карт вынута «дама»; В – « из колоды карт вынута карта пиковой масти». Произведение событий АВ - это

@3)пиковая дама

Закон сложения вероятностей для двух несовместных событий имеет вид

@1)Р(АилиВ)=Р(А)+Р(В)

Закон сложения вероятностей для двух совместных событий @2)Р(АилиВ)=Р(А)+Р(В)-Р(А)·Р(В)

Закон умножения вероятностей для двух независимых событий

@3)Р(АиВ)=Р(А)·Р(В)

Закон умножения вероятностей для двух зависимых событий

@4)Р(АиВ)=Р(А)·P(В/А)

Условная вероятность случайного события обозначается @2)P(B/A)

Дискретная случайная величина

@3)артериальное давление пациента в течение суток

К характеристикам случайных величин не относится

@1)вероятность

Распределение – это совокупность значений

@1)случайной величины и вероятностей их появления

Дискретная случайная величина Х имеет закон распределения, заданный таблицей. Вероятность Р₄ (Х=0,8) равна

Х 0 ,2 0,4 0,6 0,8 1,0 Р 0,1 0,2 0,4 Р₄ 0,1 @2) 0,2

Нормальный закон распределения используется для случайных величин

@1)непрерывных

Дифференциальная функция распределения вероятности f(x) всегда

@3)f(x)³0

Раздел математики, разрабатывающий методы систематизации данных, отыскания законов распределения случайных величин и их числовых характеристик, называется

@1) математическая статистика

Множество всех мыслимых значений наблюдений (объектов), однородных относительно некоторого признака, которые могли быть сделаны, называется

@2) генеральная совокупность

Совокупность случайно отобранных наблюдений (объектов) для непосредственного изучения называется

@1) выборка

Объем генеральной совокупности обозначается

@4) N

Объем выборки обозначается

@1) n

Выборка, дающая обоснованное представление о генеральной совокупности, называется

@3) репрезентативной

Совокупность вариант, расположенных в порядке возрастания, и соответствующих им частот, называется

@3) вариационный ряд

Из перечисленного характеристикой положения не является

@3) дисперсия

Из перечисленного характеристикой положения является

@2) среднее выборочное

Наиболее часто встречающаяся варианта в данной совокупности

@1) мода

Варианта, относительно которой вариационный ряд делится на две равные по объему части

@3) медиана

Среднее арифметическое значение вариант статистического ряда

@2) среднее выборочное

Среднее арифметическое квадратов отклонения вариант от их среднего значения

@4) выборочная дисперсия

Величина, определяемая как квадратный корень из выборочной дисперсии, называется

@2) среднее квадратическое отклонение

Отношение среднего квадратического отклонения к средней величине признака, выраженное в процентах, называется

@3) коэффициент вариации

Разность между наибольшим и наименьшим значениями признака, называется

@4) вариационный размах

Статистическая оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, называется

@1) Несмещенной

Оценка параметра генеральной совокупности, которая определяется одним числом, называется

@2) Точечной

Если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности, такая точечная характеристика называется

@3) Состоятельной

Если точечная оценка генерального параметра имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками, она называется

@4) Эффективной

Если математическое ожидание точечной оценки равно оцениваемому параметру при любом объеме выборки, она называется

@1) Несмещенной

Из следующих оценок параметров генеральной совокупности несмещенной является

@2) выборочная средняя

Числовой интервал, который определяется двумя числами – границами интервала, содержащий неизвестный параметр генеральной совокупности, называется

@2) Интервальной оценкой

Интервал, в котором с той или иной заранее заданной вероятностью находится неизвестный параметр генеральной совокупности, называется

@1) доверительным интервалом

Вероятность того, что исследуемая величина выйдет за назначенный ей интервал, называется

@3) уровнем значимости

Величина, которая характеризует точность выборочного среднего и определяется делением выборочного среднего квадратического отклонения на квадратный корень из объема выборки, называется

@4) ошибкой выборочной средней

Любое высказывание о генеральной совокупности, проверяемое по выборке, называется

@2) статистическая гипотеза

В математической статистике гипотезу обозначают

@1) H

Гипотеза H0, заключающаяся в том, что сравниваемые генеральные параметры равны и различия, наблюдаемые между выборками случайны, называется

@3) основная

Гипотеза H1, противоречащая H0 и заключающаяся в том, что сравниваемые генеральные параметры различаются, называется

@1) альтернативная

Вероятность ошибки отвергнуть нулевую гипотезу, если в действительности она верна, называется

@4) уровень значимости

Уровень значимости выбирается следующим образом:

@1) задается исследователем

Уровень значимости принимается равным

@2) малому числу (0,001; 0,01, 0,05)

Число, которое не может стать уровнем значимости

@4) 0,5

Число, которое может стать уровнем значимости

@2) 0,05

Правило, позволяющее основываясь только на выборке принять или отвергнуть нулевую гипотезу, называется

@3) статистический критерий

Критерий в математической статистике обозначается в общем случае

@4) K

Наблюдаемое значение критерия определяется следующим образом

@4) по формуле

Критическое значение критерия определяется следующим образом

@1) по таблице

Критическое значение критерия зависит от

@3) числа степеней свободы и уровня значимости

Критическое значение критерия не зависит от

@3) математического ожидания

Справедливость нулевой гипотезы проверяется

@2) сравнением наблюдаемого значения критерия и критического

При использовании параметрических критериев нулевая гипотеза принимается при

@1) Кнабл меньше Ккрит

При использовании параметрических критериев в случае, когда Кнабл меньше Ккрит,

@3) принимают нулевую гипотезу

При использовании непараметрических критериев нулевая гипотеза принимается при

@3) Кнабл больше Ккрит

При использовании непараметрических критериев в случае, когда Кнабл больше Ккрит,

@3) принимают нулевую гипотезу

К параметрическим критериям проверки статистических гипотез относится

@2) Критерий Стьюдента

К параметрическим критериям проверки статистических гипотез не относится

@3) Критерий знаков

Параметрический статистический критерий - это функция, зависящая от

@2) параметров данной совокупности

Требование, которое не предъявляется к выборке для применения параметрических критериев проверки статистических гипотез

@4) экспоненциальный закон распределения

Для проверки гипотез о равенстве средних из параметрических критериев используют критерий

@3) Стьюдента

Критерий Стьюдента обозначается следующей буквой

@2) t

К выборке для корректного использования критерия Стьюдента при проверке гипотезы о равенстве средних не предъявляется требование

@4) экспоненциальный закон распределения

Число степеней свободы для определения критического значения критерия Стьюдента в задаче проверки гипотезы о равенстве средних значений в выборках определяется по формуле

@3) f=n1+n2-2

В случае, если при проверке гипотезы о равенстве средних выяснилось, что наблюдаемое значение критерия ниже критического, можно сделать вывод

@2) различие генеральных средних незначимо

Для проверки гипотез о равенстве дисперсий из параметрических критериев используют критерий

@2) Фишера

Критерий Фишера обозначается следующей буквой

@3) F

К выборке для корректного использования критерия Фишера при проверке гипотезы о равенстве дисперсий не предъявляется требование

@4) экспоненциальный закон распределения

Наблюдаемое значение критерия Фишера равно

@1) отношению большей дисперсии к меньшей

Наблюдаемое значение критерия Фишера всегда

@5) больше либо равно единице

В случае, если при проверке гипотезы о равенстве дисперсий выяснилось, что наблюдаемое значение критерия выше критического, можно сделать вывод

@3) различие генеральных дисперсий значимо

Один из критериев, при помощи которого проверяют соответствие закона распределения выборочных данных некоторому известному закону распределения

@3) Пирсона

Критерий, с помощью которого не исследуют соответствие закона распределения выборочных данных некоторому известному закону распределения

@1) Стьюдента

Число степеней свободы для определения критического значения критерия Пирсона в задаче проверки гипотезы о соответствии распределения заданному закону

@4) f=k-3

В случае, если при проверке гипотезы о соответствии закона распределения выбранному известному выяснилось, что наблюдаемое значение критерия меньше критического, можно сделать вывод

@3) данные наблюдений согласуются с выбранным законом распределения