Учебник Каллер

1 .3. ЧАСТОТНОЕ И ВРЕМЕННОЕ ПРЕДСТАВЛЕНИЯ

ОСНОВНЫМИ

НЕПРЕРЫВНЫХ ВОЗДЕЙСТВИЙ И РЕАКЦИЙ

задачами ТЛЭ

Ц

является

н

н

или обеспече­

уста овле ие

этом некоторые напр яжения или токи подводятся к цепи извне и явля­

ются причи ной возникновен ия

электромагнитных процессов в

ней .

Такие

апряжения

или

токи

н

аз

о Д

н

ы

м и

или в о з Д е й­

н

ывают в х

с т в и я м и .

Другие

напряжения

и токи

являются следствием

первых ,

их называют

в ы х о

н ы м и ,

или

р е а к ц и я м и .

В

система

х

тел

меха

н

ики и связи воздействия и реакции представ­

е

П

и

токи, разнообразно и достаточно сложно из­

ляют собой напряжения

меняющиеся

во времен и .

Их

Д

сообщений и на­

используют для передачи

зывают

с и г н а л а м и .

которую п р иходится решать

при анализе

оэтому первой задачей,

и синтезе элек рических

цепей для преобразова

и я и

а

передачи сигн

­

т

н

и я свойст

в

лов

является

ыбор математи ческих

средс

для отобр ажен

.

в

тв

последни х .

Отображение свойств сигналов, как и свойств реаль ны х устройств,

схемами

Ц

с целью

у прощени я

ма ематическо о

аппарата

част

ЛЭ

Т

т

г

о­

ходных сигналов (воздействий и реакций) во всех случаях

сводится

к представлени ю сложного сигнала суммой более просты х . Простыми

сигналами могут быть разные наборы элементар ных сигналов.

ЛЭЦ

в качестве т

аких элемент

арных сиг

налов

преимущественно

ользуют

н

ие.

испВ Т

вле

е'n .

гармонические

колебания,

узкие импульсы и сигналы вида

Частот ое

предста

н

а

вля

­

Если в качестве элементарных сост

рят о частотном представлени и .

р яде случаев реальные сигналы

с известн ой степенью приближениВя

можно считать периодическими .

Периодический

снгнал с помощью р яда Фурье может быть разложен

на сумму гармонически х

(си нусоидальных или косинусоидальных)

составляющих

с

крат ыми

частотами

:

н

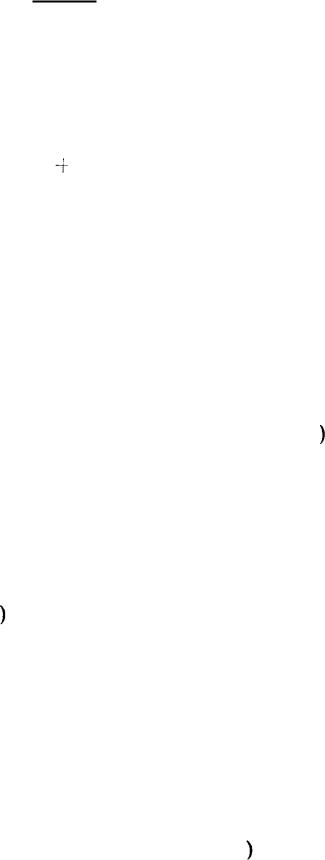
L·изображеиие F (р)

Т а б л и ц а 1.1

ОригнналJ ( f)

(t)

( J/p

6 (t)

2

e'fat

1/(Р

+

а)

(1) /

(0 )

siПооl

р2

rде 'Р= arctg оо/а

1/Ур2+2ар

e-аtJо(jаt)

е-а'Jo (ja Vt2-'Ji)

при t >.0

Jn (at)

, n> 1

)

лов вместо гармонических колебаний,

(2Vt ) = -erf ( 2 1 1'/

изображаемых функциями

воспользоваться сигналами вида

где

р

комплеКсное

число, то

erfc

л

I

л

ei(i)/,

преобразования Фурье переходят eв преобразования Лапласа:

00

Pt,

-

-J0 0 f (/) е

Р' d/=р (р) =LIf (1 )1;

c+ioo

Р'

.....S F!-)

dp=f (1)=L-IIF (p)l.

21tj

(р

е

Преобразования Фурье и Лапласа широко применяют в

ЛЭЦ

перехода от функций

времени

(t) ,

(t)

к

их

или

изображе­

ниям

iJ(00),

i

(00)

илиc-ioo(р),

(ри). При этом , как известноF-

, используют

iJ

таблицы преобразований. Некоторые L-преобразо

ания,

котор

потребуются в дальнейшем, 1приведенiы в

табл . ·

в

ые

ВременнОе

представление.

При использовании в

качестве элемен­

J.J.

Напряжение

конечного во

времени

произвольно измен яющегося непрерыв­

ного сигнала можно представить после­

t

довател ьностью действующи х один за

другим импул ьсов (рис . 1 . 9) и выразить

Рис.

1 .9

формулой(t).

= JОt

и

('t) li (t -'t) d't.

т

(1

. 1 4)

и

называют и '{;

р а­

Здес ь

единичный импульс,

и ('t)d't­

.Jl о м Н а л о ж е н и я ,

или с в е р т к о й .

'{,

6 (t-'t)-

действующий в момент

как бы значение и мпульса напряжения, действующего в момент

а

и (t) представляет собой сумму импульсов, поступающих в последова­

тельные моменты времен и .

Выражение ( 1 . 1 4)

н

е г

Il* (/)

k

k

=u (t) li(t

-kТ) = (kT) б (t -kТ).

(1 . 15)

Выражение ( 1 . 1 5)

я вляется

дискретным аналогом интеграла нало­

11

жения (1. 1 4) . Спектр напр яжения такой последовательности и мпульсов

(

=

00о k

k

k

T)

eifJJkT

.

(1 . 16)

F u*(t)J

S u (kT) б (t -kr) e-j(l)t dt

=

u(

исходного непрерывного сигнала (; (ro) выражением

F[Il*(t)J=Iu(n )e--ifJJnТ=U*(оо)=

m=+оо

U(oo-2тооJ).

I

(1 .17)

где

n

T

m=

--00

По аналогии с периодически­

ми

непрерывными

сигналами

Рис. 1 1 1

рассмотрим

также

периодиче­

ские импульсные

(дискретные)

сигналы.

дическую после

­

Перио

Рис.

1.10

довательность импульсов можно

.

представить рядом Фурье в виде

с

частотами,

кратными

ос­

суммы

гармонических

составляющих

новной

частоте периодической последовательности 0)0

= 2n/(NT),

где

N

- число импульсов в одном периоде последовательности, Т-

ин­

тервал между импульсами

(рис. 1 .1 1).Из выражения (1 . 16) видно,

что

разложение

периодической импульсной

последовательности

в

ряд

Фурье содержит всего

N различных частотных составляющих с

пери­

одом, равным целой части периода колебаний основной частотой

0)0'

поскольку функция и (t) не равна нулю только в дискретные моменты

времени

kT

и, следовател

ьно,

еjkЮ•Т

=

ejk (21t/N)

периодически

пов­

N частот определяет

торяется, если k > N.

Таким образом,

множество

все различные частоты, кратные основной частоте

0) '

0

Коэффициенты разложения периодической импульсной последова­

тельности в ряд Фурье,

представляющие собой дискретные составляю­

щие спектра.

N-1

-j

2лkn

И

N

( 1 . 18)

(пы,,) =

u (kT) е

k=O

Выражения (1

. 18) и (1 . 19) являются парой преобразований,

пред­

ставляющих периодическую последовательность дискретным рядом

Фурье (ДРФ). Если рассматривать только один период периодической

импульсной последовательности,

считая его просто импульсной после­

довательностью конечной длины,

и соответственно один период после­

довательности КОэффициентов в частотной области, то переходим к паре

преобразований:

{N_I

] '

U (n()),,) = k O U(kt)eXP [ -i

N

21tkn

_

(1

.20)

О <П<N-J. }

(1

.21 )

u (1)

L [и (1)]

z[u· (/)]

Т а б л и ц а 1.2

1

(I)

р

z

г-1

e-al

z

1 -е -al

г_е-ат

р

(г-1) (г_е-ат)

siп (j)t

zsiпwТ

г2 -2г cos ыТ + 1

z (z-cos ыТ)

coswt

г2 -2г cos ыТ + I

Выражения (1 .20) и (1 .21)

называют соответственно прямым и об­

ратным

д и с к р е т н ы м и

п р е о б р а з о в а н и

я м и Фурье

(ДПФ) .

Эти выражеlfИЯ весьма удобны для вычисления на ЭВМ, чем

(1 . 1 5), то при определении ее реакции на них в момент kT операторным

методом

вместо преобразоваНI"Я Лапласа

(;*

(р)

=

L lu*] удобнее

применять специальные преобразования функций

в

и

(z), назы­

ваемые

z-преобразованиями.

и* (t)

Суть

z-преобразования заключается в замене e-рkТ в выражении

(; (р) =

L [и* (t)] = (k)и (kT)e-рkТ на z и введении

(1 .22)

и (г) = 1:u (kT) z-k.

k

таблицам L- и F-преобразованиЙ.

L [и (/)1 = IIр,

Пусть, например, u (t)

= 1

(t).

и· (t) =

1:

1\

(t-

kT);

L

(u* (t)] =};е -рkТ;

L-преобразованию I/p соответствует

z-преобразование г/(г - 1) и

L [u(t»)==

1

;

u*

,.,

{j

р+а

(t)="z.e--

L [u* (/»)

V

)

аkТ

(t-kТ);

e

аkТ

e-аkТ z-k=z/(z -е -ат);

=

-

е -рkТ;

(z

=

k

а)

k

L-преобразованию

li(p

соответствует z-преобразование

z/(z - е-ат). Аналогично

можно

получить

и другие соответствия.

+

Некоторые

из

них

сведены

в

табл. 1 .2.

табл.

1 .2 приведены наиболее часто встречающиеся и используе­

мыеВ далее

преобразования.

1.5. ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕй

Свойства цепи определяются

ее

реакцией на те или иные воздейст­

весия напряжений для цепи (см.

рис 1 . 12) имеет вид:

ri+L -di. + -Сl

S idt=u(t).

(1

. 23)

dt

Z (00)= r+jooL +

--.

=r+jx -

(1.25)

JooCl

у (00) = I/Z (00),

х а р а к т е р и с т и к а­

z (ю) и У (ю) называют ч а с т о т н ы м и

м и

цепи.

Комплекс полной проводимости можно представить в вире

у

(00)

=g(00)-+ jb (00)

,

(1.26)

где g (oo) =г/ I Z (00) I 2 - активная проводимость цепи ;

Ь

(00)= -х/ I Z (00)

I 2 - реактивная проводимость

цепи.