
Крючков В.П. Физика реакторов для персонала АЭС с ВВЭР и РБМК
.pdf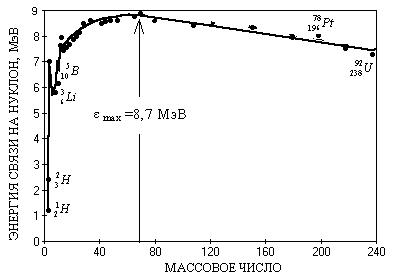
Каждый нуклид обозначается химическим символом (X ) с указанием атомного номера Z
и массового числа А ZA X (эквивалентное обозначение АХZ), например 1Н1, 10В5, 238U92 или кратко AХ, например, 1Н, 10В, 238U.
1.6. Энергия связи ядер
Масса (М) любого ядра меньше суммы масс свободных изолированных нуклидов
Zmp Nmn M . |
(1.6.1) |
||
Разность масс соответствует энергии связи Eсв , которая бы выделилась при образовании |
|||
ядра из изолированных нуклидов. Энергия связи: |
M)c2 . |
|
|
Eсв (Zm |
Nm |
(1.6.2) |
|
|
p |
n |
|
Из сказанного понятно, что энергию связи можно также определить как энергию, которую необходимо затратить для полного разделения ядра на нуклоны. Энергия связи является следствием сил притяжения нуклонов, т. е. имеет природу ядерного взаимодействия.
Ядерные силы, связывающие нуклоны в ядре, компенсируют силы кулоновского отталкивания протонов, делая ядро устойчивым. Ядро тем стабильнее, чем больше энергия связи, приходящаяся на один нуклон ( ):
Eсв / A.
(1.6.3)
Как видно из рис. 1.1, средняя энергия связи для большинства ядер находится в диапазоне 8 – 9 МэВ, хотя для легких ядер (А<20) она изменяется от 1МэВ для 2Н1 до 8 МэВ.
Рис.1.1. Зависимость средней энергии связи на один нуклон от массового числа А ядра
Средняя энергия связи нуклонов в ядре намного больше средней энергии связи атомов в молекуле: так, при делении ядра урана выделяется энергия, равная 200 МэВ, тогда как при прохождении химической реакции, связанной, например, со взрывом тринитротолуола, выделяется менее 10 эВ на молекулу.
1.7. Получение ядерной энергии
Поскольку система нуклонов стремится перейти в наиболее устойчивое состояние (такое состояние соответствует максимально возможной значению энергии связи), то
11
любая эволюция ядра происходит с увеличением энергии связи. Суммарная масса системы при этом уменьшается, следовательно, учитывая связь массы с энергией, высвобождается энергия. Как видно на рис.1.1, возможны два типа ядерных реакций с выделением энергии:
реакция деления – процесс деления тяжелых ядер, например, урана или плутония на более легкие с испусканием нейтронов. Реакция деления является ядерно-физической основой для ядерных реакторов (детально реакция деления будет рассмотрена ниже); реакция синтеза – процесс образования одного тяжелого ядра из двух легких. Реакция
синтеза происходит в результате столкновения ядер. Необходимое условие протекания реакции синтеза – кинетическая энергия сталкивающихся ядер должна быть больше кулоновского барьера ядер. Такая энергия может быть достигнута при нагреве плазмы, состоящей из легких ядер (ядер, имеющих малую удельную энергию связи), до температуры ~ 108 К.
1.8. Основные виды радиоактивного распада ядер
Альфа-распад
В процессе α-распада материнским ядром (ZA X ) испускается α-частица (ядро гелия 24He):
ZA X 24He ZA 24X
Альфа-распад наблюдается только у тяжелых ядер (Z > 82). Если дочернее ядро X образуется в возбужденном состоянии, то после испускания α-частицы испускается γ- квант.
Бета-распад
В процессе β-распада ядро испускает электрон и антинейтрино или позитрон и
нейтрино. |
ZA X Z A1X e ~e ; |
β--распад – |
|
β+-распад – |
ZA X Z 1AX e e . |
Вслучае, если образующееся в результате β-распада ядро X перегружено нейтронами имеет при этом энергию возбуждения, превышающую энергию связи, то одним из каналов снятия возбуждения ядром является испускание нейтрона. Испускание нейтрона происходит с запозданием относительно момента β-распада. Время запаздывания определяется временем жизни возбужденного дочернего ядра X . Запаздывающие нейтроны имеют принципиальное значение в работе ядерного реактора, (К обсуждению их характеристик и их роли в управлении реактором мы будем ниже неоднократно возвращаться).
Спонтанное деление
Вслучае спонтанного деления тяжелое ядро самопроизвольно распадается на несколько частей (чаще всего на две) с одновременным испусканием быстрых нейтронов. Именно процессом спонтанного деления ограничивается стабильность тяжелых атомов и искусственного получения сверхтяжелых ядер (с Z > 120).
1.9.Закон радиоактивного распада ядер
Радиоактивность – есть свойство определенных нуклидов спонтанно испускать частицы или γ-кванты.
Среднее изменение числа радионуклидов описывается законом радиоактивного распада
N(t) N0e t |
(1.9.1) |
12

где N0 – число радионуклидов в образце в момент времени t = 0; N – число
радионуклидов в образце в момент времени t; λ – постоянная распада, c-1; t – время ,c. Приведенный закон справедлив для любого типа распада (α-, β-распад,
спонтанное деление). Широко используемая в ядерной и реакторной физике такая характеристика радиоактивного распада, как период полураспада Т½,, связана с постоянной распада соотношением
Т½ =0,693/ λ.
Если в начальный момент времени t = 0 имелся только материнский радионуклид, характеризуемый числом радиоактивных ядер N10, то для цепочки радиоактивного распада из двух последовательно распадающихся нуклидов с постоянными распада λ1 и λ2 изменение числа ядер в зависимости от времени записывается как
N2 |
(t) |
N10 2 |
(e 1t e 2t ) |
|
(1.9.2) |
|||
|
|
|||||||
|
2 |
1 |
|
|
|
|
||
По истечении большого времени (t ~ 0,693( |
) ) наступает равновесие: |
|||||||
|
|
|
|
2 |
1 |
|
||
N2 |
(t) |
N1(t) 2 |
. |
|
(1.9.3) |
|||
|
|
|||||||
|
2 |
1 |
|
|
|
|||
В случае, если период полураспада материнского ядра на много больше периода |
||||||||
дочернего ядра (T1 |
)1 (T1 |
)2 (или, что то же самое, |
1 2 ), и по истечении времени, |
|||||
2 |
2 |
|
|
|
|
|
||
достаточно большого по сравнению с периодом полураспада материнского ядра (T1 )1 , |
||||||||
|
|
|
|
|
|
|
|
2 |
наступает “идеальное равновесие” (или “вековое равновесие”):N1(t) N2 (t) |
||||||||
1.10. Действие ядерных сил в ядре
Ядро удерживается в стабильном состоянии благодаря действию ядерных сил притяжения между нуклонами. Ядерные силы в ядре обладают следующими свойствами: короткодействие – расстояние на котором они проявляются, менее ~ 10-13 см;
ядерные силы являются силами притяжения и сильнее, чем электростатические силы
отталкивания внутри ядра;
ядерные силы не зависят от электрического заряда, т.е. они действуют одинаково на пары протон – протон или протон-нейтрон;
ядерные силы обладают свойством насыщения, т.е. нуклон может взаимодействовать только с несколькими ближайшими нуклонами.
1.11. Устойчивые и неустойчивые ядра
Устойчивость ядер зависит от соотношения в нем чисел нейтронов и протонов, т.е. от параметра (A Z)/Z . Наиболее устойчивы ядра легких нуклидов при
(A Z)/Z = 1, т.е. при равенстве чисел протонов и нейтронов (рис. 1.2). Тяжелые ядра, как видно из рис.1.2, более устойчивые в случае некоторого преобладания числа нейтронов над числом протонов, что обусловлено компенсацией электростатических сил отталкивания между протонами и силами ядерного взаимодействия между нуклонами (нейтронами и протонами). На этом же рисунке показаны области соотношений нейтронов и протонов с типичными распадами.
13
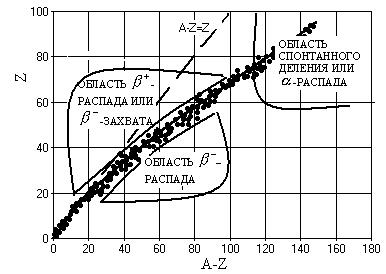
В случае преобладания нейтронов ядра переходят в более устойчивое состояние путем β--распада, в случае избытка протонов идет β+-распад.
Рис.1.2. Зависимость числа протонов в ядре (A-Z) от числа нейтронов для стабильных ядер
Ядра с большим числом нуклонов неустойчивы по отношению как к α-распаду, так и к спонтанному делению.
Наиболее устойчивые ядра те, которые имеют четное число нейтронов и протонов (четно-четные ядра), менее устойчивые – четно-нечетные и самые нестабильные – нечетно-нечетные. Это свойство ядер объясняется способностью нейтронов и протонов с противоположно направленными спинами (антипараллельными) группироваться в ядре парами.
Самыми устойчивыми являются ядра, в которых число нейтронов и протонов, соответствует “магическим числам”: 2, 8, 20, 50, 82, 126, 184. Примером такого ядра служит ядро 20882 Pb, имеющее четное число как нейтронов, так и протонов (четно-четное ядро), и потому наиболее стабильное.
1.12.Капельная модель ядра
Наиболее простой и одновременно продуктивной моделью, позволившей объяснить основные свойства ядра, является капельная модель. В основу модели положена аналогия между ядром и каплей жидкости. Основные положения модели: 1) ядерная жидкость несжимаема; 2) ядро имеет форму шара; 3) плотность электрического заряда в ядре постоянна; 4) сила притяжения между нуклонами не зависит от их электрического заряда.
Модель позволяет с хорошей точностью описать зависимость энергии связи Eсв от A и Z нуклида. Эта зависимость, называемая формулой Вайцзеккера, представляется как
Eсв A A |
2/3 |
|
Z2 |
|
(A/2 Z)2 |
A |
3/ 4 |
, |
(1.12.1) |
|
|
A1/3 |
A |
|
|
||||||
|
|
|
|
|
|
|
|
|
||
где =15,56 МэВ; |
=17,23 |
МэВ; =0,7 |
МэВ; =34 МэВ; |
1 (для четно-четных |
||||||
ядер), 0 (для четно-нечетных ядер), -1 (для нечетно-нечетных ядер).
Первый член этой формулы (1.12.1) отражает факт взаимодействия нуклонов в ядре только с ближайшими нуклонами, подобно молекулам капли жидкости. Второй член корректирует энергию связи на наличие “поверхностных” нуклонов, слабее связанных с соседними нуклонами, подобно молекулам на поверхности капли. Третий член учитывает кулоновское отталкивание между протонами ядра. Четвертый член не имеет аналогии в классической теории капли и обусловлен неодинаковым числом нейтронов и протонов в
14
ядре. Пятый член передает экспериментально установленный факт зависимости энергии связи от четности числа протонов и нейтронов в ядре.
1.13. Другие модели ядра
Из других моделей наибольшее распространение и развитие получила оболочечная модель, основанная на квантово-механическом описании состояний нуклонов в ядре. Согласно оболочечной модели энергетическая структура ядра определяется коллективными энергетическими уровнями, соответствующими совокупности квантовых чисел. Модель объясняет причину особой устойчивости ядер в основном состоянии, с числом нуклонов, равным одному из магических чисел. Нуклоны в ядрах расположены в оболочках с ограниченным числом состояний. Те из них, которые находятся в незаполненных оболочках, менее связаны, подобно валентным электронам в атоме, и уменьшают устойчивость ядра. Ядро с полностью заполненными оболочками, напротив, оказывается наиболее устойчивым. Оболочки заполнены, когда число находящихся на них нуклонов равно одному из магических чисел.
Основные положения оболочечной и капельной моделей не противоречат одна другой (модели предназначены для описания разных характеристик ядра) и поэтому могут быть объединены в рамках единой обобщенной модели. Такие модели, опирающиеся на информацию об энергетической структуре ядра, феноменологическом представлении о нуклон-нуклонных взаимодействиях, ядерном потенциале, позволяют воспроизводить основные свойства и характеристики ядра и ядерных реакций.
Вопросы к разделу Основы ядерной физики
1.Какими фундаментальными взаимодействиями определяются ядерные процессы в реакторе?
2.Какие субатомные частицы участвуют в физических процессах в активной зоне реактора? Назовите основные характеристики этих частиц.
3.Какие основные постулаты модели Бора?
4.Что такое нуклиды, радионуклиды, изотопы?
5.Что такое энергия связи ядер? Какие типы ядерных реакций могут использоваться для получения энергии?
6.Какие виды радиоактивного распада реализуются в реакторе?
7.Сформулируйте закон радиоактивного распада.
8.Назовите основы капельной модели ядра.
2. Необходимые сведения из нейтронной физики
2.1. Нейтроны
Нейтрон – субатомная частица, благодаря ядерным взаимодействиям которой возможно производство энергии в реакторах деления.
Основные свойства нейтрона – масса 939,57 МэВ, электрический заряд 0. Нейтрон относится к фермионам, т.е., имея спин ½, подчиняется статистике Ферми. Квантовые числа нейтрона подчиняются принципу Паули, исключающий нахождение в каждом квантово-механическом состоянии более одной частицы. Диапазон кинетической энергии нейтронов в ядерном реакторе простирается от ~ 10-3 до ~ 107 эВ. Как следует из основ квантовой механики, длина волны нейтрона (де Бройлевская длина волны ) связана с его импульсом ( p ) (или кинетической энергией (E ) соотношением
/ p 4,45 10 10 |
|
, |
(2.1.1) |
|
|||
|
E |
|
|
15
где h/2 ; h – постоянная Планка.
Из (2.1.1) следует, что волновые свойства нейтрона проявляются в основном при малой энергии. Длина волны нейтрона энергией ~ 10-3 эВ имеет порядок размера атомов и молекул (~ 10-7 см). При большой энергии нейтронов их можно рассматривать как точечные частицы, взаимодействующие с ядрами и внутриядерными нуклонами.
При рассмотрении взаимодействия нейтронов с ядрами принято указанный энергетический диапазон делить на три интервала – область тепловых 10-3 – 0,625 эВ, промежуточных (или резонансных) 0,625 эВ – 1 кэВ и быстрых нейтронов 1 кэВ – 10 МэВ, а нейтроны, которые имеют энергию, соответствующую указанным диапазонам – называются тепловыми, промежуточными и быстрыми.
2.2. Плотность потока (поток) частиц
Приведенные в этом разделе определения относятся, в общем случае, к любым частицам, хотя речь будет идти, в основном, о нейтронах.
Ключевой характеристикой поля нейтронов в реакторе, входящей в определение большинства нейтронно-физических параметров реактора, является поток нейтронов. (Поток нейтронов – принятый в физике реакторов жаргон, которым мы также будем пользоваться. Правильный термин – плотность потока нейтронов).
Поток нейтронов (плотность потока) (r,t) в некоторой точке пространства (r )
есть число нейтронов, которые пересекают поверхность элементарной сферы с центром в данной точке в секунду, отнесенное к площади центрального сечения этой сферы. Несложно понять, что если плотность нейтронов (число нейтронов в единице объема) n, а их скорость , то плотность потока:
(r,t) n(r,t) . |
(2.2.1) |
Выражение (2.2.1) написано для нейтронов, имеющих одинаковую энергию. На практике нейтроны почти всегда обладают непрерывным распределением по энергии в
интервале Е1 – Е2. В этом случае плотность потока нейтронов с энергией |
в пределах от Е |
до Е + dЕ (соответственно скоростей от до d ) составит |
|
(r,E,t)dE n(r,E,t) dE . |
(2.2.2) |
Здесь величина n(r,E,t) характеризует энергетическое распределение плотности
нейтронов (спектральная плотность), |
(r,E,t) – |
энергетическое распределение потока |
||||
(спектральный поток, или спектр) |
нейтронов в |
точке r |
и в момент времени t. |
|||
Интегральный в указанном диапазоне энергии поток нейтронов тогда будет равен |
||||||
|
E2 |
|
E2 |
|
|
(2.2.3) |
(r,t) (r,E,t)dE n(r,E,t) (E)dE . |
||||||
|
E1 |
|
E1 |
|
|
|
Плотность тока нейтронов |
j – вектор, |
равный по модулю плотности потока |
||||
нейтронов и имеющий направление, которое совпадает с направлением распространения нейтронов :
j . |
(2.2.4) |
Ток нейтронов в направлении r |
(правильней проекция тока на r ) есть модуль |
вектора, который равен разности числа нейтронов, пересекающих площадку единичной площади, расположенную перпендикулярно r в противоположных направлениях, в единицу времени. Размерность тока и плотности тока с-1· см-2.
Приведем еще одно понятие, часто используемое при решении многих практических задач реакторной физики, таких, например, как воздействие нейтронов на реакторные материалы, определение ресурса корпуса реактора и внутрикорпусных устройств. Это понятие “флюенс нейтронов” (r) – отношение числа нейтронов, которые пересекают поверхность элементарной сферы с центром в точке r за некоторое время,
16
отнесенное к площади центрального сечения этой сферы. Флюенс нейтронов за время Δt равен потоку нейтронов, проинтегрированному по интервалу времени от t до t + Δt:
|
t t |
|
|
(r) |
(r,t)dt . |
(2.2.5) |
|
t
2.3. Эффективное сечение взаимодействия
Под взаимодействием частиц с веществом в реакторной физике понимают их столкновения с ядрами вещества. Вероятность реакции частицы с ядром (будем рассматривать, в основном, только нейтрон-ядерные взаимодействия) называется
микроскопическим сечением (или эффективным сечением, или просто сечением) данной реакции.
Эффективное сечение может быть определено следующим образом. Пусть - число нейтронов, которые падают на тонкую пластину, перпендикулярную ее поверхности (плотность потока нейтронов, с-1· см-2). Число атомов в единице объема пластины (плотность атомов) N . При прохождении нейтронов с плотностью потока R из них провзаимодействует с атомами. Тогда сечение взаимодействия есть отношение
R/(N ). |
(2.3.1) |
Величина R называется скоростью реакции и представляет собой число взаимодействий нейтронов в единичном объеме за 1 с.
Сечение имеет размерность квадрата длины и измеряется в см2 или в барнах: 1барн = 10-24 см2. Сечение определяется вероятностью взаимодействия нейтрона с ядром. Микроскопическое сечение имеет простую геометрическую трактовку – это площадь поперечного сечения некоторой пространственной области взаимодействия нейтрона с ядром. Микроскопическое сечение пропорционально (но в общем случае не равно) площади сечения ядра и нейтрона. В области больших энергий (E 1 МэВ) сечение приближается к значению, равному площади поперечного сечения ядра.
Сечения зависят от сорта ядра и энергии налетающего нейтрона. В зависимости от типа взаимодействия сечения обозначаются так: σa (absorption) – сечение поглощения, σc (cepture) – сечение радиационного захвата (n,γ), σel (elastic) – сечение упругого рассеяния (n,n), σin (inelastic) – сечения неупругого рассеяния (n,n ), σs (scattering) – сечение рассеяния, σf (fission) – сечения деления (n,f), σt (total) – полное сечение. Сечение рассеяния
есть сумма сечений упругого и неупругого рассеяний: |
|
s el in |
(2.3.2) |
Сечение поглощения включает в себя сечения всех процессов, приводящих к поглощению нейтрона. Фактически это захват с делением и радиационный захват:
a |
f |
c . |
(2.3.3) |
Полное сечение есть сумма сечений всех процессов
t |
a s . |
(2.3.4) |
2.4. Макроскопическое сечение
Число взаимодействий нейтрона в определенном объеме вещества зависит не только от микроскопического сечения индивидуального ядра, но и от числа ядер в данном
17

объеме. Чтобы посчитать это число взаимодействий, вводят понятие макроскопического сечения, которое определяется как
|
N , |
(2.4.1 ) |
||
где – макроскопическое сечение см-1 |
; N – число ядер в единице объема |
|
||
N |
NA |
. |
(2.4.2 ) |
|
|
||||
|
|
M |
|
|
Здесь ρ - плотность вещества, г/см3; NA = 6,02209·1023 моль-1 – число Авогадро, M – атомная масса вещества. Для гомогенной смеси ядер K сортов макроскопическое сечение определяется как сумма
K |
K |
xi i |
|
|
|
i |
см NA |
, |
(2.4.3) |
||
|
|||||
i |
i |
Mi |
|
||
где см – плотность вещества смеси г/см3; xi – массовая концентрация i-го элемента; Mi –
атомная масса i-го элемента. В случае химического соединения концентрация рассчитывается как xi ki Mi / Mмол , где ki - число атомов i-го элемента в молекуле, Mмол
– молекулярная масса данного химического соединения.
2.5.Длина пробега и длина диффузии
Пусть плотность потока нейтронов ( (x)), которые падают вдоль оси x на слой вещества толщиной dx, расположенный в точке x 0, равна Ф(0). В результате взаимодействия нейтронов с ядрами в объеме, ограниченном интервалом dx, плотность потока нейтронов уменьшится на величину d (x), пропорциональную плотности потока
(x) |
и макроскопическому сечению взаимодействий : |
|
||
|
d (x) (x). |
( 2.5.1) |
||
Интегрируя уравнения (2.5.1) в пределах от 0 до x , получаем |
|
|||
|
(x) (0)e x |
(2.5.2) |
||
Отсюда следует, что вероятность нейтрону преодолеть расстояние x равно e x . |
Теперь, |
|||
определив средний пробег нейтрона до взаимодействия ( ) как |
|
|||
|
|
|
|
|
|
|
х (х)dх |
(2.5.3) |
|
|
|
|
||
|
|
|||
|
|
|
||
(х)dх
и подставляя формулу (2.5.2) в (2.5.3), легко получить: 1 .
Если под понимать полное макроскопическое сечение взаимодействия ( t ), то
полный пробег записывается как: t 1 . Аналогично записывается длина пробега до
t
18
рассеяния |
|
|
1 |
и поглощения |
|
|
1 |
. Учитывая, что |
|
|
|
|
|
|
, |
то |
||||
|
|
|
s |
|
|
s |
a |
|
|
a |
|
t |
|
s |
|
a |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
1 |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t |
|
s |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В физике ядерных реакторов |
также |
широко используется |
понятие величины |
|||||||||||||||
транспортной длины пробега нейтронов, физический смысл которой есть длина пробега нейтрона в направлении его движения до первого соударения с ядром среды, усредненная
по бесконечному числу рассеяний. |
|
|
|
|
||||||||||||||
|
|
|
В |
s |
отсутствие |
поглощения транспортная длина |
пробега выражается |
как |
||||||||||
|
|
|
|
|
|
|
, где |
|
- |
средний косинус угла рассеяния. Транспортной длине |
|
|||||||
|
|
|
|
|
Cos |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
tr |
1 Cos |
|
|
|
|
|
|
tr |
||||||||||
можно |
|
|
поставить |
в |
соответствие транспортное |
макроскопическое сечение |
||||||||||||
tr |
|
1 |
|
s 1 |
|
. С учетом поглощения tr a s 1 |
|
. |
|
|||||||||
|
Cos |
Cos |
|
|||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
tr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Транспортная длина рассеяния tr значительно отличается от пробега до рассеяния лишь для легких ядер, упругое рассеяние которых анизотропно, например, на водородеtr 3 s . В случае изотропного рассеяния, что имеет место в случае рассеяния на
тяжелых ядрах, Cos 0, следовательно, tr s .
К основным диффузионным характеристикам среды относится длина диффузии (L). Квадрат длины диффузии(L2 ) определяется как шестая часть среднего квадрата расстояния по прямой, на которое смещается нейтрон от точки, где он стал тепловым,
до места его поглощения r2 :
L2 |
r2 /6. |
|
|
|
|
|
|
|
|
(2.5.4) |
||
Квадрат длины диффузии выражается через основные характеристики среды ( tr |
и a ) |
|||||||||||
как |
|
tr a |
|
|
|
1 |
|
|
|
|
|
|
L2 |
|
|
|
|
|
. |
|
(2.5.5) |
||||
|
|
|
|
|||||||||
|
3 |
|
|
|
3 tr a |
|
|
|||||
Вводя понятие коэффициента диффузии, |
|
|
tr |
|
|
|||||||
|
|
D= 1 |
3 tr |
|
, |
(2.5.6) |
||||||
|
|
|
|
|
|
3 |
|
|
||||
получим общепринятое выражение для длины диффузии |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
L |
|
|
D |
|
|
. |
|
(2.5.7) |
||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.6. Взаимодействие нейтронов с ядрами
Из всего многообразия взаимодействий нейтронов с ядрами рассмотрим лишь ядерные реакции, важные для работы ядерных реакторов: рассеяние, поглощение, деление.
Под «рассеянием» понимают ядерную реакцию, при которой после столкновения нейтрона с ядром в конечном состоянии в числе других продуктов реакции остается нейтрон и ядро. Существует два типа рассеяния: упругое и неупругое. При упругом рассеянии нейтроном не передается энергия на возбуждение ядра. В системе нейтрон – ядро сохраняется кинетическая энергия и импульс, т.е. ядро–мишень приобретает то значение кинетической энергии, которое теряет в соударении нейтрон.
Упругое рассеяние может реализоваться двумя способами. В одном из них нейтрон с энергией, близкой энергии резонанса, захватывается ядром, при этом образуется составное (компаунд) ядро. Затем ядро испускает нейтрон таким образом, что полная кинетическая энергия системы нейрон – ядро сохраняется, а ядро возвращается в основное
19

состояние. Это резонансное упругое рассеяние. Энергетическая зависимость сечения резонансного рассеяния имеет характер r ~1/
 E .
E .
Другой способ, называемый потенциальным упругим рассеянием, представляет собой классическое рассеяния двух абсолютно упругих шаров. Сечение потенциального рассеяния p практически не зависит от энергии и в первом приближении определяется
выражением
p 4 R2 , |
(2.6.1) |
где R – радиус ядра.
Упругое рассеяние нейтронов имеет огромное значение в физике ядерных реакторов, поскольку является основным процессом, приводящим к замедлению нейтронов. Кинематика упругого рассеяния описывается формулами классической
механики. Исходя из нерелятивистских соотношений (скорость нейтрона c) |
– закона |
||||||
сохранения энергии и импульса, записанных в лабораторной системе координат |
|
||||||
mn mn Amn яд ; |
|
(2.6.2) |
|||||
|
mn 2 |
|
mn 2 |
|
Amn яд2 |
, |
(2.6.3) |
2 |
|
|
|||||
2 |
2 |
|
|
||||
легко получить связь между скоростью (энергией) нейтрона после рассеяния со скоростью (энергией) до рассеяния:
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E |
1 |
cos |
cos2 A2 1 |
|
|||||||
|
|
|
|
|
|
|
(2.6.4) |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
E |
A 1 |
|
|
|
|||||
Здесь ,E , |
|
|
|
E |
|
– скорость и энергия нейтрона до и после рассеяния; |
яд -скорость, |
||||||||
, |
|
||||||||||||||
приобретенная ядром после рассеяния; – угол рассеяния нейтрона; А – массовое число ядра. В приведенных кинематических соотношениях использованы два приближения: 1) ядро до взаимодействия с нейтроном покоится (учет теплового движения и химических связей является отдельной сложной задачей); 2) масса ядра полагается равной сумме масс внутриядерных нуклонов (здесь разницей между массами нейтронов и протонов пренебрегается, т.е. M яд Amn .)
Из соотношения (2.6.4) следует, что максимальное уменьшение энергии нейтрона для всех ядер-мишеней, кроме водорода, происходит в случае лобового удара ( ):
(2.6.5)
|
Eмин' |
cos2 , |
предельный угол рассеяния нейтрона равен |
|
. При рассеянии на угол |
|
E |
||||
|
|
|
2 |
|
|
|
нейтрон останавливается, передавая ядру водорода всю энергию. Таким образом, |
||||
2 |
|
|
|
|
|
водород является самым эффективным замедлителем нейтронов.
Неупругое рассеяние. В случае неупругого рассеяния налетающий нейтрон поглощается ядром, образуя компаунд-ядро в возбужденном состоянии. Далее компаунд-ядро испускает нейтрон, передавая ему значительную часть энергии возбуждения. Остаточное возбуждение ядро снимает испусканием одного или двух -квантов, переходя в основное состояние.
В неупругом рассеянии сумма кинетических энергий испускаемого нейтрона, ядра-мишени и полная энергия испускаемых γ-квантов равна кинетической энергии налетающего нейтрона. Энергетическая зависимость сечения неупругого рассеяния носит
20
