АОПИ. Лекции / 10

§. Разрешимость алгоритма. Описание алгоритма с помощью машины Тьюринга.

Не для любой задачи можно построить алгоритм. В самом начале курса указано, что одним из свойств алгоритма является массовость, то есть его применимость к определенному множеству входных данных, то есть по сути к определенному классу задач. Вместе с тем есть такие классы задач, для решения которых нет и не может быть единого универсального метода. Такие задачи называются алгоритмически неразрешимыми задачами.

Отметим, что алгоритмическая неразрешимость класса задач не означает невозможность решения конкретной задачи данного класса. Проблема заключается в невозможности решения всех задач данного класса одним и тем же способом.

Пример.

Совершенные числа - это числа, которые равны сумме своих делителей, например: 28 = 1+2+4+7+14.

Определим функцию S(n) = n-ое по счёту совершенное число и поставим задачу вычисления S(n) по произвольно заданному n. Нет общего метода вычисления совершенных чисел, мы даже не знаем, конечно ли множество совершенных чисел, поэтому наш алгоритм должен перебирать все числа подряд, проверяя их на совершенность.

Алгоритмическую неразрешимость задачи можно понимать следующим образом: для любого алгоритма, решающего данную задачу, существует набор входных данных x, на котором алгоритм работает неверно (либо возвращает неправильный результат, либо вообще зацикливается).

Примечание. Даже при наличии алгоритма он может быть неприемлем по своей ресурсоемкости (см. предыдущий параграф).

К сожалению, даже при алгоритмически разрешимой задаче, то есть существовании алгоритма, обладающего необходимой массовостью, невозможно определить сложность самой задачи как сложность наиболее эффективного алгоритма, решающего эту задачу (определенной размерности n). Невозможность вытекает из теоремы Блюма об ускорении, согласно которой есть задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм, решающий эту задачу. Сама теорема Блюма формулируется следующим образом:

Теорема Блюма об ускорении

Существует такая алгоритмически разрешимая задача Z, что любой алгоритм A, решающий задачу Z, можно ускорить следующим образом: существует другой алгоритм A′, также решающий Z и такой, что TA’(n) ≤ log(TA(n)) для почти всех n.

Примечание. Из теоремы Блюма не следует, что ускорение возможно для любой задачи. Вместе с тем утверждение теоремы Блюма о существовании «неудобных» задач не позволяет определить универсальное (применимое ко всем задачам) понятие «оптимального алгоритма».

В теории сложности принято относить алгоритм к одной из моделей машины Тьюринга. Каждая модель машины Тьюринга представляет собой определенный способ формального описания алгоритма. Машина Тьюринга отличается от реальной машины бесконечной памятью.

Машина Тьюринга (МТ) имеет три составных компонента:

1.Память в виде бесконечной в обе стороны ленты, разделенной на ячейки, в каждую из которых

может быть записана либо одна из букв внешнего алфавита {a1, a2, ..., ak}, либо пустой символ, который обозначается греческой буквой Λ и добавляется к алфавиту в качестве символа a0. Внешний алфавит A = {a0, a1, a2, ..., ak} может быть отличным для каждой МТ, но всегда является конечным. На любом шаге работы МТ только конечный участок ленты может содержать буквы внешнего алфавита, а в каждой ячейке может находиться только один символ из алфавита.

2.Автомат, состоящий из устройства управления и считывающей головки, который на каждом шаге работы МТ передвигается вдоль ленты памяти на 1 ячейку влево, вправо или остается на месте. Движение автомата будем обозначать элементами множества движений D = {L,R,N}.

3.Считывающая головка, которая на любом шаге работы МТ просматривает какую-либо ячейку памяти.

4.Устройство управления (управляющее устройство), которое на каждом шаге работы МТ может

находиться в одном из состояний, множество Q = {q1, q2, ..., qn} которых конечно и называется внутренним алфавитом. В каждый момент времени машина Тьюринга может находиться только в одном из этих состояний.

Работа МТ может быть описана следующим образом:

1.В начальный момент работы МТ лента памяти находится в начальном состоянии (конечное непустое слово на ленте называется входным словом), автомат находится в начальном состоянии q1 и считывающая головка просматривает самый левый непустой символ входного слова.

2.На каждом шаге работы МТ головка считывает символ ai A из просматриваемой ячейки и в

зависимости от него и от состояния qj из Q устройства управления автомат:

a) при необходимости меняет символ ai (записывает новый символ на позицию i);

b) при необходимости меняет состояние устройства управления (записывает новое состояние на позицию j);

c) при необходимости осуществляет движение в направлении d из D (или остается на месте);

3.Если в результате предыдущих шагов автомат переходит в такое состояние, при котором:

a)состояние автомата не меняется,

b)символ в просматриваемой ячейке не меняется,

c)движение автомата вдоль ленты памяти не происходит,

то машина переходит в заключительное состояние останова. Для упрощения такое состояние обозначим через q0. а переход к нему будем обозначать как переход к состоянию q0.

Это состояние мы также включим в множество состояний Q ={q0, q1, ..., qn}. Слово, которое получается при переходе МТ к состоянию останова, будем называть выходным словом.

Все действия в машине Тьюринга выполняются в соответствии с заданной программой. Программа представляет собой конечный набор команд типа ciqj ckqrd, где d D. Если головка просматривает ячейку, в которой находится символ qj и в программе машины Тьюринга есть команда ciqj ckqrd, символ в просматриваемой ячейке заменяется на ck, машина переходит в состояние qr и головка остается на месте, если d = N, сдвигается на ячейку вправо или влево, если d = L или d = R. Далее машина переходит к следующему такту. Если после очередного перехода в программе не остается команды, в левой части которой находится ciqj, машина останавливается.

Функция называется вычислимой, если существует машина Тьюринга, которая ее вычисляет.

Справедливо и обратное утверждение: если функция вычислима, то существует машина Тюринга, которая ее вычисляет.

Пример машины Тюринга:

На ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова.

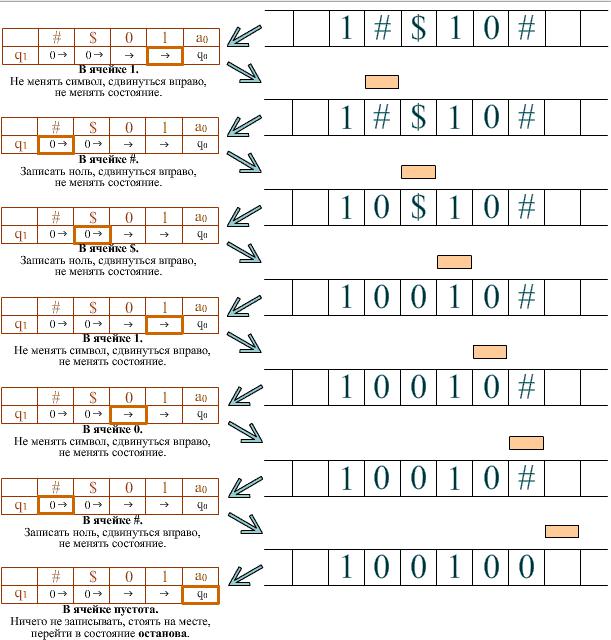
В детерминированной машине Тюринга каждая пара ciqj встречается в левых частях команд не больше одного раза.

Пусть П – некоторая массовая задача, характеризуемая множеством параметров. Пусть I П – индивидуальная задача, в которой эти параметры фиксированы. Пусть с массовой задачей П связана и зафиксирована схема кодирования α, которая ставит каждой индивидуальной задаче I П в соответствие слово α(I) в некотором алфавите A. При этом под размерностью задачи I понимается длина слова α(I). Пусть Т – машина Тьюринга, решающая задачу П и tT(n) = max (tT(I)) – максимальная сложность. Говорят, что машина T решает задачу П за полиномиальное время, если tT(n) = O(p(n)) для некоторого полинома р. В противном случае говорят, что машина T решает задачу П за экспоненциальное время. Про задачу П говорят, что она разрешима за полиномиальное время, если существует машина Тьюринга Т, решающая ее за полиномиальное время. Класс задач, разрешимых за полиномиальное время, относится к классу сложности P.

Экспоненциальные алгоритмы часто оказывается неприемлемыми из-за низкой эффективности и соответственно высокой ресурсоемкости для задач большой размерности. Здесь под ресурсоемкостью понимается как время выполнения, так и память, потребляемая во время выполнения алгоритма. В связи с этим задачи, для которых не удается построить полиномиальные алгоритмы, являются труднорешаемыми. К числу труднорешаемых задач относятся в том числе и задачи распознавания, в которых необходимо установить существование определенного свойства.

Так, для задачи коммивояжера соответствующая задача распознавания коммивояжера формулируется следующим образом: задано конечное множество городов и расстояний между ними, а также ограничение длины маршрута B; существует ли маршрут объезда всех городов, длина которого не превосходит B?

Анализ труднорешаемых задач распознавания показывает, что для каждой задачи существует множество вариантов при положительном ответе надо угадать удачный вариант (то есть выбрать недетерминированно), а затем проверить выполнение свойства за полиномиальное число шагов. Класс таких задач называется классом задач с недетерминированно-полиномиальными алгоритмами, или классом NP, в отличие от класса задач распознавания, для которых существуют полиномиальные алгоритмы и который называется классом P.

Смысл введения класса NP задач состоит в выявлении таких задач этого класса (мы назовем их NP-полными), для которых существование полиномиального алгоритма для решения одной из них означает, что для любой такой задачи также можно построить полиномиальный алгоритм ее решения. Поэтому в тех случаях, когда для некоторой задачи не удается построить полиномиальный алгоритм, пробуют доказать, что она является NP-полной. Если это удается, то попытки построить полиномиальный алгоритм ее решения следует прекратить, поскольку существование такого эффективного алгоритма означает, что любая другая задача из класса NP также может быть решена эффективным полиномиальным алгоритмом.

Классу NP можно дать более строгое определение. Рассмотрим некоторую произвольную задачу Π распознавания свойства Q. Обозначим через DΠ область определения массовой задачи Π, а через I DΠ – конкретизированную задачу с конкретными фиксированными данными. Определим YΠ как множество конкретизированных задач, имеющих ответ "да". Неформальное определение класса NP можно дать с помощью недетерминированного алгоритма, состоящего из двух этапов:

1)угадывание;

2)проверка.

На первой стадии в рамках решения конкретизированной задачи I DΠ происходит «угадывание» некоторой структуры S (варианта), а затем I и S подаются совместно на второй этап, то есть проверки, которая выполняется детерминированным способом и либо заканчивается ответом "да" или "нет", либо проверка неограниченно продолжается. Последние две возможности мы не будем различать.

Недетерминированный алгоритм «решает» задачу распознавания Π, если для любой конкретизированной задачи I DΠ выполнены условия:

1.Если I YΠ, то существует структура S, угадывание которой для входных данных I приводит к тому, что стадия проверки с входными данными (I, S) заканчивается ответом "да".

2.Если I YΠ, то не существует такой структуры S, угадывание которой для входных данных I приводит к тому, что стадия проверки с входными данными (I, S) заканчивается ответом "да".

Недетерминированный алгоритм, решающий задачу Π, работает в течение «полиномиального времени», если найдется догадка S, которая на этапе детерминированной проверки с входными данными (I, S) приводит к ответу "да" за время p(l(I)), где p – полином, а l(I) – объем входных данных задачи I. Такой алгоритм мы будем называть недетерминированно-полиномиальным.

Класс NP – это класс всех задач распознавания, которые могут быть решены недетерминированно-полиномиальными алгоритмами.

Отметим отличие от детерминированных алгоритмов. Если рассматривается задача класса P, то ее частная задача A: «Дано I; верно ли, что выполняется свойство Q?» – может быть решена детерминированным алгоритмом за полиномиальное время. Но также за полиномиальное время детерминированным алгоритмом может быть решена и задача B: «Дано I; верно ли, что не выполняется свойство Q?». Для класса NP такой симметрии нет: для задачи A достаточен пример (вариант), и решение примера также идет за полиномиальное время, а для задачи B нужно перебирать все варианты, чтобы удостовериться в отсутствии свойства Q, а это требует уже экспоненциального времени для детерминированного алгоритма.

Понятие недетерминированного алгоритма можно ввести с помощью недетерминированной машины Тьюринга. Ее модель похожа на модель рассмотренной ранее детерминированной машины Тьюринга со следующими отличиями:

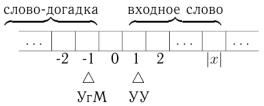
1.Недетерминированная машина Тьюринга имеет угадывающий модуль, головка которого только записывает информацию на ленту (слово-догадку). Угадывающий модуль в "активном" состоянии на каждом шаге своей работы совершенно произвольно либо записывает в обозреваемую ячейку любой символ внешнего алфавита Γ и сдвигается на одну ячейку влево, либо останавливается и переходит в "пассивное" состояние.

2.Устройство управления имеет 2 режима работы, а именно "пассивный", когда угадывающий модуль находится в "активном" состоянии, и "активный", когда угадывающий модуль переходит в "пассивное" состояние. Множество состояний устройства управления включает начальное

состояние, 2 заключительных состояния q0Y (вычисления закончились ответом "да") и q0N (вычисления закончились ответом "нет") и другие состояния алгоритма.

УгМ – угадывающий модуль; УУ – устройство управления

Работа недетерминированной машины Тьюринга в отличие от работы детерминированной машины Тьюринга имеет 2 различные стадии, и ее можно описать следующим образом:

1.В начальный момент входное слово x записывается в ячейки с номерами 1, 2, . . . , |x| и головка устройства управления смотрит на ячейку с номером 1, а головка угадывающего модуля – на ячейку с номером -1 (см. рис. выше). При этом устройство управления "пассивно" (находится в "пассивном" режиме), а угадывающий модуль находится в активном состоянии.

2.Стадия угадывания: угадывающий модуль начинает работать, формируя слово-догадку, которым может быть произвольное слово из Γ (любое слово внешнего алфавита или пустое

слово). Работа угадывающего модуля может продолжаться неограниченно – это также соответствует ответу "нет" недетерминированного алгоритма. Как только угадывающий модуль остановится и перейдет в "пассивное" состояние (слово-догадка сформировано), устройство управления переходит в активный режим.

3.Стадия проверки: начинается с перехода устройства управления в "активный" режим (в этот момент оно находится в состоянии q1) и осуществляется функцией перехода δ, которая определяет записываемый символ в обозреваемую ячейку, изменение состояния и движение автомата вдоль ленты. Таким образом, работа на этапе проверки осуществляется так же, как и для детерминированной машины Тьюринга (угадывающий модуль и его головка в этом вычислении не участвуют). Во время стадии проверки устройство управления может обозревать любые ячейки, в том числе ячейки входного слова и ячейки слова-догадки, сформированного на предыдущей стадии.

4.Вычисления заканчиваются тогда, когда устройство управления перейдет в одно из двух заключительных состояний. Вычисление называется принимающим, если оно заканчивается

состоянием q0Y. Во всех других случаях вычисление называется непринимающим (заканчивается состоянием q0N или не заканчивается совсем).