4. Исследование линеаризованной математической модели

Рассмотрим систему, представленную в канонической форме Коши:

,

где

Для линеаризации выбрали статический режим , в окрестности которого проводится линеаризация. А именно выбрали точку

.

Далее определили матрицы частных производных:

– матрица состояний

– матрица входов

– матрица выходов

– матрица обхода

Матрицы имеют постоянные коэффициенты, зависящие от статического режима.

В итоге, получили систему

Здесь переменные и называются приращениями (или отклонениями) переменных и относительно значений и .

СНДУ, записанные в форме Коши:

Уравнения выходов:

Как выходы в данной системе заданы ток возбуждения и угловая скорость .

;

;

;

= ;

=

Уравнения f(x,u):

Текст программы:

%%lab4

clc

clear

%%исходные данные

global Ucn Uvn Ce r_j r_v w l_j J k Cm Mcn Wn Potokn In p p2 a10 a11 a20 a21 a22 a23 a30 a31 a32 b1 b2

potok=[0;0.35;0.57;0.72;0.83;0.91;0.97;1.01;1.06;1.07];

F=[0;0.1318;0.2636;0.3954;0.5272;0.659;0.7909;0.9227;1.0545;1.1863];

Ucn=220;% напряжение сети ном

Uvn=220; % напряжение возбуждения

Ce=205;

r_j=0.3; %сопротивление якоря

r_v=145; %сопротивление возбуждения

w=4000; %витки

l_j=0.1; %индуктивность якоря

J=0.35; %момент инерции

k=4000;

%%номинальные данные

Cm=200;

Mcn=50;%номинальный поток сопротивления

Wn=100;%обороты номинальные

Potokn=0.007;%номинальный поток, Вб

In=50;%номинальный ток двигателя

%%полином 5 степени

p=[0.6010 0 -0.1446 0 0.4384 0];

p2=polyder(p);

a10 = Uvn/(Potokn*w);

a11 = Uvn;

a20 = 1/(In*l_j);

a21 = Ucn;

a22 = Ce*Wn*Potokn;

a23 = In*r_j;

a30 = 1/(Wn*J);

a31 = Cm*Potokn*In;

a32 = Mcn;

b1 = Uvn/r_v*w;

b2 = Wn;

%% Uc+20%

t = [0:0.01:6];

x0=[0; 0; 0];

u1 = 0.2; u2 = 0;

u = [u1*ones(size(t)); u2*ones(size(t))];

x = [1.04; 0.22; 0.463];

P = polyval(p2,x(1));

%%матрицы A B C D

A = [-a10*P, 0, 0; -a22*a20*x(3), -a23*a20, -a22*a20*x(1); a30*a31*x(2),a30*a31*x(1), 0];

B = [0, 0; a21*a20, 0; 0, -a32*a30];

C = [b1*P, 0, 0; 0, 0, b2];

D = [0,0;0, 0];

[Y, X] = lmsim(A,B,C,D,t,x0,u);

figure(1); hold on; plot(t,(X(3,:)+x(3))); grid on; xlabel('t,с');ylabel('W, об/мин');

figure(2); hold on; plot(t,(X(2,:)+x(2))); grid on; xlabel('t,с');ylabel('iд, А');

figure(3); hold on; plot(t,(X(1,:)+x(1))); grid on; xlabel('t,с');ylabel('Ф, Вб');

figure(4); hold on; p = poly(A); lmd = roots(p); xlabel('Re');ylabel('Im');

plot(real(lmd),imag(lmd),'*'); grid on;

%% Uc-20%

t = [0:0.01:6];

x0=[0; 0; 0];

u1 = -0.2; u2 = 0;

u = [u1*ones(size(t)); u2*ones(size(t))];

x = [1.04; 0.22; 0.463];

P = polyval(p2,x(1));

%%матрицы A B C D

A = [-a10*P, 0, 0; -a22*a20*x(3), -a23*a20, -a22*a20*x(1); a30*a31*x(2),a30*a31*x(1), 0];

B = [0, 0; a21*a20, 0; 0, -a32*a30];

C = [b1*P, 0, 0; 0, 0, b2];

D = [0,0;0, 0];

[Y, X] = lmsim(A,B,C,D,t,x0,u);

figure(1); hold on; plot(t,(X(3,:)+x(3))); grid on; xlabel('t,с');ylabel('W, об/мин');

figure(2); hold on; plot(t,(X(2,:)+x(2))); grid on; xlabel('t,с');ylabel('iд, А');

figure(3); hold on; plot(t,(X(1,:)+x(1))); grid on; xlabel('t,с');ylabel('Ф, Вб');

Функция lmsim:

function [y,x]=lmsim(a,b,c,d,t,x0,u)

%

% simulation of linear system

%

% dx(t)/dt=Ax(t)+Bu(t)

% y(t)=Cx(t)+du(t)

%

% x(0)=x0

%

% t - vector-string of simulation time

% x0 - vector-column of initial conditions

% u - matrice of controls (number of columns is equal to length of vector t

% number of strings is equal to number of outputs)

%

%

h=t(2)-t(1);

% matrix exponent

[m,n] = size(a);

[m,nb] = size(b);

s = expm([[a b]*h; zeros(nb,n+nb)]);

p = s(1:n,1:n);

g= s(1:n,n+1:n+nb);

%

% time process

%

x=(ltitr(p,g,u',x0'))';

y=c*x+d*u;

Результаты реализации программы и моделирования приведены на Рис.15-22.

Динамический режим(+20%Uc)

Переходные процессы переменных состояния:

Рис.15 – Сравнение магнитного потока линеаризованной(слева) и нелинейной систем

Рис.16 – Сравнение тока двигателя линеаризованной (слева) и нелинейной систем

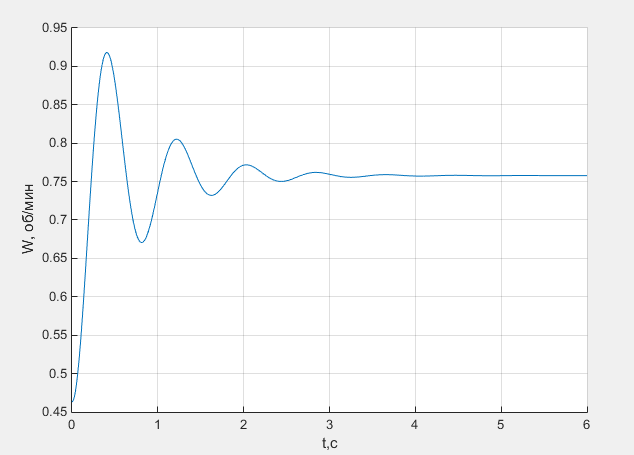
Рис.17 – Сравнение скорости вращения двигателя линеаризованной (слева) и нелинейной систем

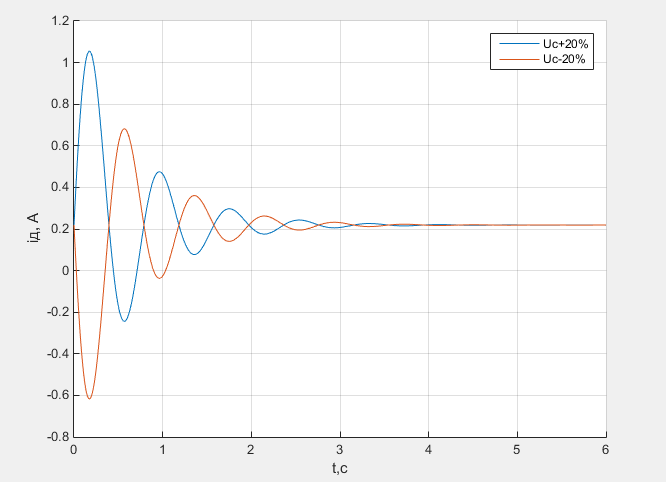
Рис.18 – График изменения тока двигателя при изменении входного воздействия на +/- 20%

Рис.19 – График изменения скорости двигателя при изменении входного воздействия на +/- 20%

Переходные процессы выходных значений (ток возбуждения и угловая скорость):

Рис.20 – Переходный процесс тока возбуждения

Рис.21 – Переходный процесс угловой скорости

Рис.22 – Корни полинома матрицы А

Переходные процессы полученной линеаризованной системы сходятся с результатами переходных процессов нелинейной системы с небольшими отклонениями. Система является устойчивой по Ляпунову, т.к. вещественные части всех собственных чисел матрицы А являются отрицательными.