2. Исследование переходных процессов динамической системы
Для исследования характера переходных процессов с использованием численного интегрирования СНДУ объекта необходимо выполнить следующие задачи:
Преобразовать исходные уравнения к нормированному виду;
Построить по полученным уравнениям схему в среде SIMULINK и получить переходные процессы;
Изменить входной параметр Uc на ±20% и привести изменившиеся переходные процессы;
Построить фазовые траектории.
Исходные уравнения:
F=iвW, Ф=Л(F);
Преобразованные уравнения:
Рис.3. Схема в среде SIMULINK
Динамика (номинальный режим):
Рис.4. Поток
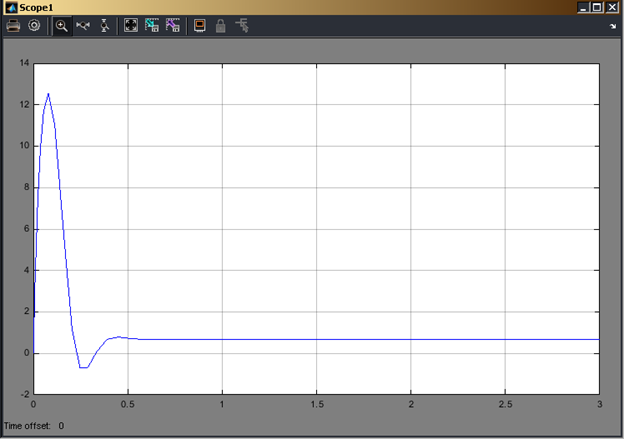
Рис.5. Ток
Рис.6. Угловая скорость
Изменение входного параметра Uc на ±20%:
Рис.7. Схема в среде SIMULINK
Рис.8. Ток двигателя при изменении входного параметра на +20%
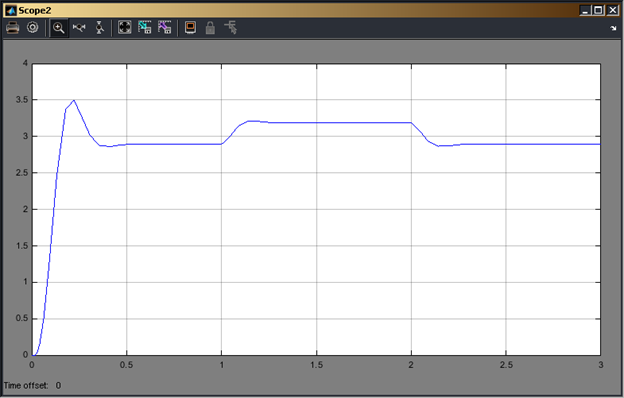
Рис.9. Угловая скорость при изменении входного параметра на +20%
Рис.10. Ток двигателя при изменении входного параметра на -20%
Рис.11. Угловая скорость при изменении входного параметра на -20%
Фазовые траектории:
Рис.12. Зависимость скорости от потока
Рис.13. Зависимость тока от скорости
По результатам моделирования видно, что при изменении входящего воздействия на ±20% на графиках тока и угловой скорости появились заметные скачки, график потока не меняется, так как не зависит от входного напряжения.
3. Исследование статических режимов динамической системы
Статический режим будет описывать система алгебраических уравнений, т.е. уравнений, куда не входят производные, так как последние в статическом режиме равны нулю. Все статические режимы могут быть описаны СНЛАУ, записанной в обобщенной форме относительно компонент векторов 𝑢 и 𝑥:
Система уравнений, описывающая динамическую систему:
В статическом режиме:
Исключим уравнения, не содержащие переменные состояния:
Произведем нормирование всех переменных входа и выхода:
Заменим входные и выходные переменные и коэффициенты перед ними:
;
;
После всех подстановок получили:
Для реализации метода Ньютона найдем матрицу частных производных:
Текст программы:
%%lab3
clc
clear
%%исходные данные
Ucn=220;% напряжение сети ном
Uvn=220; % напряжение возбуждения
Ce=205;
r_j=0.3; %сопротивление якоря
%%номинальные данные
Cm=200;
Mcn=50;%номинальный поток сопротивления
Wn=100;%обороты номинальные
Potokn=0.007;%номинальный поток
In=50;%номинальный ток двигателя
global a21 a22 a23 a31 a32 p p2
%%коэффициенты для матриц
a21 = Ce*Potokn*Wn;
a22 = In*r_j;
a23 = Ucn;
a31 = Cm*Potokn*In;
a32 = Mcn;
%%полином 5 степени и его производная
p=[0.6010 0 -0.1446 0 0.4384 0];
p2=polyder(p);
%%векторы начальных значений
x01=[1;1;1];
x02=[1;1;1];
x03=[1;1;1];
u=0.2:0.2:1.2;
u1=[u;ones(1,length(u));ones(1,length(u))];
u2=[ones(1,length(u));u;ones(1,length(u))];
u3=[ones(1,length(u));ones(1,length(u));u];
e=0.001;%точность метода
xx=[];
xx2=[];
xx3=[];
for i=1:length(u)
x1=newton('fun_F', 'fun_G', x01, u1(:,i),e);
xx=[xx x1];
x01=x1;
x2=newton('fun_F', 'fun_G', x02, u2(:,i),e);
xx2=[xx2 x2];
x02=x2;
x3=newton('fun_F', 'fun_G', x03, u3(:,i),e);
xx3=[xx3 x3];
x03=x3;
end
%%графики
subplot(311)
plot(u1(1,:),xx(1,:),'r--',u1(1,:),xx(2,:),'g--',u1(1,:),xx(3,:),'b'),grid
legend('Ф норм','i норм','w норм')
xlabel('Mc')
ylabel('Ф норм , i норм, w норм')
subplot(312)
plot(u2(2,:),xx2(1,:),'r--',u2(2,:),xx2(2,:),'g--',u2(2,:),xx2(3,:),'b'),grid
legend('Ф норм','i норм','w норм')
xlabel('Uc')
ylabel('Ф норм , i норм, w норм')
subplot(313)
plot(u3(3,:),xx3(1,:),'r--',u3(3,:),xx3(2,:),'g--',u3(3,:),xx3(3,:),'b'),grid
legend('Ф норм','i норм','w норм')
xlabel('Uв')
ylabel('Ф норм , i норм, w норм')
Функция левых частей СНЛАУ:
function [ F ] = fun_F( x,u )
global a21 a22 a23 a31 a32 p
P=polyval(p, x(1));
F=[u(3) - P; a21*x(1)*x(3) + a22*x(2)-a23*u(2); a31*x(1)*x(2)-a32*u(1)];
end
Функция матрицы частных производных:
function [ G ] = fun_G(x,u)
global a21 a22 a31 p2
P=polyval(p2, x(1));
G=[-P, 0, 0;a21*x(3), a22, a21*x(1);a31*x(2), a31*x(1), 0];
end
Функция, реализующая метод Ньютона:
function [x] = newton( F,G,x0,u,e )
F2=feval(F,x0,u);
G2=feval(G,x0,u);
x=x0;
while(norm((G2^-1)*F2) > e)
x=x-(G2^-1)*F2;
F2=feval(F,x,u);
G2=feval(G,x,u);
end
end
График зависимости переменных состояния от изменения входных величин приведен на Рис.14.
Рис.14. График зависимости переменных состояния от изменения входных величин
Исходя из Рис.14 можно сказать, что при изменении момента сопротивления Mc магнитный поток Ф не меняется, скорость вращения падает, а ток двигателя растёт. При изменении входного напряжения UC магнитный поток Ф и ток двигателя не меняются, а скорость вращения растёт. Такие процессы обусловлены механическими и электромеханическими характеристиками ДПТ независимого возбуждения.