
лабораторные / ЛР 3
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра КСУ
отчёт
по лабораторной работе №3
по дисциплине «Математическое моделирование объектов и систем управления»
Тема: Анализ устойчивость динамических систем средствами MATLAB
Вариант 1
Студенты гр. 6408 |
|
Нуртазин И. |
|
|
Попов М.М. Лукьянцов К. В. |
Преподаватель |
Шпекторов А.Г. |
Санкт-Петербург
2020
Цель работы: 1 – Сформировать ss-объект, соответствующий LTI – модели самолета со входом u= (δe δn F)T и выходом y
2 - Замкнуть объект данным регулятором
3- При значении k3=0,799 проверить устойчивость с использованием второго метода Ляпунова. Построить диаграмму расположения полюсов на комплексной плоскости.
4- Найти область устойчивости по параметру к3
Задание:
Объект управления – пассажирский самолет Боинг-747, который управляется в боковом движении с помощью руля направления и элеронов: их отклонения от нейтрального положения обозначены как n и e соответственно. В вектор состояния входят следующие компоненты: vz – скорость бокового сноса; y – угловая скорость по рысканию; x – угловая скорость по крену; – угол рыскания; – угол крена; z – боковой снос. Система линейных дифференциальных уравнений, описывающих процесс стабилизации самолета в боковом движении при посадке, имеет следующий вид:
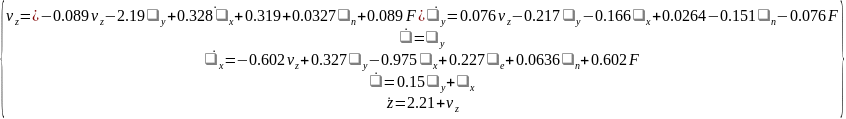
Регулятор:
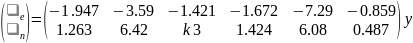
Содержание работы:
Сформировать SS-объект
Общий вид:
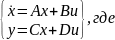
А – Матрица состояний, В – Матрица входов, С - Матрица выхода, D – Матрица обхода.
За переменные состояний возьмем следующий порядок:
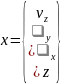
Выходами данного объекта будут следующими:
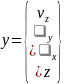
Входы данного объекта равны:
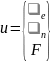
Матрицы А, В, С, D равны
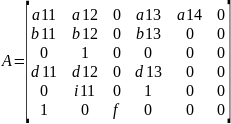
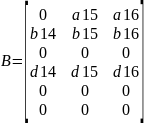
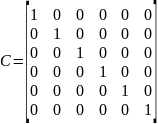
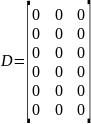
Где
-
a11=-0.089;
a12=-2.19;
a13=0.328;
a14=0.319;
a15=0.0327;
a16=0.089;
b11=0.076;
b12=-0.217;
b13=-0.166;
b14=0.0264;
b15=-0.151;
b16=-0.076;
d11=-0.602;
d12=0.327;
d13=-0.975;
d14=0.227;
d15=0.0636;
d16=0.602;
i11=0.15;
f=2.21;
Графически данный объект можно представить следующим образом:
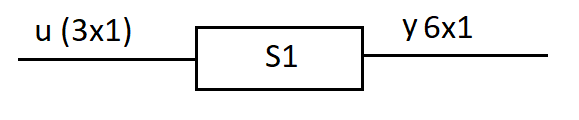
Рис.1. Графическое представление объекта ss.
Создадим объект регулятора:
Матрицы А, B, C – нет, матрица D равна:
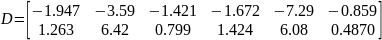
Для замыкания объектов используется функция lft, данная функция замыкает первые указанные выходы второго объекта, с последними входами первого объекта, и последние указанные выходы первого объекта, с первыми входами второго объекта. Что бы получить нужное замыкание, необходимо изменить порядок столбцов в матрице В первого объекта.
После преобразования в первом объекте, порядок входов стал:
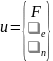
Графически можно изобразить следующим образом:
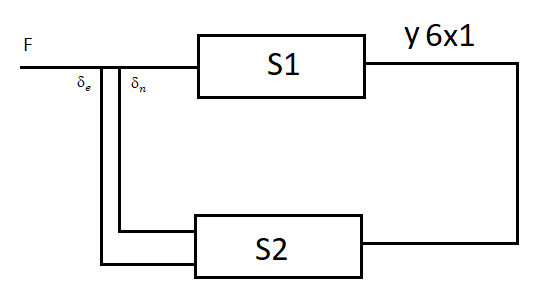
Рис.2.Замыкание объекта и регулятора.
Проверим устойчивость с использованием второго метода Ляпунова при k3=0.799.
Метод Ляпунова состоит в решении уравнения вида:
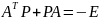
Где Р – неизвестная, Е – единичная матрица размером матрицы А (nxn)
Затем вычислить ведущие миноры матрицы Р, если все миноры >0, то система асимптотически устойчива.
В матлабе для нахождения матрицы Р используется функция Р=lyap(A,E). Матрица P выглядит следующим образом:

Все ведущие миноры матрицы Р > 0, следовательно, система асимптотически устойчива.
![]()
Рис.4. Ряд из миноров матрицы Р.
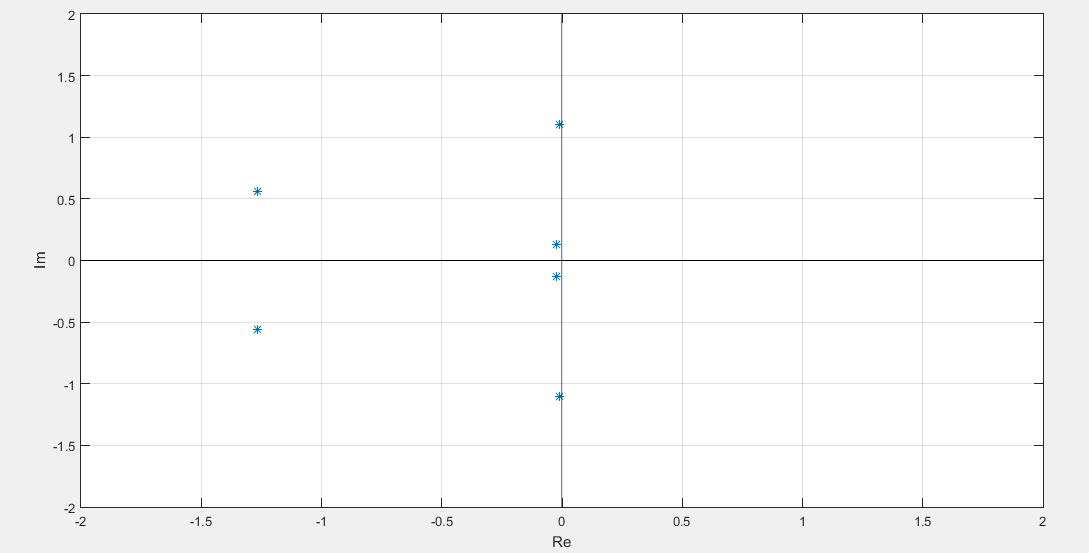
Рис.5. Расположение полюсов на комплексной плоскости
4. Найти область устойчивости по k3
Для этого создадим множество ss объектов с разным параметром k3. Используем диапазон [-10:0.1:50]. Для каждого объекта найдем максимальный (наибольший) вещественный корень, если этот корень <0 – то и все корни матрицы А <0, следовательно система устойчива, если же максимальный корень >0 – система неустойчива. Ниже представлены максимальные вещественные корни при разных k3 от -10 до 100 с шагом 0,1.
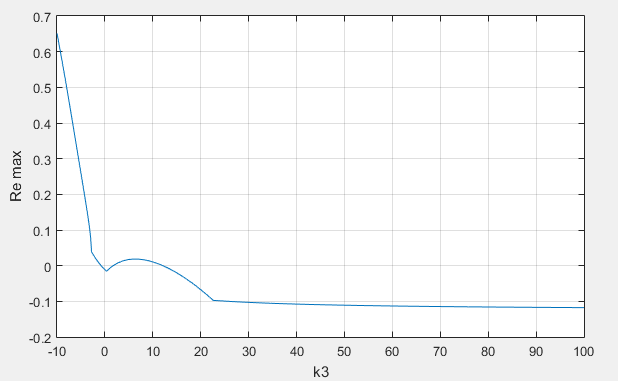
Рис.6. Максимальная вещественная часть от k3
Область устойчивость данной системы располагается ниже 0 по оси Re max.
Код программы:
clear,clc; a11=-0.089; a12=-2.19; a13=0.328; a14=0.319; a15=0.0327; a16=0.089; b11=0.076; b12=-0.217; b13=-0.166; b14=0.0264; b15=-0.151; b16=-0.076; d11=-0.602; d12=0.327; d13=-0.975; d14=0.227; d15=0.0636; d16=0.602; i11=0.15; f=2.21;
|
Продолжение A=[a11, a12, 0, a13, a14, 0; b11, b12, 0, b13, 0, 0; 0, 1, 0, 0, 0, 0;... d11, d12, 0, d13, 0, 0; 0, i11, 0, 1, 0, 0; 1, 0, f, 0, 0, 0]; B=[0, a15, a16; b14, b15, b16; 0, 0, 0; d14, d15, d16; 0, 0, 0; 0, 0, 0]; C=eye(6); D=[0, 0, 0;0, 0, 0;0, 0, 0;0, 0, 0;0, 0, 0;0, 0, 0]; S1=ss(A,B,C,D); DD=[-1.947, -3.59, -1.421, -1.672, -7.29, -0.859; 1.263, 6.42, 0.799, 1.424, 6.08, 0.487]; S2=ss(DD); set(S1,'B',[B(:,3),B(:,1),B(:,2)]); S=lft(S1,S2,2,6); set(S,'C', [0, 0, 0, 0, 1, 0], 'D',[0]); P=lyap(S.A,eye(size(S.A))); q=[]; for i=1:6 %цикл составляет ряд из миноров матрицы P q=[q det([P(1:i,1:i)])]; i=i+1; end rooots=roots(poly(S.A)); plot(real(rooots),imag(rooots),'*') %построение полюсов grid on hold on t=[-2:2]; x=0*t; plot(t,x,'black'); plot(x,t,'black'); % строит оси hold off k=[]; N=[]; for i=-10:0.1:100 % цикл создает ряд наибольших вещественных корней объекта REZ DD2=[-1.947, -3.59, -1.421, -1.672, -7.29, -0.859; 1.263, 6.42, i, 1.424, 6.08, 0.487]; S3=ss(DD2); REZ=lft(S1,S3,2,6); k=[k i]; N=[N max(real(eig(REZ)))]; end figure(2); plot(k,N); grid on
|
Выводы: На основе предыдущей работы был сформирован ss объект, с помощью метода Ляпунова была проверена устойчивость этого объекта. Так же с помощью программного кода можно найти область значений параметра регулятора, где система будет устойчивой.
Практическая часть
Дано: система линейных алгебраических уравнений
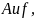
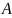 – известная
матрица,
– известная
матрица,
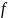 – известный вектор правой части,
– известный вектор правой части,
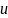 – точное решение (недостижимое),
обращающее уравнение в тождество.
– точное решение (недостижимое),
обращающее уравнение в тождество.
Вместо точного решения вводится вектор y приближенного решения, вычисляемого итерационно.
Невязка на k-м шагу – мера приближения численного решения к точному:
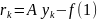
Поправка – взвешенная невязка:
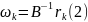
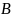 – весовая
матрица простой структуры (диагональная),
при удачном выборе увеличивает скорость
метода (по умолчанию можно принять
единичной);
– весовая
матрица простой структуры (диагональная),
при удачном выборе увеличивает скорость
метода (по умолчанию можно принять
единичной);
Погрешность: ошибка численного решения
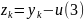
Заданием на практическую работу был трёхслойный градиентный метод. В трехслойном методе решение вычисляется по значениям двух предыдущих итераций. Итерационные формулы имеют вид:
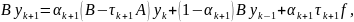
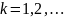
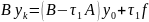
А
итерационные параметры
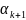 и
и
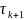 находятся по формулам:
находятся по формулам:
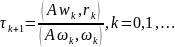
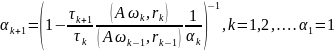
Вывод: За 8 итераций мы нашли решение удовлетворяющей нас точности.
Код практической работы:
clear, clc
rng(08), A1= rand(4);
Alpha = 1;
f1 = [1 2 3 4];
f1 = f1';
A=A1'*A1;
f=A1'*f1;
B = eye(4);
y0 = [1; 1; 1; 1];
r0=A*y0-f;
w0=B\r0;
C1=(A*w0)';
tau1 = (C1*r0)/(C1*w0)
y1=B\(B-tau1*A)*y0+B\(tau1*f);
n=0;
while norm (r0)>0.001
r1=A*y1-f;
w1=B\r1;
C=(A*w1)';
tau2 = (C*r1)/(C*w1)
Alpha = inv((1-((tau2/tau1)*((C*r1)/(C1*r0))*(1/Alpha))))
y2=B\((Alpha*B-Alpha*tau2*A)*y1)+B\((1-Alpha)*B*y0)+B\(Alpha*tau1*f)
tau1=tau2;
r0=r1;
w0=w1;
y0=y1;
y1=y2;
C1=C;
n=n+1
end
