лабораторные / Лаб6. Нуртазин, Попов, Лукъянцов

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра КСУ

отчёт

по лабораторной работе №6

по дисциплине «Математическое моделирование объектов и систем управления»

Тема: Исследование хаотических систем

Вариант 1

Студенты гр. 6408		Нуртазин И.
		Попов М.М. Лукьянцов К. В.
Преподаватель		Шпекторов А.Г.

Санкт-Петербург

2020

Цель работы: ознакомиться с классом хаотических систем, освоить средства MATLAB для моделирования «странных аттракторов», изучить практические способы определения параметров хаотических систем.

Задание: определить старший показатель Ляпунова для аттрактора Айзавы двумя способами.

Исходные данные: Аттрактор Айзавы:

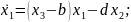
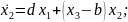
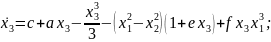
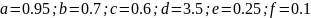
Ход работы: для начала мы ввели исходные данные и уравнения. После этого построим аттрактор Айзавы (начальные условия выставлены 1/1/1). Он представлен на рисунке 1.

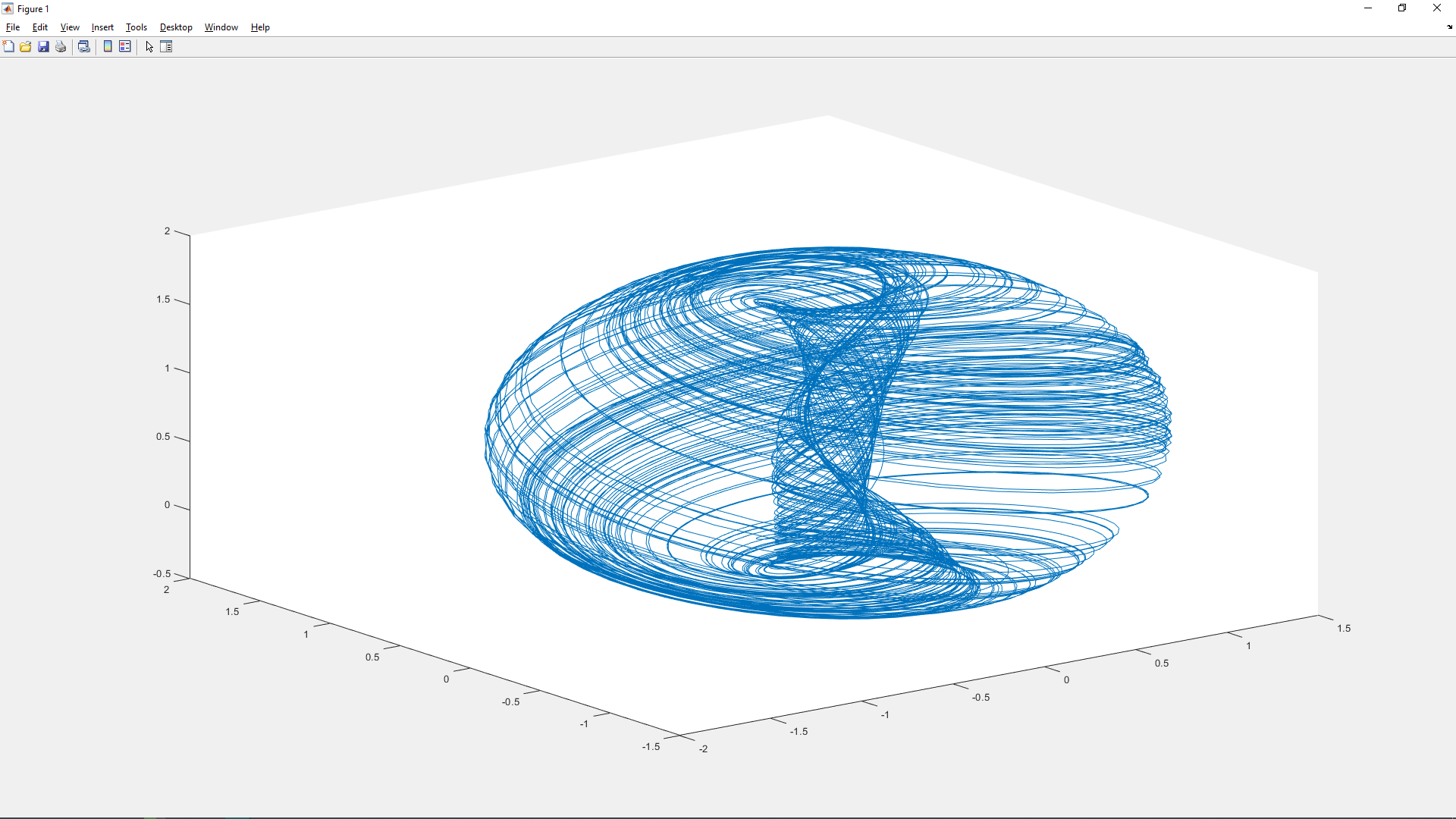
Рис. 1 – Аттрактор Айзавы.

Возьмём за начальные условия значения, которые принадлежат нашему аттрактору, полученному ранее. Этими числами являются [-0.1387; -0.2527; 1.3259].

1. Первый способ определения старшего показателя Ляпунова (далее СПЛ) основан на анализе уравнений хаотической системы. За начальные условия мы уже приняли значения, которые принадлежат нашему аттрактору.

Теперь найдём матрицу линеаризации. Для этого нам нужны частные производные уравнений:

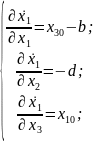
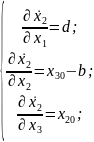
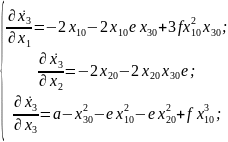
Далее нам необходимо составить матрицу собственных чисел, причём СПЛ определяется как максимальное значение собственного числа (Рисунок 2).

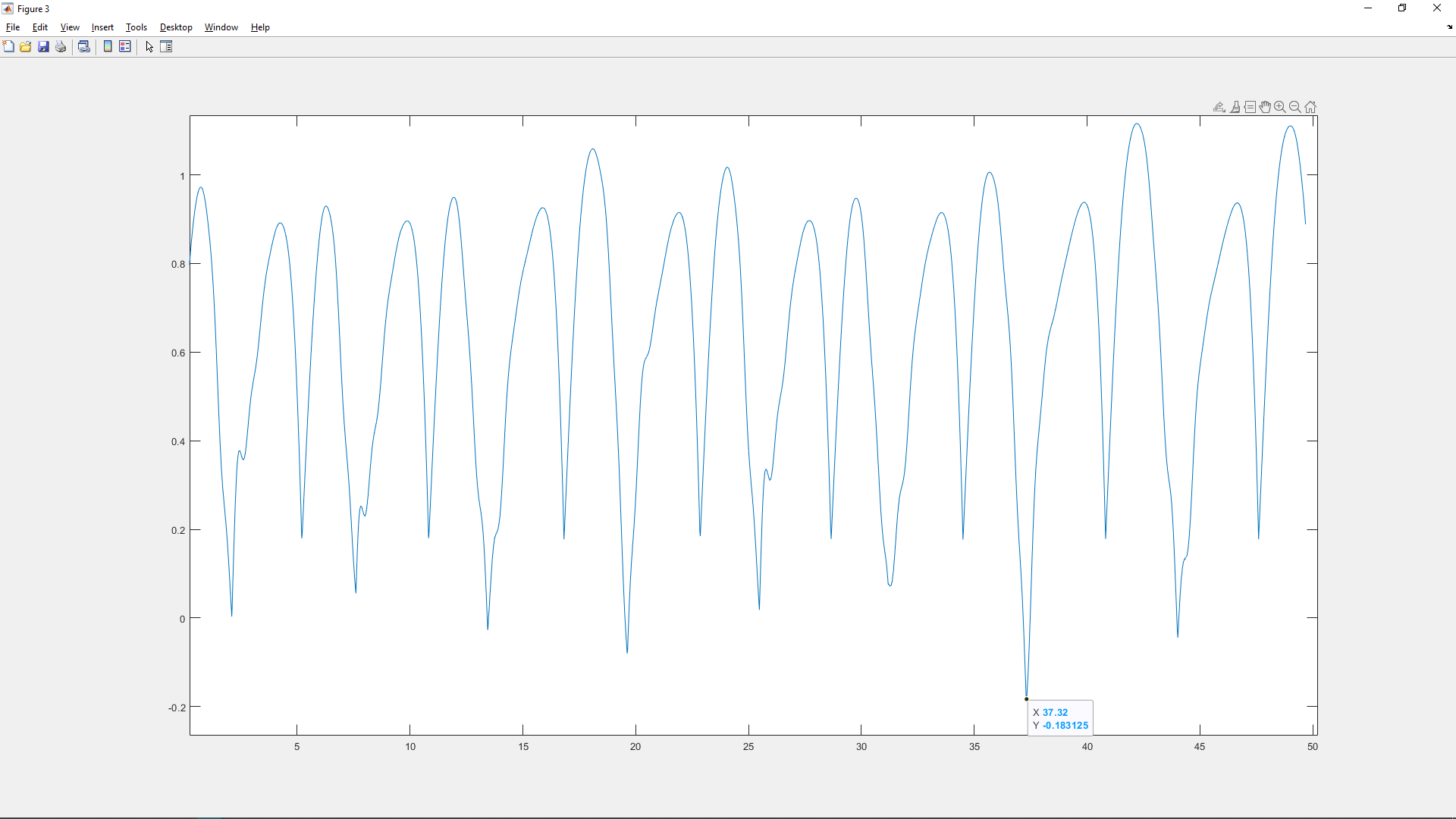
Рис.2 – СПЛ

Возьмём отмеченную отрицательную точку на проверку устойчивости системы. Числовое значение по Х у него 37.32, найдём его в векторе-строке t. Проверим на устойчивость. Корни матрицы А для этой траектории представлены на рисунке 3.

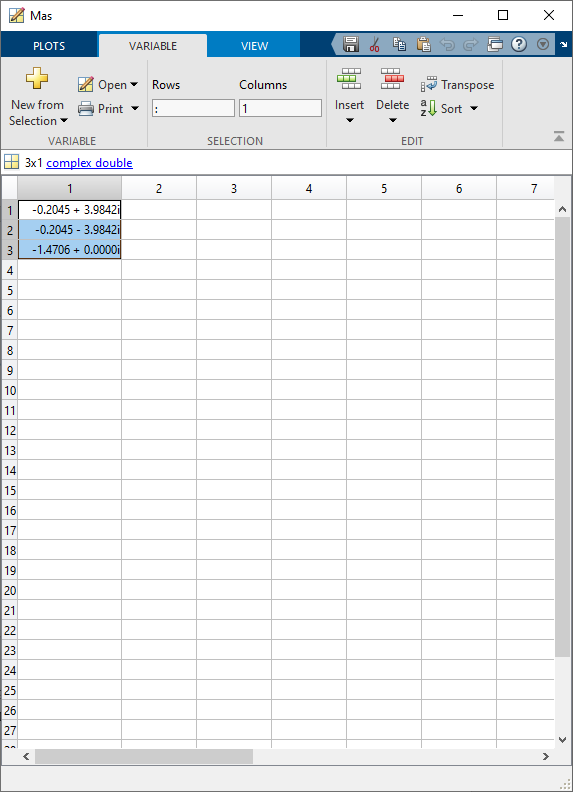
Рис. 3 – корни матрицы А для конкретной траектории.

2. Второй способ определения СПЛ основан на анализе решений системы исходных уравнений.

Для этого мы добавили малую величину 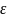к одной из координат начальной точки траектории. Создадим сетку рассогласования траекторий 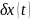и рассчитаем .

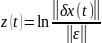На рисунках 4 и 5 показаны графики .

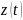При добавлении к первой координате мы получили коэф. наклона равные 0.1254, 0.1154, 0.1268. При добавлении ко второй – 0.1232, 0.0893, 0.1566.

СПЛ в данном случаем определяется как максимальный коэф. наклона сигнала . Тогда для первого случая это 0.1268, для второго – 0.1566. Среднее значение 0.1417.

Рис.4 - при добавлении к первой координате

Рис.5 - при добавлении ко второй координате

Выводы: В данной лабораторной работе мы изучили два способа нахождения основной количественной характеристики странного аттрактора (СПЛ).

По нашему мнению, второй способ лучше, т.к. он даёт более точный и стабильный результат, в то время как первый способ нам дал отрицательный СПЛ, что противоречит определению хаотической системы. На рисунке 2 видно, что значения СПЛ сильно меняются на всём временном промежутке.

По второму способу СПЛ по среднему значению у нас равен 0.1417.

Приложение

1. Основной код

clear,clc;

a=0.95;

b=0.7;

c=0.6;

d=3.5;

e=0.25;

f=0.1;

syms x1 x2 x3;

dx=@(t,x)[(x(3)-b)*x(1)-d*x(2)...

;d*x(1)+(x(3)-b)*x(2)...

;c+a*x(3)-(x(3)^3)/3-(x(1)^2+x(2)^2)*(1+e*x(3))+f*x(3)*x(1)^3];

x0=0;

ddx=0.001;

% Второй метод

[t,y]=ode45(dx, [0 500], [-0.1387; -0.2527; 1.3259]);

plot(t,y)

% добавление дельты к первой координате

[t1,y1]=ode45(dx, [0 500], [-0.1387+ddx; -0.2527; 1.3259]);

t2=[0:0.02:500];

z=interp1(t,y,t2);

z2=interp1(t1,y1,t2);

% создание сетки

Del=[];

for i=1:length(t2)

nn=norm(z(i,:)-z2(i,:));

Del=[Del nn];

end

zt=log(Del/ddx);

plot(t2,zt);

hold on

% постраение аппроксимаций к графику, нахождение тангенса угла наклона

p1=polyfit(t2(1:2500),zt(1:2500),1);

yy1=polyval(p1,t2(1:2500));

plot(t2(1:2500),yy1);

o1=p1(1);

p2=polyfit(t2(4606:6173),zt(4606:6173),1);

yy2=polyval(p2,t2(4606:6173));

plot(t2(4606:6173),yy2);

o2=p2(1);

p3=polyfit(t2(20981:22179),zt(20981:22179),1);

yy3=polyval(p3,t2(20981:22179));

plot(t2(20981:22179),yy3);

o3=p3(1);

O1=[o1, o2, o3];

disp(O1)

O1=max([o1, o2, o3]);

hold off

% добавление дельты ко второй координате

[t3,y3]=ode45(dx, [0 500], [-0.1387; -0.2527+ddx; 1.3259]);

[t4,y4]=ode45(dx, [0 500], [-0.1387; -0.2527; 1.3259]);

t2=[0:0.02:500];

z3=interp1(t,y,t2);

z4=interp1(t3,y3,t2);

z5=interp1(t4,y4,t2);

Del=[];

for i=1:length(t2)

nn2=norm(z3(i,:)-z4(i,:));

Del=[Del nn2];

end

zt1=log(Del/ddx);

figure(2)

plot(t2,zt1);

hold on

% построение аппроксимаций к графику, нахождение тангенса угла наклона

tou=2485;

pp1=polyfit(t2(1:tou),zt1(1:tou),1);

yyy1=polyval(pp1,t2(1:tou));

plot(t2(1:tou),yyy1);

o11=pp1(1);

tou21=3513;

tou22=4640;

pp2=polyfit(t2(tou21:tou22),zt1(tou21:tou22),1);

yyy2=polyval(pp2,t2(tou21:tou22));

plot(t2(tou21:tou22),yyy2);

o22=pp2(1);

tou31=19186;

tou32=20422;

pp3=polyfit(t2(tou31:tou32),zt1(tou31:tou32),1);

yyy3=polyval(pp3,t2(tou31:tou32));

plot(t2(tou31:tou32),yyy3);

o33=pp3(1);

O2=[o11,o22, o33];

disp(O2)

O3=max([o11, o22, o33]);

hold off

% первый способ

Mas=[];

for i=1:1:tou

zch=z4(i,:);

A11=zch(3)-b;

A12=-d;

A13=zch(1);

A21=d;

A22=zch(3)-b;

A23=zch(2);

A31=-2*zch(1)-2*zch(1)*zch(3)*e+3*zch(1)^2*zch(3)*f;

A32=-2*zch(2)-2*zch(2)*zch(3)*e;

A33=a-zch(3)^2- (zch(1)^2)*e-e*zch(2)^2+f*zch(1)^3;

A=[A11, A12, A13;A21, A22, A23;A31, A32, A33];

Mas=[Mas max(real(eig(A)))];

end

figure(3)

plot(t2(1:tou),Mas)

2. Код проверки отрицательного СЧ.

Mas=[];

zch=z2(1867,:);

A11=zch(3)-b;

A12=-d;

A13=zch(1);

A21=d;

A22=zch(3)-b;

A23=zch(2);

A31=-(2*zch(1)+0)*(1+e*zch(3))+3*zch(1)^2*zch(3)*f;

A32=-(0+ 2*zch(2))*(1+e*zch(3));

A33=a-zch(3)^2-(zch(1)^2+ zch(2)^2)*(1+e)+f*zch(1)^3;

A=[A11, A12, A13;A21, A22, A23;A31, A32, A33];

Mas=[eig(A)];