лабораторные / 4l

МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

ОТЧЕТ по лабораторной работе №4

по дисциплине «МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ»

Тема: РЕАЛИЗАЦИЯ АЛГОРИТМОВ УПРАВЛЕНИЯ В СРЕДЕ MATLAB

Нуртазин И.

Попов М.М.

Преподаватель

Шпекторов А.Г.

С туденты гр. 6408 Лукьянцов К.В.

.

Санкт-Петербург

2020

Цель работы: Изучить основные принципы формирования алгоритмов управления, освоить средства моделирования систем управления в среде MATLAB.

Задача:

Синтезировать для объекта управления, который представляет собой пассажирский самолет Боинг-747, регулятор

обеспечивающий следующий спектр заданных собственных значений

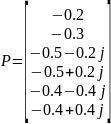
Замкнуть полученным регулятором объект и проверить корни характеристического полинома.

Изменить регулятор таким образом, чтобы время переходного процесса в замкнутой системе уменьшилось и сравнить коэффициенты нового и прежнего регулятора.

Исходная математическая модель:

Задание :

Объект управления – пассажирский самолет Боинг-747, который управляется в боковом движении с помощью руля направления и элеронов: их отклонения от нейтрального положения обозначены как _n и _e соответственно. В вектор состояния входят следующие компоненты: v_z – скорость бокового сноса; _y – угловая скорость по рысканию; _x – угловая скорость по крену;  – угол рыскания;  – угол крена; z – боковой снос. Система линейных дифференциальных уравнений, описывающих процесс стабилизации самолета в боковом движении при посадке, имеет следующий вид:

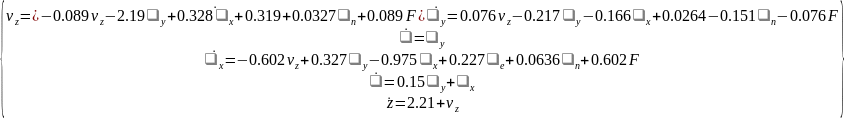
Регулятор:

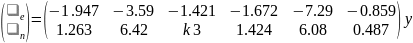
Содержание работы :

1. Сформировать SS-объект

Общий вид :

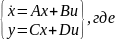
А – Матрица состояний, В – Матрица входов, С - Матрица выхода, D – Матрица обхода.

За переменные состояний возьмем следующий порядок:

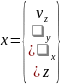
Выходами данного объекта будут следующими:

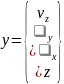
Входы данного объекта равны :

Матрицы А, В, С, D равны

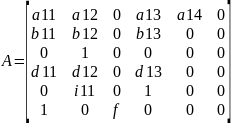
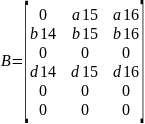
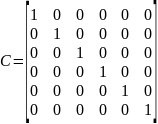
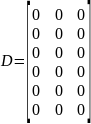
Где

a11=-0.089; a12=-2.19; a13=0.328; a14=0.319; a15=0.0327; a16=0.089; b11=0.076; b12=-0.217; b13=-0.166; b14=0.0264;

b15=-0.151; b16=-0.076; d11=-0.602; d12=0.327; d13=-0.975; d14=0.227; d15=0.0636; d16=0.602; i11=0.15; f=2.21;

Общие положения

К простейшему классу задач теории модального управления относится ситуация, когда выбором коэффициентов регулятора по состоянию можно обеспечить произвольное распределение корней характеристического полинома замкнутой системы.

Вместо системы введем в рассмотрение замкнутую систему, добавляя к уравнению объекта уравнение регулятора по состоянию

где K — постоянная матрица размера m n .

Получим модель замкнутой системы в виде

В рассматриваемой задаче матрицу K необходимо выбрать таким образом, чтобы матрица A  BK замкнутой системы имела заранее заданные собственные значения.

Ход работы:

1.

Задаем вектор собственных значений

Используем функцию place. Для этого используем матрицу В, включающую только первые два столбца, а также матрицу А и вектор Р .

2.

Замыкаем полученным регулятором объект с помощью функции lft с учетом операций, проведенных в предыдущей работе. Получаем систему, приведённую на рисунке.

Рис.1 Исследуемая система

Проверяем корни характеристического полинома.

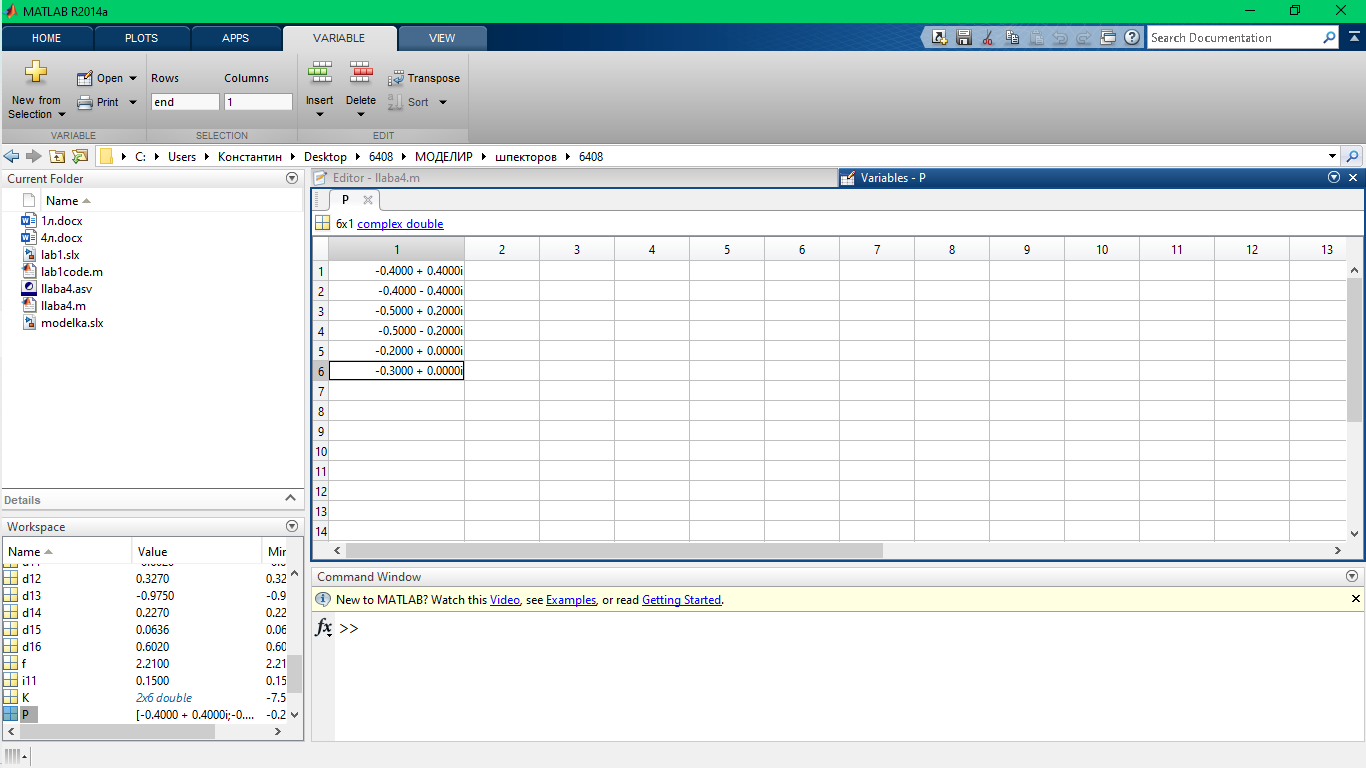
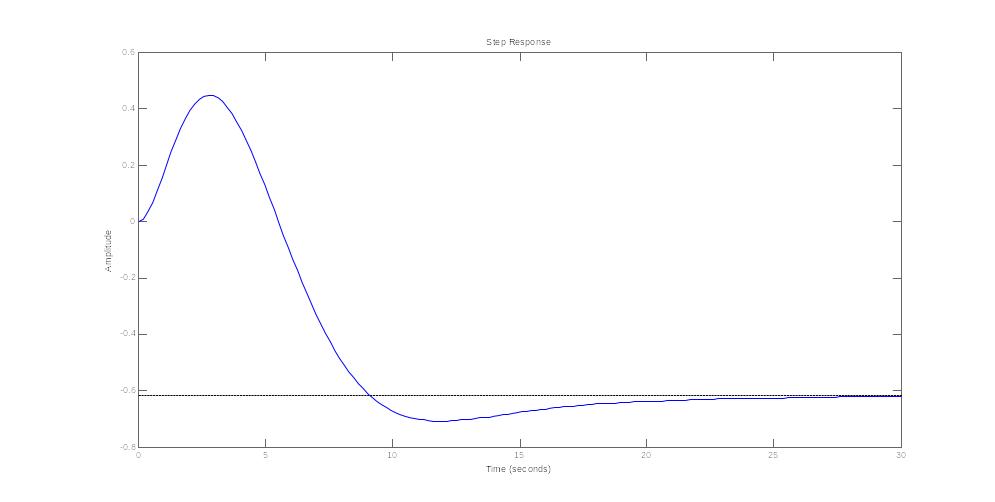
Рис.2 корни характеристического полинома и переходный процесс.

3.

Изменяем регулятор таким образом, чтобы время переходного процесса в замкнутой системе уменьшилось и сравниваем коэффициенты нового и прежнего регулятора.

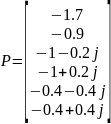
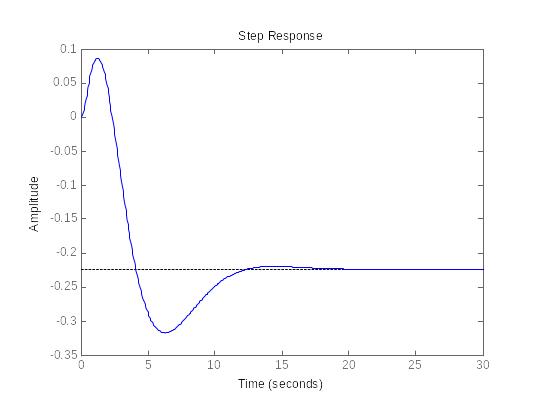
Рис.3 переходный процесс после изменения регулятора

Сравниваем коэффициенты регуляторов

Рис.4 Коэффициенты до изменения.

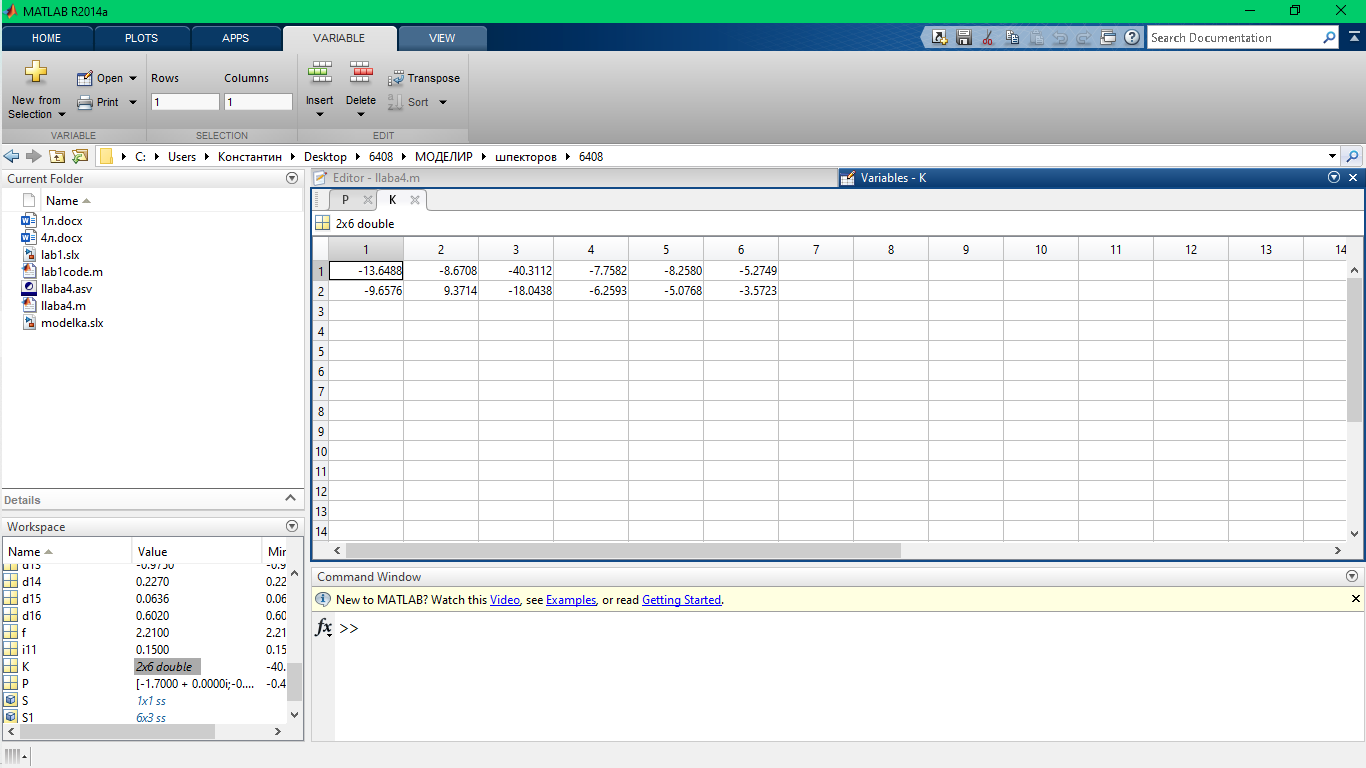
Рис.5 Коэффициенты после изменения.

Выводы: В ходе выполнения работы научились решать задачу теории модального управления простейшего класса. А именно получили желаемое распределение корней характеристического полинома замкнутой системы, путем изменения коэффициентов регулятора.

Скрипт:

clear,clc;

a11=-0.089;

a12=-2.19;

a13=0.328;

a14=0.319;

a15=0.0327;

a16=0.089;

b11=0.076;

b12=-0.217;

b13=-0.166;

b14=0.0264;

b15=-0.151;

b16=-0.076;

d11=-0.602;

d12=0.327;

d13=-0.975;

d14=0.227;

d15=0.0636;

d16=0.602;

i11=0.15;

f=2.21;

A=[a11, a12, 0, a13, a14, 0; b11, b12, 0, b13, 0, 0; 0, 1, 0, 0, 0, 0;...

d11, d12, 0, d13, 0, 0; 0, i11, 0, 1, 0, 0; 1, 0, f, 0, 0, 0];

B=[0, a15, a16; b14, b15, b16; 0, 0, 0; d14, d15, d16; 0, 0, 0; 0, 0, 0];

C=eye(6);

D=[0, 0, 0;0, 0, 0;0, 0, 0;0, 0, 0;0, 0, 0;0, 0, 0];

S1=ss(A,B,C,D);

P1=[-0.2;-0.3; -0.5-0.2j;-0.5+0.2j;-0.4-0.4j;-0.4+0.4j];

P2=[-1.7; -0.9; -1-0.2j; -1+0.2j; -0.4-0.4j; -0.4+0.4j];

B1=[B(:,1),B(:,2)];

K1=-place(A,B1,P1);

K2=-place(A,B1,P2);

set(S1,'B',[B(:,3),B(:,1),B(:,2)]);

S2=ss(K1);

S3=ss(K2);

S11=lft(S1,S2,2,6);

S22=lft(S1,S3,2,6);

set(S11,'C', [0, 0, 0, 0, 1, 0], 'D',[0]);

set(S22,'C', [0, 0, 0, 0, 1, 0], 'D',[0]);

P = pole(S22);

pzplot(tf(S22))

grid on

figure(1);

step(S11,30);

figure(2)

step(S22,30)

figure(3);

step(S11,30);

hold on

step(S22,30)

Практическая работа №3

Решить задачу параметрического синтеза для математической модели

подводного аппарата

где

ω – угловая скорость по дифференту,

ψ – дифферент,

δ – отклонение кормовых горизонтальных рулей,

u – управляющий сигнал на рули.

Уравнение регулятора имеет вид:

где

ψ_z = const – командная поправка по дифференту.

Все величины в приведенных уравнениях измеряются в градусах и градусах/с.

Значения коэффициентов объекта управления и автомата дифферента:

a11 = 0.1253, a12 = 0.004637 , b = 0.002198.

Командная поправка ψ_z определяется по формуле

с тем, чтобы замкнутая система имела наперёд заданное положение

равновесия по дифференту.

Скрипт:

clear,clc

a11=-0.1253;

a12=-0.004637;

b=-0.002198;

k1=-20;

k2=-1;

k3=-10;

Модель:

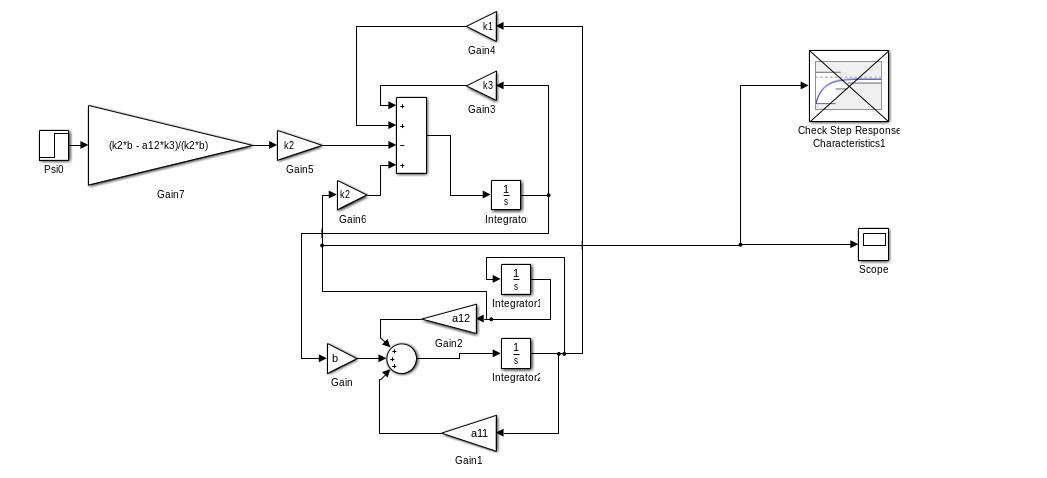
Результат:

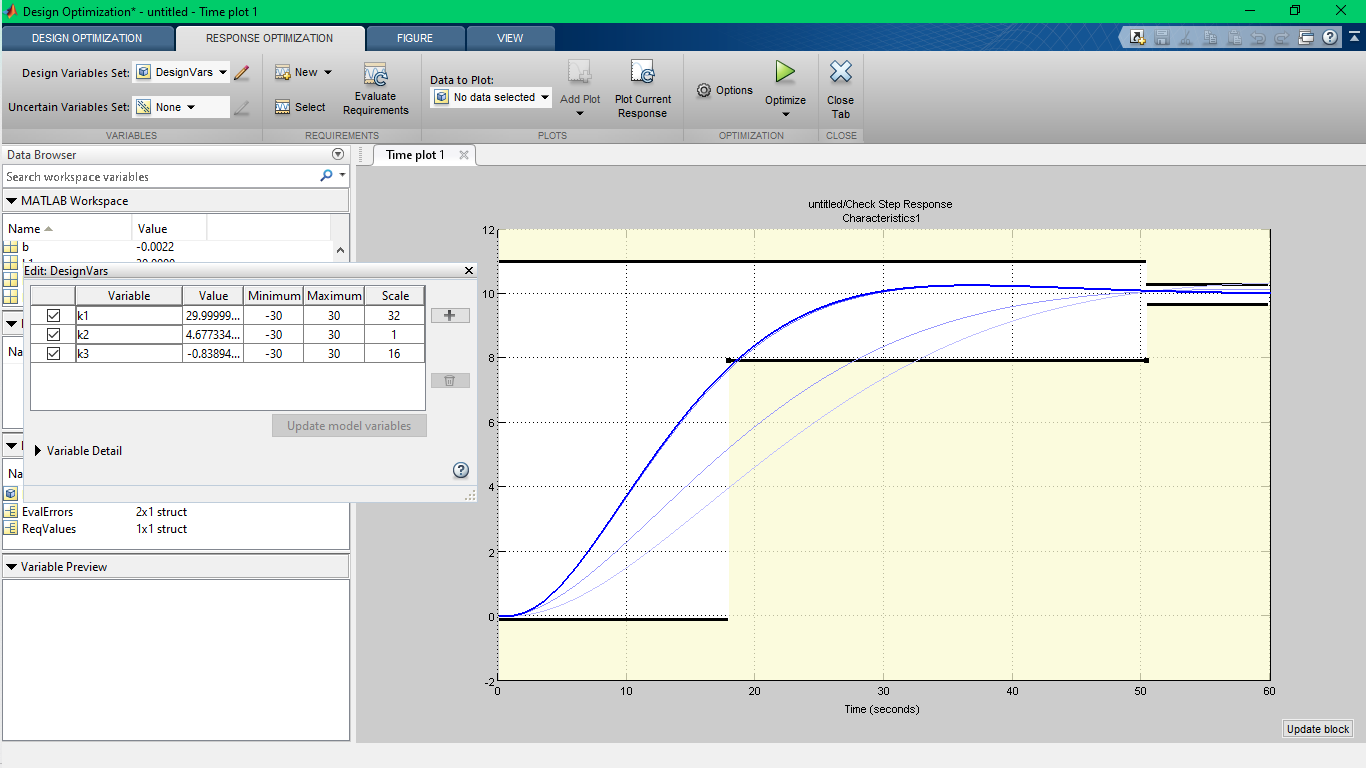
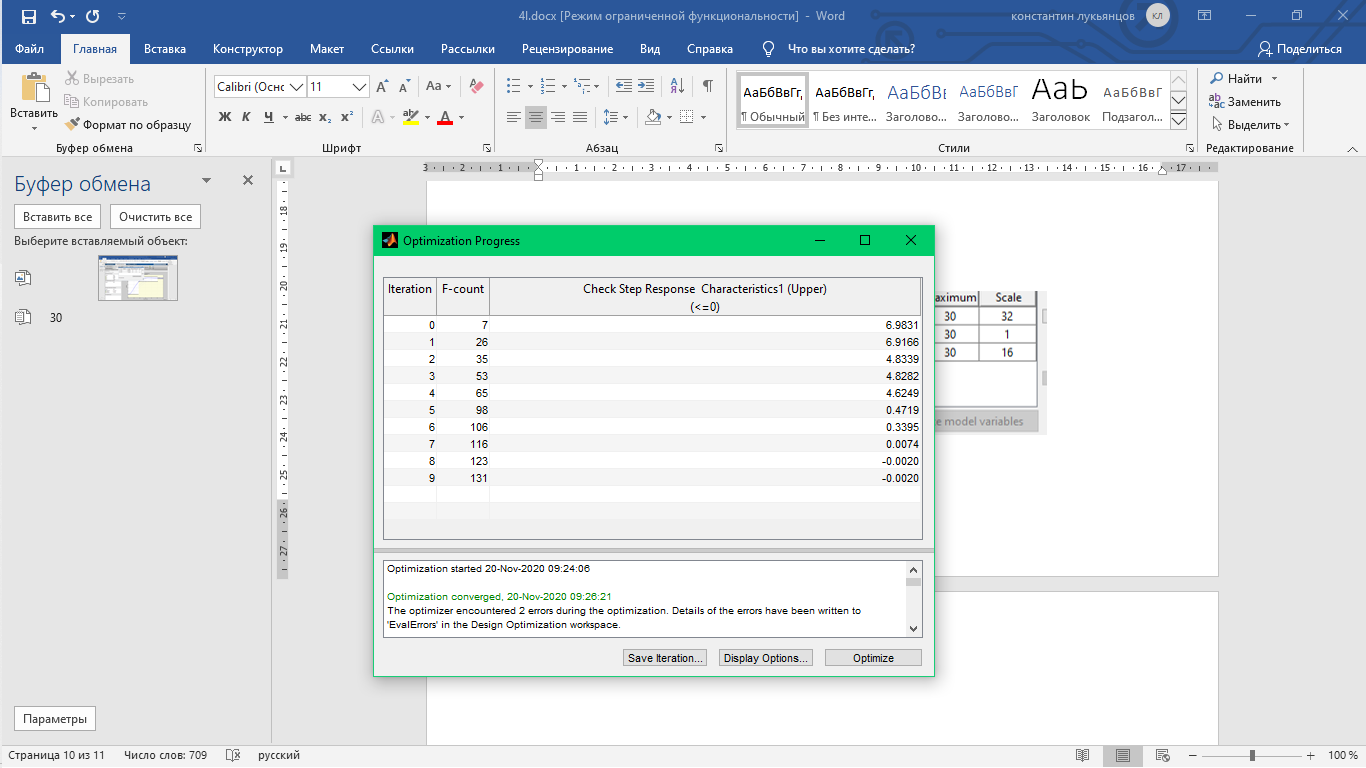
Полученные в процессе работы коэффициенты: