
Лекции / Т2_ДГМ
.pdf
средний квадрат ошибки системы. Если ввести в рассмотрение систему управления, построенную по принципу систем с обратной связью как показано на рисунке 2.4, где Fη –некоторое случайное возмущающее
воздействие, то ошибка управления может быть представлена как G B H
|
fη (t) |
u(t) |
y(t) |
|
W(p) |
|
-1 |
Рисунок 2.4
Так какFη – случайный процесс, то выходная переменная y(t), а следовательно и ошибка δ(t), будут также случайными процессами. Поэтому ошибку δ(t) характеризуют в статистическом плане. Наиболее простой статистической характеристикой является средний квадрат ошибки, который связан с дисперсией Iδ и мат. ожиданием Jδ следующим соотношением:
KL6B H 8 M I N JN
Таким образом, средний квадрат ошибки учитывает, как случайную составляющую ошибки ( Iδ ), так и систематическую (среднюю - Jδ ).
Действительно несложно показать, что
Iδ МL6δ Jδ8 M МOδ 2δJδ Jδ P МOδ P 2МLδMJδ
Jδ МOδ P Jδ , откуда |
М{δ }=Iδ Jδ . |
Положительный корень |
квадратный из среднего квадрата ошибки |
называется средней квадратичной ошибкой. Средняя квадратичная ошибка 16

имеет размерность выходного сигнала системы и поэтому при практических расчётах является более удобной характеристикой, чем средний квадрат ошибки. Критерий минимума средней квадратичной ошибки получил широкое распространение в практике проектирования систем управления электромеханическими объектами благодаря тому, что он прост в математическом отношении и для многих практических задач является удовлетворительной мерой успешности решения поставленной задачи управления:
η QIδ Jδ
Для астатических систем управления постоянная составляющая
ошибки управления равна нулю Jδ 0 . В этом случае
критерий минимума средней квадратичной ошибки получит вид:
η bIδ
Практика проектирования электромеханических систем управления показывает, что стремление минимизировать значение функционала η часто приводит к решению, которое не обеспечивает системе требуемого запаса устойчивости. Чтобы ограничить колебательность систем в этом случае, при решении задач на параметрическую оптимизацию, в качестве критерия качества целесообразно рассматривать составной критерий вида:
c c η, |
(2-15) |
в котором c и c -весовые коэффициенты, регулирующие вклад каждой составляющей функционала качества в его значение.
2.2 Организация вычисления составного критерия качества в процессе
параметрической оптимизации систем управления.
17
Ранее уже отмечалось, что критерий оптимальности должен быть сформирован таким образом, чтобы с одной стороны служить мерой качества управления, а с другой стороны его значение можно было сравнительно просто вычислить.
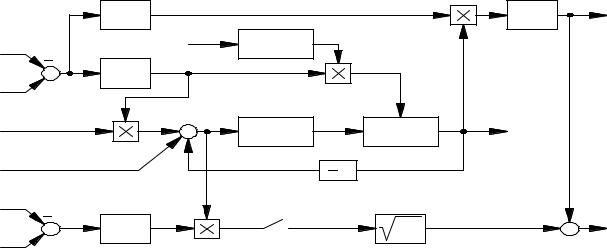
Применительно к виду критерия (2-15) рассмотрим возможную организацию его вычисления. С этой целью введём в рассмотрение структурную схему рисунок 2.5, где обозначено:
−W0 (p),Wр ( p) − передаточные функции неизменяемой части системы
(объекта управления) и регулятора, за счёт варьирования параметров
которого должен быть обеспечен экстремум критерия качества;
−Wф (p) − передаточная функция фильтра, который формирует из случайного процесса ψ (t) типа «белого шума» возмущающее воздействие Mη (t) с заданной спектральной характеристикой;
− |
t Т |
− |
текущее время с начала процесса моделирования; |
|||
− |
t1 |
− |
время окончания отработки системой ступенчатого управления |
|||
|
u(t) = uо и |
подачи |
на её вход |
синусоидального управляющего |
||
|
воздействия uв (t) = Um sin(ωэt) , а на объект управления возмущающего |
|||||
|
воздействия Mη (t); |
|
|
|||
− |
t2 |
− |
момент |
начала |
вычисления |
части Jη составного критерия |
качества;
−T0 − период дискретизации изучаемого процесса δ(t) , где δ(t) - текущее значение ошибки слежения за изменением управляющего воздействия.
18
f2
t1
f |
1 |
tT |
|
u B (t)
u 0 (t)
t2 |
|
|
t |
T |
f3 |
|
|
|
z |
2 |
|
|
|
|
|
F |
J 2 |
|
|
|
|
|
|
|
|
|||
|
U (t) |
|
|
U (t) |
|
|
|||
|
WФ |
( p) |
|
|
|
|
|||
z |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
δ (t) W |
( p) |
|
W |
( p ) |
y(t) |
|
|
|
|
|
|
|
|
|||||
|
|
Р |
|
|
Н |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
z3 |
|
δ (nTД |
) |
Sδ2 |
J |
1 |
J |
||
|
|
|
TД |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2.5 |
|
|
|
|
|||
Введенные в структурную схему функции f1 , f2 , f3 следующим образом определяют текущие значения переменных zi :
z1 = |
f1 (t1 |
,tT ) = |
|
|
tT |
≤ t1; |
|
0, |
|||||
|
1, |
tT |
> t1 . |
|||
|
|
|
|
|||
z2 = |
f2 (t1 |
,tT ) = |
|
|
tT |
≤ t1; |
|
1, |
|||||
|
0, |
tT |
> t1 . |
|||
|
|
|
|
|||
z3 = |
f3 (t2 |
,tT ) = |
|
tT |
≤ t2 ; |
|
|
0, |
|||||
|
1, |
tT |
> t2 . |
|||
|
|
|
|
|||
Организация процесса моделирования проектируемой системы для вычисления функционала качества J на i-ом шаге движения к экстремуму (минимуму) поясняет рисунок 2.6, на котором обозначено: yM , yУ - максимальное и установившееся значения выходной переменной на интервале 0 ≤ tT < t1 . Весь процесс моделирования условно может быть разделен на 2 этапа.
На первом этапе ( 0 ≤ tT < t1 ) на вход системы подается ступенчатое управляющее воздействие u0 (t) и определяется значение
J2 |
= F(y,α,m) = |
|
α ≤ 45% |
& m ≤ 5; |
|
0, |
|||||
1000, |
α > 45% |
|| m > 5, |
|||
|
|
||||
|
|
|
|
|
19
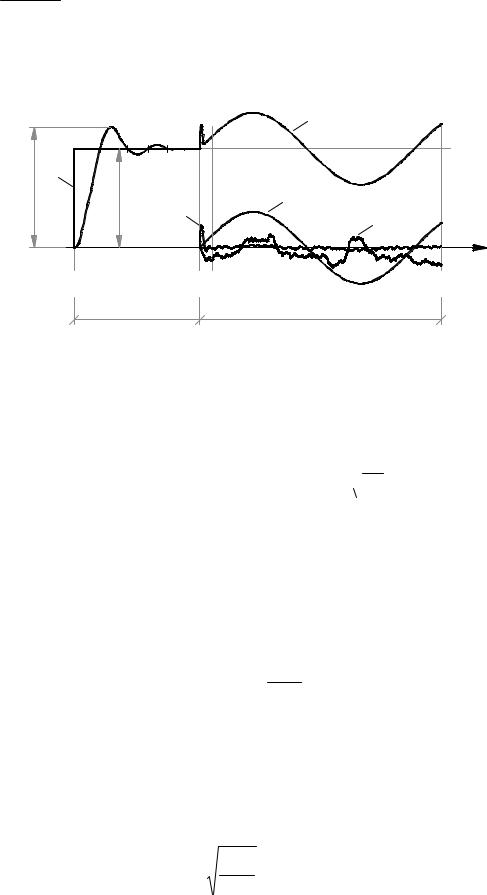
где α = yM − yУ 100% - величина перерегулирования, а m – число переходов |
||||||
yУ |
|
|
|
|
|
|
кривой переходного процесса выходной переменной y через установившееся |
||||||
значение при отработке системой ступенчатого управления. |
|
|||||
|
|
|
|
|
y(t) |
|
|
m = 1 |
2 |
3 |
4 |
|
|
yM |
u0 (t) |
|
|
|
|
|
y |
δ(t) |
uB (t) |
|
|||
|
|
|||||
|
|
У |
U (t) |
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
tT |
|
0 |
|
|
|
t1 t2 |
tK |
|
|
1 этап |
|
2 этап |
|
|
Рисунок 2.6
На втором этапе (t1 < tT ≤ tK ) на вход системы подается эквивалентное гармоническое воздействие, а на объект управления – возмущение Uµ (t) с заданной спектральной характеристикой. Начиная с момента t2 , вычисляется оценка средней квадратической ошибки наведения 
 Sδ2 .
Sδ2 .
Время tB = tK − t2 , необходимое для вычисления оценки дисперсии ошибки наведения Sδ2 , может быть определено из следующих соображений.
Известно, что дисперсия оценки дисперсии может быть представлена в виде [1]:
Var[Sδ2 ] = 2σδ4 ,
n −1
где σδ2 - истинное значение дисперсии ошибки, а n – число наблюдений. Зададимся вероятностью того, что интервальная оценка дисперсии должна накрывать ее истинное значение величиной равной Р=0.95, что соответствует 2σ -пределу. Тогда можно записать
22σδ4 = ∆n , n −1
20

где ∆n - ширина интервала, который с вероятностью Р=0.95 будет накрывать истинное значение дисперсии.
Если ∆n принять равной, например, 10% от истинного значения, то
|
∆n |
|
|
|
|
|
|
|
|
|
= |
∆n |
|
|
|
|
есть положить |
= 0.1 , тогда |
|
2 2 |
|
|
= 0.1 , |
откуда |
требуемое |
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
σ 2 |
|
|
|
|
|
|
n −1 |
σ 2 |
|
|
|
||||
количество наблюдений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
n = |
|
|
|
|
|
+1 ≈ 800. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь для |
определения значения tB |
необходимо |
оценить |
величину |
||||||||||||
периода дискретизации TД изучаемого процесса. Обычно это может быть сделано на основании анализа характеристик внешних воздействий, приложенных к системе. Например, если в результате такого анализа принято
решение, что детализация наблюдений с частотами выше |
f =10Гц не будет |
||||||||
приводить к повышению информативности изучаемого |
процесса, тогда |
||||||||
T |
|
|
1 |
= 0.05c , а, следовательно, t |
|
=T |
|
n = 0.05 800 = 40c. |
|
Д |
|
B |
Д |
||||||
|
|
2 f |
|
|
|
||||
|
|
|
|
|
|
|
|
||
21
