
Лекции / Т2_ДГМ
.pdfТЕМА 2. ФОРМИРОВАНИЕ КРИТЕРИЕВ ОПТИМАЛЬНОСТИ ПРИ РАЗРАБОТКЕ И ИССЛЕДОВАНИИ СИСТЕМ УПРАВЛЕНИЯ ЭЛЕКТРОМЕХАНИЧЕСКИМИ ОБЪЕКТАМИ
Основное назначение любого критерия оптимальности системы управления состоит в том, чтобы численно оценить качество проектируемой системы и степень успешности решения требуемых задач управления. Выбор статистических критериев качества СУ, также как и детерминированных, не может быть формализован в рамках математической теории. Однако, к любому критерию оптимальности предъявляются два общих требования:
1.Служить мерой успешности решения поставленной задачи управления;
2.Должен быть достаточно просто, чтобы можно было решить задачу определения оптимальной системы (вычисления
выбранного критерия оптимальности).
Учитывая специфику систем управления электромеханическими объектами, практически часто критерий оптимальности формируются их двух частей.
Одна из этих частей является мерой соответствия переходной характеристики проектируемой системы наперед заданной при отработке типовых управляющих воздействий. Эта часть критерия качества является детерминированной. Другая часть составного критерия является мерой успешности управления при действии на систему случайных возмущений (например, момента нагрузки, обусловленного ветровым потоком). Следовательно, вторая часть критерия качества является случайной величиной, и для ее оценки могут быть использованы числовые характеристики (среднее значение, дисперсия, среднее квадратическое отклонение).
6
Таким образом, в общем случае критерий качества формируется из двух частей
J = Jv + Jη .
Рассмотрим практически часто применимые оценки успешности управления для обеих частей составного критерия качества.
2.1 Формирование детерминированной части составного критерия
качества
В качестве меры соответствия переходной характеристики проектируемой системы наперед заданной, широкое распространение получили интегральные критерии квадратичных форм вида:
t |
2 |
&2 |
+γ |
&&2 |
&&&2 |
t |
(2-1) |
Jν =∫ |
(x |
+γ1x |
2x |
+γ3x |
+...)dt=∫Vdt, |
||
0 |
|
|
|
|
|
0 |
|
где x-выходная переменная, движение которой анализируется при переводе системы из некоторого установившегося состояния в нулевое, γi - весовые коэффициенты при квадратах производных i-ого порядка от выходной координаты, t - время перехода СУ из одного установившееся состояния в другое.
Известно, что экстремалью для функционала (2-1) является одно из решений однородного дифференциального уравнения Эйлера-Пуассона:
∂V |
− |
d ∂V |
+ |
d 2 |
∂V |
− |
d3 |
∂V |
+ ...... = 0 |
, |
||
∂x |
|
& |
2 |
&& |
3 |
&&& |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||
|
dt ∂x |
|
dt ∂x |
|
dt ∂x |
|
|
|||||
в котором число членов соответствует количеству слагаемых квадратичной формы V. Под экстремалью в данном случае понимается решения такого дифференциального уравнения, которое доставляет минимальное значение выбранному функционалу. Если ограничиться первыми четырьмя членами
7
квадратичной формы под знаком интеграла в выражении (2-1) и принять во
внимание, что
∂V |
= 2x; |
d ∂V |
&& |
, |
d ∂V |
= 2γ 2x |
(4) |
|
d ∂V |
= 2γ3x |
(6) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
∂x |
& |
= 2γ1x |
&& |
|
, |
&&& |
|
, |
|||||||
|
dt ∂x |
|
|
dt ∂x |
|
|
|
dt ∂x |
|
|
|
||||
то соответствующее ему уравнение Эйлера-Пуассона в операторной форме записи можно представить как:
1 0 |
(2-2) |
Решение этого уравнения имеют 3 корня с отрицательной вещественной частью, а три с положительной. Практический интерес представляют устойчивые системы, поэтому в решении уравнения (2-2) следует учитывать корни только с отрицательной вещественной частью.
Таким образом, экстремалью для выбранного функционала
|
|
γ γ γ |
(2-3) |
|
|
|
|
|
|
будет решение дифференциального уравнения третьего порядка, корни которого соответствуют корням уравнения Эйлера – Пуассона с отрицательной вещественной частью:
Отмеченный результат позволяет формировать расчет весовых коэффициентов функционала по желаемому виду движения выходной координаты, заданному однородным дифференциальным уравнением .
2.1.1 Методика формализованного выбора весовых коэффициентов в
составе интегральных критериев от квадратичных форм.
Пусть желаемое движение некоторой выходной переменной « в»
определяется переходной функцией:
в |
|
|
√ · |
|
· sin·* $ |
· , |
|
|||
|
|
!·#$ |
|
|
|
&·#$ |
|
√ |
|
(2 - 4) |
|
|
|
|
|
|
|
||||
8
которое при начальных условиях: в 0 1; в 0 в 0 0
является решением характеристического уравнения системы, настроенной на симметричный оптимум:
8-. 8-. 4-. 1 0 (2 - 5),
где Tm-эквивалентная малая постоянная времени, характеризующая быстродействие системы.
Чтобы решение (2-5) являлось экстремалью для функционала (2-3) ,
его весовые коэффициенты γ0 должны выбираться следующим образом:
1.Составляется дифференциальное уравнение аналогичное (2-5), но для корней расположенных в правой полуплоскости комплексной переменной p:
8-. 8-. 4-. 1 0 |
(2-6) |
2.Формируется уравнение, соответствующее уравнению Эйлера – Пуассона, путём перемножения уравнений (2-5) и (2-6):
64-. 64-. 64-. 16-. 16-. 1 0 (2-7)
3.Определяются весовые коэффициенты γ0 , путём приравнивания коэффициентов этого уравнения и уравнения Эйлера-Пуассона при одинаковых степенях оператора p. Указанные действия приводят к результату:
γ 64- . ; γ 0; γ 0
Таким образом, решение дифференциального уравнения (2-5) является
экстремалью для функционала:
|
в 64-. в |
(2-8) |
|
|
|
9
Минимизация этого функционала в процессе параметрической оптимизации системы обеспечит, если это возможно, выходной переменной « в » движение в соответствии с переходной характеристикой (2-4). Следовательно, одно из существенных достоинств критериев качества (2-1) состоит в возможности формализованного выбора таких весовых коэффициентов γ0 квадратичной формы V, при которых устанавливается соответствие между желаемым переходным процессом в проектируемой системе управления, заданным решением однородного дифференциального уравнения, и функционалом качества, подлежащим минимизации.
Пример применение изложенной методики для выбора весовых коэффициентов функционала вида
|
|
2 |
γ γ 3 2 4 |
|
|
с целью обеспечения проектируемой системе наперед заданной переходной характеристики.
Пусть желаемое движение выходной переменной проектируемой системы при отработке входного ступенчатого управления задаётся решением однородного дифференциального уравнения соответствующего стандартной форме Бинома второго порядка
H( p) = (p + ω |
)2 = p2 + 2ω |
0 |
p + ω2 |
= 0 |
(2-9), |
0 |
|
0 |
|
|
где ω0 - параметр определяющий время переходного процесса. Чем больше
ω0 , тем при прочих равных условиях меньше время переходного процесса.
Требуется определить весовые коэффициенты функционала
t |
|
2 |
|
|
2 |
|
&&2 |
t |
Jv2 = ∫ |
(x |
+ γ |
& |
+ γ |
)dt = ∫V2dt, |
|||
|
1x |
|
2 x |
|||||
0 |
|
|
|
|
|
|
|
0 |
10
при которых решение уравнения (2-9) будет экстремалью для функционала
Jv2 .
Для определения коэффициентов γ i целесообразно действовать в следующем порядке:
1.Составить операторное уравнение Эйлера-Пуассона, соответствующее виду «V2»:
∂V |
− |
d ∂V |
+ |
d2 |
|
∂V |
= 0 |
|
→ |
2x − 2γ |
|
&x& + 2γ |
|
x(4) |
= 0 , откуда |
|||||
2 |
|
|
2 |
|
|
|
|
2 |
|
1 |
2 |
|||||||||
∂x |
& |
2 |
|
|
&& |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dt ∂x |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
γ |
2 |
p4 |
− γ |
1 |
p2 |
+1+ 0 |
|
(2-10) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.Составить уравнение, аналогичное (2-9), но для корней расположенных в правой полуплоскости комплексной переменной.
Если уравнение (2-9) имеет корни в левой полуплоскости: p1,2 = −ω0 ,то
искомое уравнение может быть получено как :
(p − ω |
)( p |
− ω |
) = p2 − 2ω |
0 |
p + ω2 |
(2-11) |
0 |
|
0 |
|
|
|
3.Составить уравнение, соответствующее уравнению Эйлера Пуассона (2-10) в операторной форме, путём перемножения уравнений (2-9), (2- 11) друг на друга
(p2 + 2ω0 p + ω02 ) ( p2 − 2ω0 p + ω2 ) = p4 − 2ω02 p2 + ω04 = 0
или после несложных преобразований |
|
||||
1 |
p4 − |
2 |
p2 +1= 0 |
(2-12) |
|
|
ω4 |
ω2 |
|||
|
|
|
|
||
0 |
|
0 |
|
|
|
4. Определить коэффициенты «γ i » путём приравнивания коэффициентов уравнения Эйлера_ Пуассона и соответствующего ему уравнения (2-
12) |
|
|
при |
|
одинаковых степенях оператора «p». В нашем примере: |
||||||
γ |
|
= |
|
1 |
;γ |
|
= |
|
2 |
. Таким образом, решение уравнения (2-9)_ будет |
|
2 |
ω4 |
1 |
ω2 |
||||||||
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
0 |
|
|||
экстремалью для функционала
11
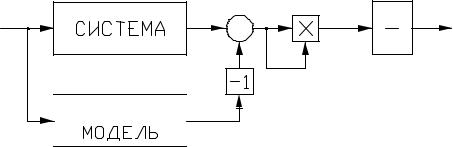
t |
|
2 |
+ γ |
|
2 |
+ γ |
&&2 |
|
Jv2 = ∫ |
(x |
& |
)dt . |
|||||
|
1x |
|
2x |
|||||
0 |
|
|
|
|
|
|
|
|
2.1.2 Формирование критериев качества при решении
детерминированных задач на параметрическую оптимизацию систем
управления с использованием эталонных моделей.
Другой практически часто применяемый подход к формированию функционала качества проектируемой системы при необходимости обеспечить ей наперёд заданную переходную характеристику основан на применении эталонных моделей. В этом случае, как показано на схеме рисунке 2.1, в процессе оптимизации на входы обеих систем подаётся
uу |
xв |
ε |
ε2 |
1 |
Jvэ |
|
|
|
|
p |
|

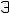





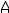

 xэ
xэ
Рисунок 2.1
ступенчатое входное воздействие, а функционал качества формируется как
э |
6в э 8 , |
(2-13) |
|
9 |
|
где в, э – выходные переменные проектируемой системы и эталонной модели, t – интервал времени, за который проектируемая система переходит из одного устойчивого состояния в другое. Желая обеспечить выходной переменной в движение, аналогично э , необходимо так подобрать варьируемые параметры проектируемой системы, чтобы э→ 0. Введение «ЭМ» для организации процедуры параметрической оптимизации СУ имеет свои достоинства и недостатки. Положительным моментом можно считать
12
отсутствие производных от выходной переменной в (2-13), что упрощает математическое выражение функционала качества и процедуру его вычисления. К недостаткам следует отнести необходимость реализации самой модели. Поэтому на практике стремятся задавать эталонное движение моделями сравнительно невысоких порядков.
Достаточно часто такие модели реализуют с использованием принципов модального управления, т.е. желания разместить корни характеристического уравнения замкнутой системы в соответствие с наперёд заданной стандартной формой.
Существуют различные подходы к выбору желаемых корней характеристического уравнения замкнутой системы. Если все корни выбираются одинаковыми, причем действительными и отрицательными со значением модуля равным ω0 , то характеристическое уравнение порядка n обращается в бином Ньютона
: ; 9 < |
(2-14) |
Стандартные формы, соответствующие (2-14) получили название биномиальных. Их вид для ряда значения «n» можно представить
следующим образом: |
|
H(p) =1 ;9 |
n=1; |
1 2;9 1;9 |
n=2; |
1 3;9 3;9 1;9 n=3;
1 4;9 6;9 4;9 1;9 n=4 и т.д.
Другим широко распределённым распределением корней, является распределение Баттерворта. В этом случае корни располагаются на полуокружности радиуса ω0 в левой полуплоскости комплексной переменной
13

«p». Угол между мнимой осью и лучом, проходящим через ближайший к ней корень и начало координат равен половине угла между соседними корнями.
Стандартная форма Баттерворта для ряда значений «n» имеет вид:
H(p) = 1 ;9 |
n=1; |
1 1,4;9 1;9 |
n=2; |
1 2;9 2;9 1;9 n=3;
1 2,6;9 3,4;9 2,6;9 1;9 n=4.
Если считать, что передаточная функция проектируемой системы (модели) по управлению имеет вид:
|
( p) = |
∆x ( p) |
= |
ωn |
|
W |
в |
0 |
, |
||
|
|
||||
у |
|
∆u( p) |
|
H( p) |
|
|
|
|
|||
то есть её динамические свойства полностью определяются видом характеристического уравнения, и ввести в рассмотрение нормированное время ? ; 9 , то реакция систем спроектированных в соответствии с названными стандартными формами на единичное ступенчатое воздействие может быть представлена переходными характеристиками, показанными на рисунке 2.2.
x |
|
|
|
x |
|
n= 2 |
3 |
4 |
1,0 |
n= 2 |
|
|
1,0 |
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
0,5 |
|
|
|
0,5 |
|
|
|
|
|
|
|
|
ω0t |
|
|
|
ω0t |
0 |
Форма |
5 |
10 |
0 |
Форма 5 |
10 |
||
|
Биноминальная |
|
|
Баттерворта |
||||
|
|
|
|
Рисунок 2.2 |
|
|
||
14

Если при разработке системы стремиться обеспечить реакцию на ступенчатое воздействие в соответствие со стандартной формой Баттерворта, то эталонная модель может быть выполнена в соответствие с передаточной функцией:
@эм |
∆э |
;9 |
CD |
|
∆B |
2;9 2;9 ;9 |
|||
|
|
Структурная схема такой модели показана на рисунке 2.3
u(p) -αp |
ωо |
ωо |
ω |
xэ(p) |
|
e |
|
p |
2 |
о |
|
2p |
p |
|
|
||
|
|
|
|||
|
|
|
-1 |
|
|
|
|
-1 |
|
|
|
|
-1 |
|
|
|
|
Рисунок 2.3
Звено чистого запаздывания" CD" введено на вход эталонной модели 3-го порядка с целью имитации движений, соответствующих стандартным формам Баттерворта более высоких порядков. Обязательным условием успешной реализации поиска экстремума функционала (2-13) является необходимость обеспечения одинаковых статических коэффициентов передачи проектируемой системы и эталонной модели на каждом шаге движения к экстремуму. В противном случае условия решения задачи становится некорректным.
2.2 Формирование стохастической части составного критерия качества
Наиболее простым и часто употребляемым критерием оптимальности
системы по точности, при действии на неё случайных возмущений, является
15
