Лекции / Т1_ДГМ

ТЕМА 1 МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ

1.1Постановка задачи оптимизации

Для того чтобы применять математические результаты и численные

методы теории оптимизации для решения конкретных инженерных задач, необходимо выполнить определенный объём подготовительной работы, включающей в себя:

−Определение границ системы;

−Построение адекватной модели системы;

−Определение проектных параметров;

−Выбор целевой функции.

Перечисленная последовательность действий составляет содержание процесса постановки задачи инженерной оптимизации. Корректная постановка задачи служит ключом к успеху оптимизационного исследования и ассоциируется в большей степени с искусством, нежели с точной наукой.

Определение границ системы. Границы системы задаются пределами, отделяющими систему от внешней среды и служат для выделения системы из её окружения. При проведении анализа обычно предполагается, что взаимосвязи между системой и внешней средой зафиксированы на некотором выбранном уровне представления. Тем не менее, поскольку таких взаимосвязей реально всегда существует больше, чем предполагается, определение границ системы является первым шагом в процессе приближённого описания реальной системы.

В ряде случаев может оказаться, что первоначальный выбор границы является слишком упрощенным. Для более точного описания данной инженерной системы может возникнуть необходимость расширения установленных границ системы путём включения в описание других подсистем, оказывающих существенное влияние на функционирование исследуемой системы.

1

Разумеется, расширение границ системы повышает размерность описания и в значительной мере затрудняет её анализ. Очевидно, что в инженерной практике следует, насколько это возможно, стремиться к разбиению больших сложных систем на относительно небольшие подсистемы, которые можно исследовать по отдельности. Однако, при этом необходимо убедится, что такая декомпозиция существенно не изменяет поведение реальной системы.

Проектные параметры. Этот термин обозначает независимые переменные параметры, изменяя значения которых можно влиять на качество работы проектируемой системы. При выборе независимых переменных целесообразно руководствоваться правилом, согласно которому следует рассматривать только те переменные, которые оказывают существенное влияние на критерий качества, выбранный для оценки успешности работы системы. Обычно, число проектных параметров обозначают через «n», а сами проектные параметры через «x». Таким образом, n проектных параметров данной задачи будем обозначать как

x1, x2, x3, ……., xn.

Целевая функция. Целевая функция это конкретный критерий, на основе которого можно оценить характеристики системы, с тем чтобы определить наилучшие. Вариантов возможных формулировок таких критериев строго говоря бесконечное множество. При их формулировке могут использоваться как технические (точность слежения, точность стабилизации), так и технологические факторы (минимум энергетических затрат, чистая прибыль).

С математической точки зрения целевая функция описывает некоторую (n+1)- мерную поверхность. Её значение определяется проектными параметрами:

J = F(x1,x2 ,..., xn )

Если имеется только один проектный параметр, то целевая функция

может быть представлена кривой на плоскости

2

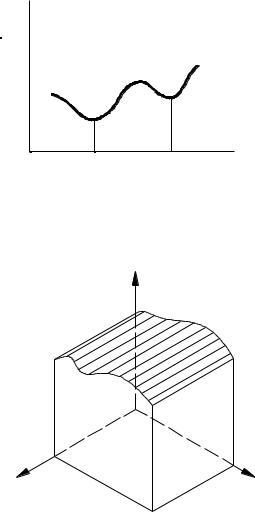
F(x1)

одномерная целевая функция

min

x1

Если проектных параметров два, то целевая функция будет изображаться поверхностью в пространстве трёх измерений.

F(x1,x2)

В ряде задач оптимизации требуется введение более одной целевой функции. Иногда одна из них оказывается несовместимой с другой. Примером такой задачи может служить проектирование самолётов, когда одновременно требуется обеспечить максимальную прочность, минимальный вес и минимальную стоимость. В таких случаях вводят систему приоритетов и ставят в соответствие каждой отдельной целевой функции некоторый безразмерный множитель (весовой коэффициент). В результате появляется функция компромисса, позволяющая в процессе оптимизации пользоваться составной целевой функцией:

J = J0 + ρ1J1 + ρ2 J2 ,

где ρi - весовые коэффициенты.

3

Одни алгоритмы оптимизации приспособлены для поиска максимума, другие для поиска минимума. Однако, независимо от типа решаемой задачи на экстремум, можно пользоваться одним и тем же алгоритмом, так как задачу оптимизации на минимум можно легко преобразовать в задачу на поиск максимума, поменяв знак целевой функции на обратный.

F(x)

min F(x)

max-F(x)

Пространство параметров не столь велико, как может показаться, поскольку оно обычно ограничено рядом условий, связанных с физической сущностью задачи. Ограничения могут быть столь сильными, что задача не будет иметь не одного удовлетворительного решения. Ограничения делятся на две группы: ограничения-равенства и ограничения-неравенства.

Ограничения-равенства – это зависимость между проектными параметрами, которая должна учитываться при отыскании решения. Они отражают законы природы, экономики, господствующего вкуса и наличие необходимых материалов. Число ограничений равенств может быть любым. Они имеют вид

Ci (x1,x2 ,...xn ) = 0 , i =1,...,k

Если какое либо из этих соотношений можно разрешить относительно одного из проектных параметров, то это позволяет исключить данный параметр из процесса оптимизации. Тем самым уменьшается число измерений пространства проектирования и упрощается решение задачи.

4

Ограничений-неравенств, как и ограничений равенств может быть

сколько угодно, причём все они могут быть представлены в виде:

H j (x1,x2 ,...xn ) ≤ 0.

Следует отметить, что очень часто в связи с ограничениями оптимальное значение целевой функции достигается не там, где её поверхность имеет нулевой градиент. Нередко лучшее решение соответствует одной из границ области проектирования.

Продемонстрировать постановку задачи оптимизации лучше всего на конкретном примере.

1.2 Пример решения задачи оптимизации

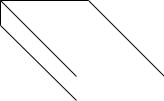
Пусть требуется спроектировать прямоугольный контейнер объёмом 1 м3. Желательно, чтобы на изготовление таких контейнеров затрачивалось как можно меньше материала (при условии постоянства толщины стенок это означает, что площадь поверхности должна быть минимальной), так как при этом он будет дешевле. Чтобы контейнер удобно было брать автопогрузчиком, его ширина должна быть не менее 1,5 м.

Ограничение – неравенство: x1 ≥ 1,5 м.

Ограничение – равенство благодаря своей простоте позволяет уменьшить размерность задачи. Действительно, если x3 =1/x1x2, то x3 можно исключить из проектных параметров.

Формулируя вновь задачу, имеем: Проектные параметры: x1, x2. Ограничение –равенство: нет

5

После того, как задача сформулирована стандартным способом, её

можно решать любым численным методом. Можно воспользоваться стандартным определением минимума и принять, что:

∂SП = ∂SП = 0 ∂x1 ∂x2

Тогда, с учётом определения Sп, получим два уравнения:

Однако, при таком решении не удовлетворено ограничениенеравенство и, следовательно, оно неприемлемо.

Задачи оптимизации можно классифицировать в соответствии с видом функций F,Ci ,Hj и размерностью вектора x.

Задачи без ограничений, в которых x представляет собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но вместе с тем весьма важный подкласс оптимизационных задач.

Задачи, которые содержат только линейные функции вектора непрерывных переменных x, называются задачами линейного программирования.

Задачи с нелинейными F,C ,H принято называть задачами нелинейного программирования. Если F(x) - квадратичная функция, то мы имеем дело с задачами квадратичного программирования.

6