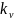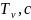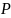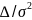Лабораторные / ДГМ_1_20в_6408_НуртазинИ

МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра РАПС

ОТЧЕТ

по практической работе №1

по дисциплине «Дополнительные главы математики»

Тема: Формирование случайных сигналов с заданными вероятностными характеристиками

Вариант 20

Студент гр. 6408 ____________________ Нуртазин И.

Преподаватель ____________________ Туркин Д.Н.

Санкт-Петербург

2021

Цель работы: Сформировать случайный процесс с требуемыми вероятностными характеристиками в среде Simulink.

В работе требуется инструментальными средствами Simulink сформировать случайный процесс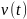 , имеющий наперёд заданные плотности вида:

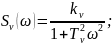
Исходные данные берутся из таблицы 1.1 (вариант 20):

№ варианта
20	1.1	5.5	0.95	0.1

Где 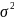– истинное значение дисперсии;

и 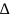– значения уровней вероятности.

– заданный коэффициент передачи;

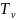– заданная постоянная времени;

Для оценки среднего и дисперсии по выборке конечной длины использовать следующие выражения:

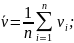
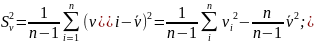
Расчётным путём необходимо получить дисперсию по формуле:

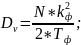
Где 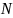– уровень интенсивности генератора белого шума;

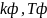– соответственно коэффициент передачи и постоянная времени формирующего фильтра.

Ход работы:

Рассчитаем коэффициент передаци формирующего фильтра:

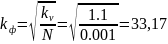
Уровень спектральной плоскости по условию принят равным

Постоянная времени:

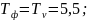
Эти данные необходимо подставить в уравнение:

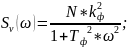
Требуемое число наблюдений получим из уравнения:

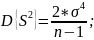
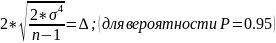
Отсюда получим:

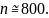
Период дискретизации экспериметальных точек:

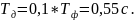
Отсюда модельное время .

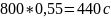Рассчитаем дисперсию по формуле:

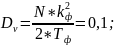
Для моделирования необходимо реализовать модель, состоящую из генератора белого шума, фильтра первого порядка с параметрами, обеспечивающими требуемый уровень спектральной плотности на его выходи, и устройства для оценки значений среднего и дисперсии формируемого сигнала. Полная схема изображена на рисунке 1.

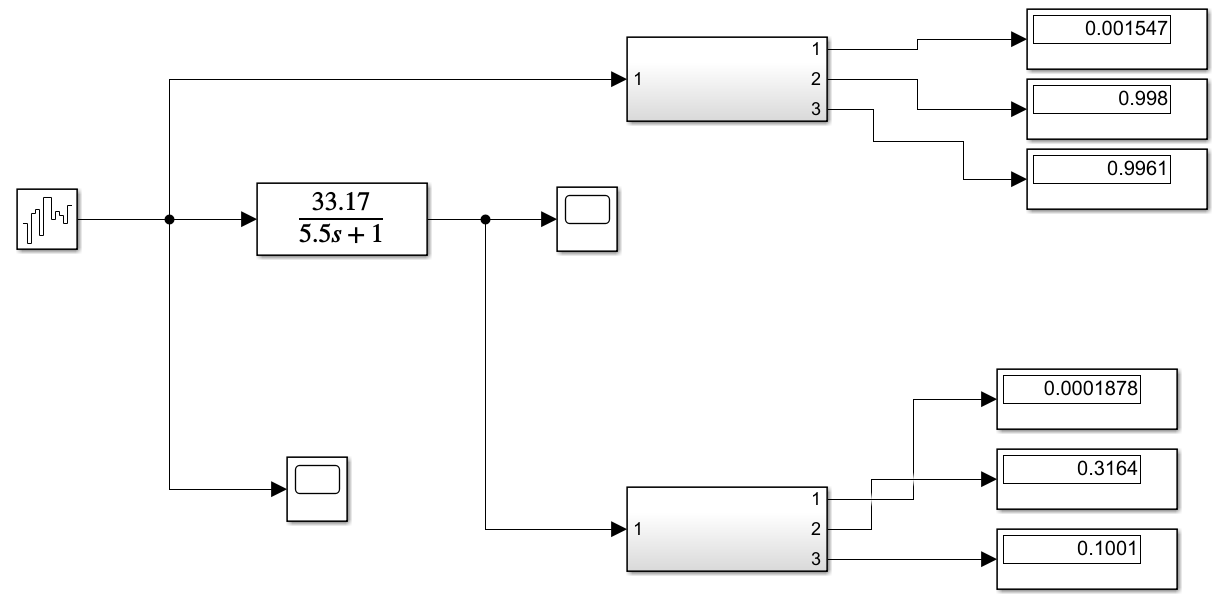
Рис.1 – Схема модели в Matlab

Подсистема (Subsystem) изображена на рисунке 2.

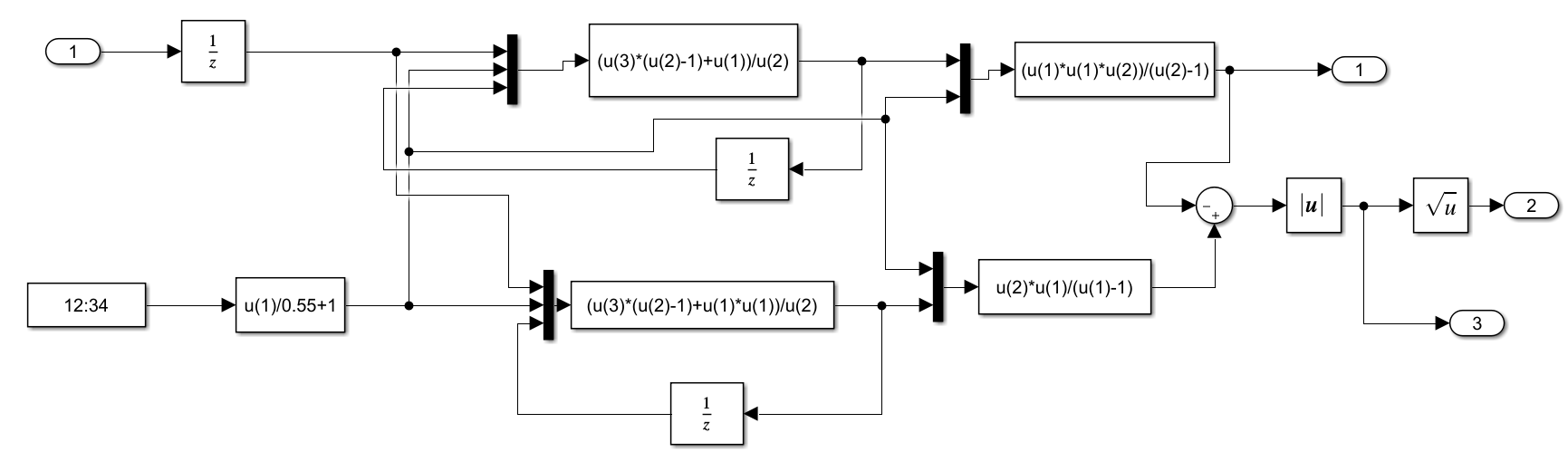
Рис.2 – Модель подсистемы

В результате моделирования получили значение дисперсии 0,1001. По теоретическим расчётам дисперсия равна 0,1.

Погрешность рассчитаем по формуле:

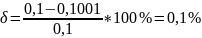
Вывод:

Из проделанной работы, можно сказать, что модель работает корректно, т.к. погрешность лежит в допустимых пределах (0,1%) и достоверности полученных результатов.