Лабораторные / ДГМ_3_20в_6408_НуртазинИ

МИНистерство науки и высшего образования РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

отчёт

по практической работе №3

по дисциплине «Дополнительные главы математики»

Тема: Параметрическая оптимизация системы управления электромеханическим объектом со случайным возмущением

Вариант 20

Студент гр. 6408		Нуртазин И.
Преподаватель		Туркин Д. Н.

Санкт-Петербург

2021

Цель работы:

Получение практических навыков решения задачи параметрической оптимизации систем управления электромеханическими объектами со случайными возмущениями.

Основные теоретические положения:

Рассматривается следящая система двухмассового упругого электромеханического объекта, на который действует случайное возмущающее воздействие 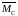с характеристикой спектральной плотности вида 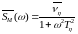. Управляющим является эквивалентное синусоидальное воздействие вида 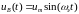. Ошибка слежения в этом случае представляет собой случайный процесс, поэтому при проектировании таких систем стремятся обеспечить минимум средней квадратической ошибки наведения в процессе функционирования, то есть:

,

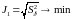где 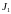– функционал качества работы системы; 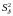– оценка дисперсии ошибки слежения.

Однако, если в качестве критерия качества работы системы принимается минимум , это всегда приводит к такому подбору параметров системы, при которых она будет находиться на границе устойчивости, что практически неприемлемо. Поэтому при решении такой задачи функционал качества следует формировать в виде .

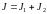Следящая система состоит из двух контуров регулирвоания: контура скорости и контура положения. Считается, что быстродействие внутреннего токового контура настолько велико, что его динамическими характеристиками можно пренебречь. Кроме того, можно принебречь и влиянием обратной связи по тротиво-эдс на работу токогово контура.

Структурная схема поиска функционала приведена на рисунке 1.

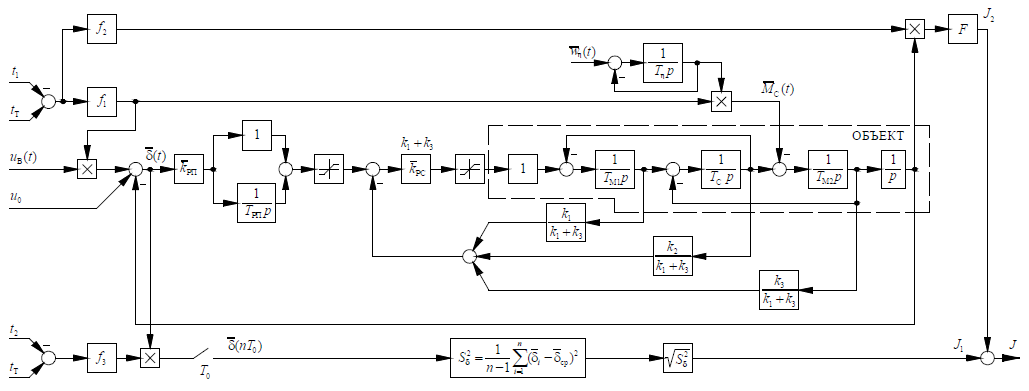
Рисунок 1 – Структурная схема поиска функционала J

Скоростная подсистема выполняется по принципам модальног управления. В соотвествии с этим в работе необходимо определить значения коэффициентов модального регулятора .

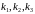Контур положения настраивается за счет выбора параметров 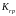и 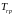пропорционально-интегрального регулятора.

В работе требуется определить такие значения параметров ПИ-регулятора положения и , которые обеспечат минимум функционалу .

Численные значения параметров параметров, характеризующих объект управления для варината 20 приведены в табилице 1.

Таблица 1 – Численные значения параметров

Вариант №	Параметры объекта управления
20	2.25	6.6	0.25	100

Ход работы:

Структурная схема оптимальной системы управления объектом приведена на рисунке 2.

Рисунок 2 – Структурная схема оптимальной системы

В представленной структурной схеме содержаться следующие подсистемы:

Subsystem – передаточная функция регулятора (рисунок 3);

Subsystem 1 – передаточная функция неизменяемой части системы (рисунок 4);

Subsystem 2 – вычисление (рисунок 5);

Subsystem 3 – фильтр для формирования требуемой спектральной характеристики возмущающего воздействия (рисунок 6);

Subsystem 4 – расчет второго слагаемого функционала качества (рисунок 7);

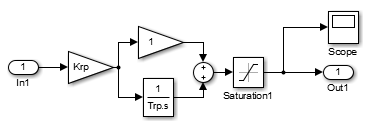
Рисунок 3 – Subsystem

Рисунок 4 – Subsystem 1

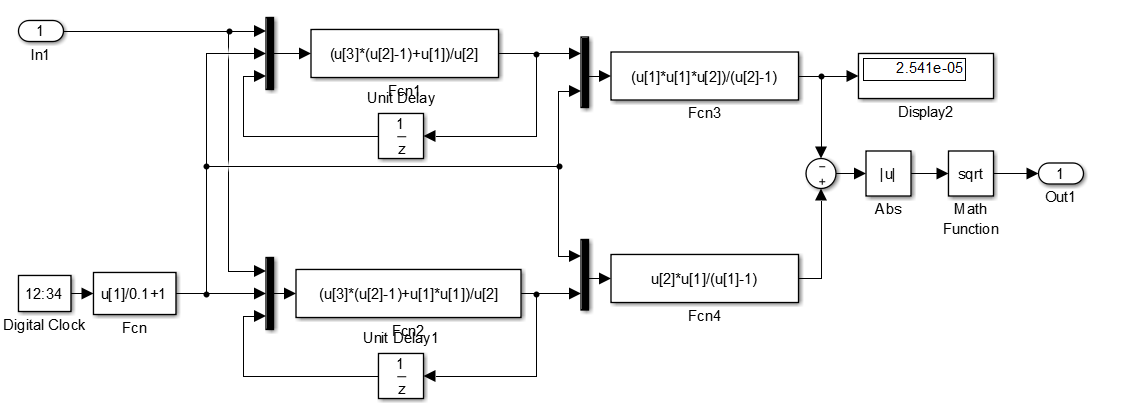
Рисунок 5 – Subsystem 2

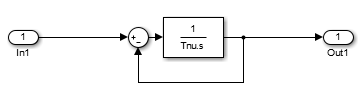
Рисунок 6 – Subsystem 3

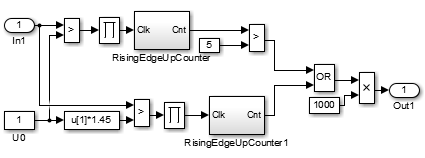
Рисунок 7 – Subsystem 4

Для определение коэффициентов выполним следующие операции:

Определение матриц A и B

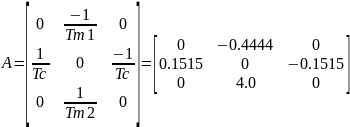
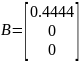
Определение коэффициентов регулятора:

Характеристический полином:

,

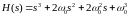где 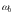– параметр, характеризующий, возникновение колебаний в системе.

Для возврата строки коэффициентов модального регулятора воспользуемся функцией 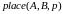, где 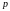– строка корней характеристического полинома.

Определим методом подбора, таким образом, чтобы ограничение соответствующих переменных не приводило бы к возникновению колебаний в системе. Для определения качества подбора обратимся к подсистеме Subsystem 1 и произведем оценку осциллограмм (рисунок 8 – 11).

Рис. 8 – Осциллограмма при

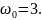
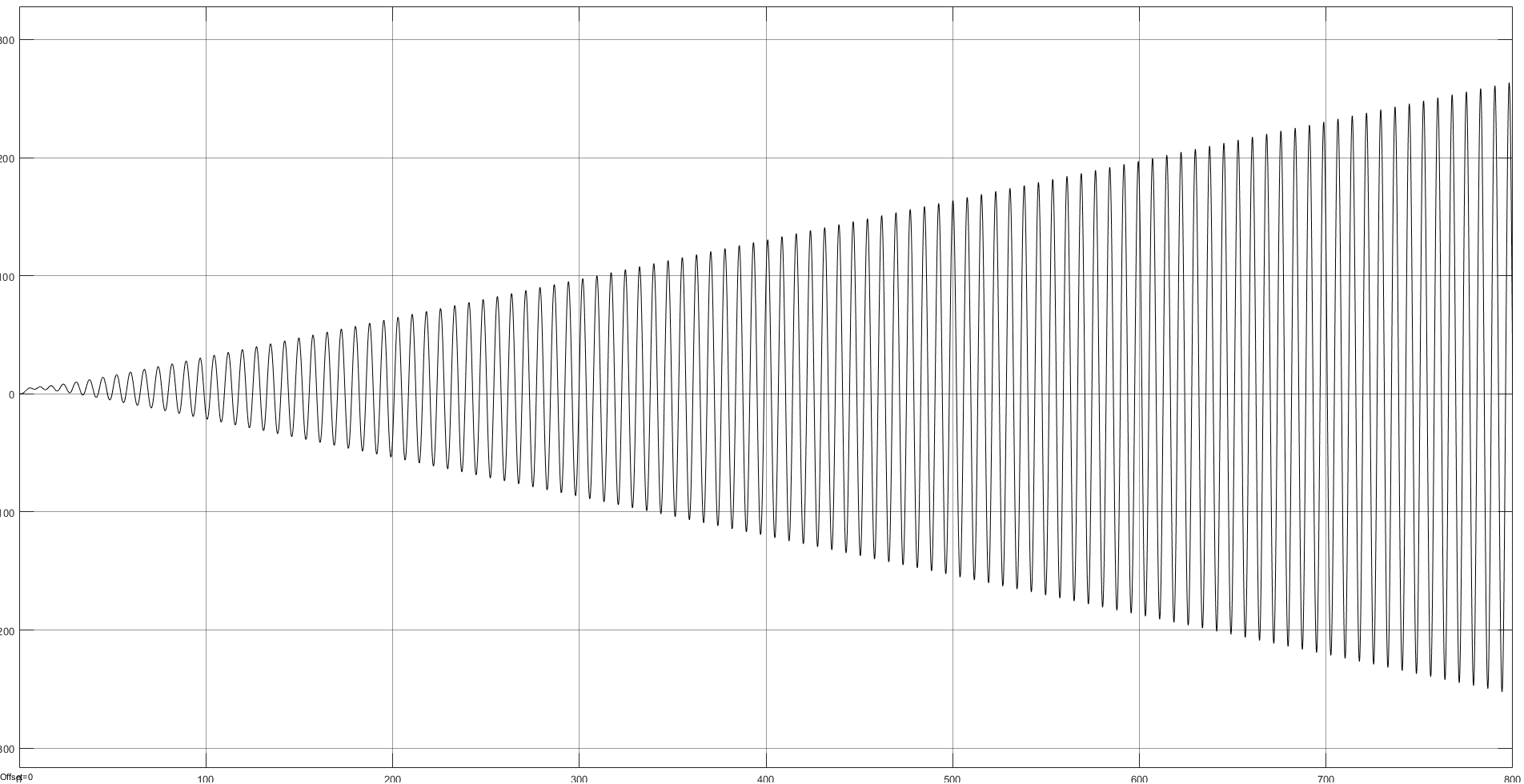
Рис. 9 – Осциллограмма при

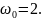
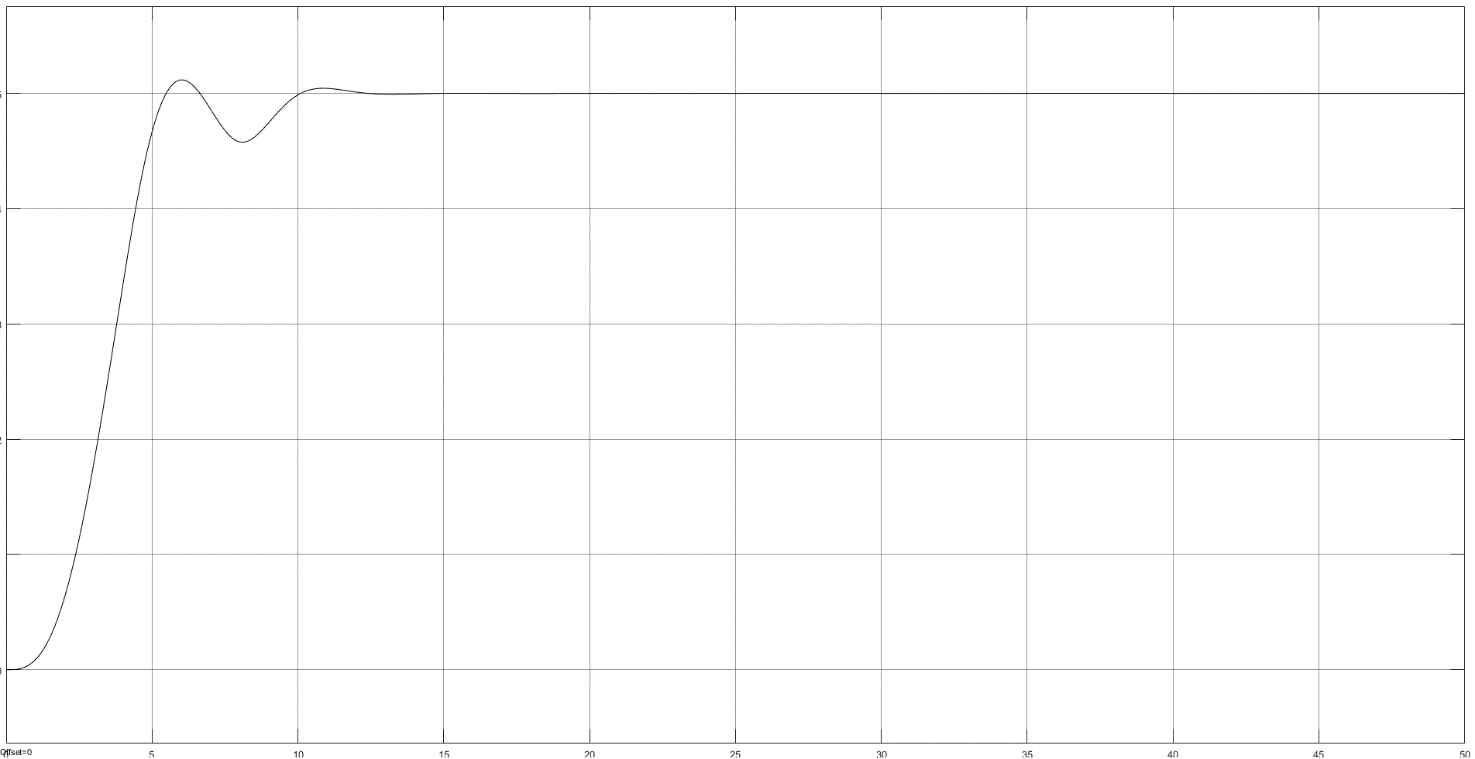
Рис. 10 – Осциллограмма при

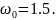
Рисунок 11 – Осциллограмма при

Выбираем значение 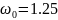, на мой взгляд оно является оптимальным (наименьшее время перерегулирования, наименьшая колебательность). В дальнейших расчётах принимаем

Коэффициенты регулятора:

Поиск коэффициентов и методом ЛАФЧХ представлен на рисунке 12.

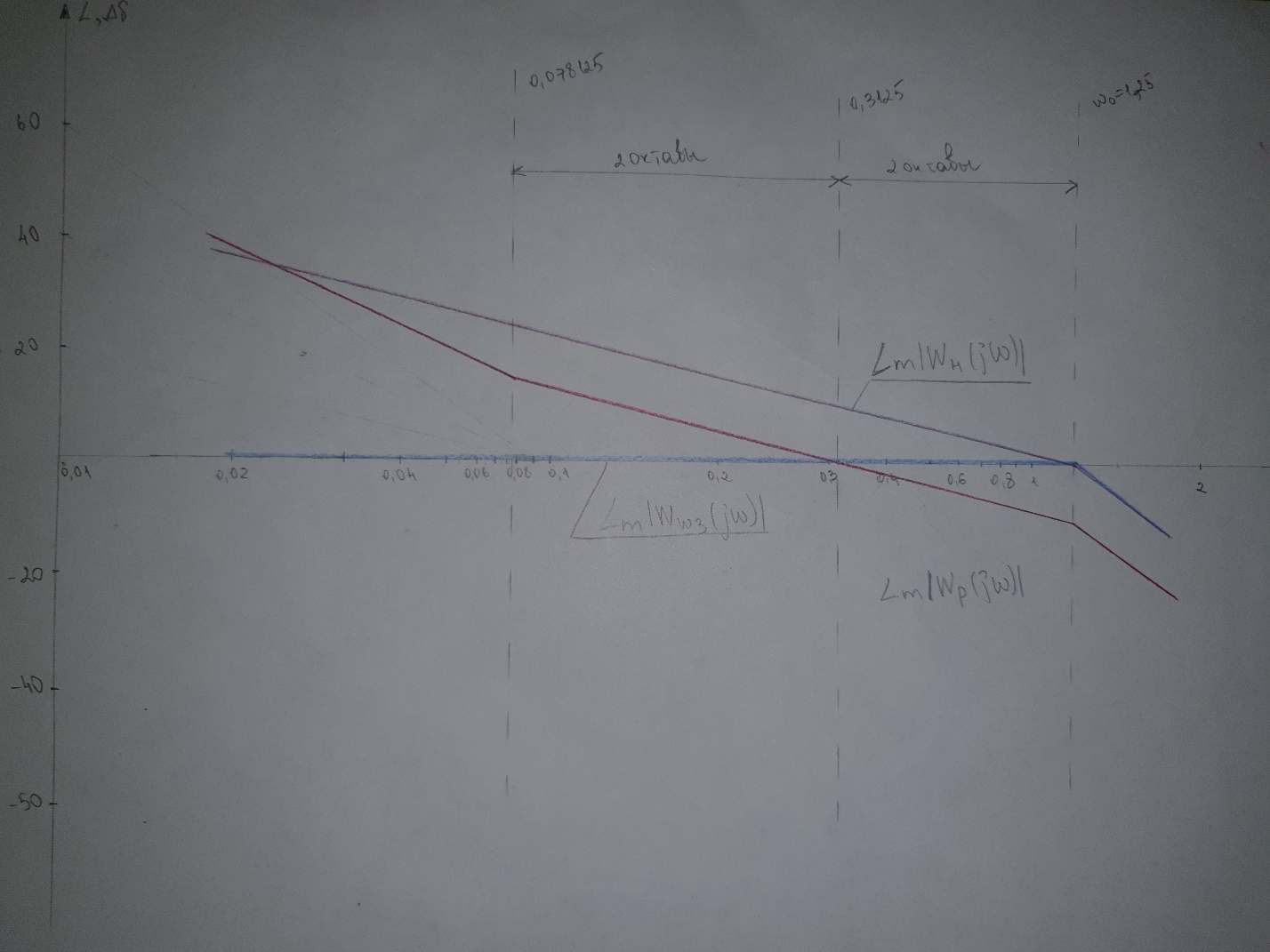
Рис. 12 – Поиск коэффициентов и

Согласно построенным характеристикам определяем коэффициенты и :

;

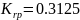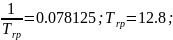
Далее, воспользуемся методом деформированного многогранника для минимизации функционала J.

x = minsearch(fun, x0,△x,wait, [options]),

где х – l-мерный вектор, fun – функция, которая принимает вектор x и возвращает скаляр f, х0 – вектор начальных значений варьируемых параметров, △x – вектор шагов варьирования параметров, wait – если 1 – то переход на следующую итерацию осуществляется по усмотрению пользователя, если 0 – то оптимизация происходит автоматически, options – параметры оптимизационных опций.

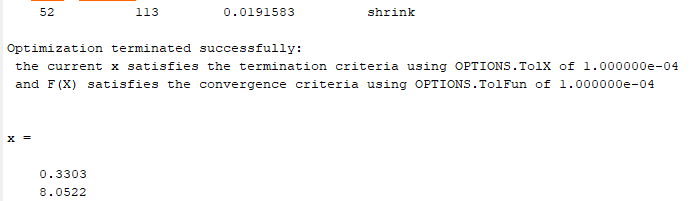
Рис. 13 – Результаты оптимизации

Выполнение поиска минимума функционала J привело к следующим результатам (таблица 2):

Таблица 2 – Результаты оптимизации

Состояние процесса	Значения коэффициентов регулятора положения	Значение функционала качества J
До оптимизации	;	J=0,021823
После оптимизации	;	J=0,0191583

Оптимальное значение достигнуто на 52 итерации.

Выводы:

В ходе данной практической работы было получено минимальное значение средней квадратичной ошибки наведения. Были найдены коэффициенты и методом ЛАФЧХ. В ходе работы были получены их оптимальные значения с помощью метода деформированного многогранника.

Значение исходного функционала с помощью функции minsearch уменьшилось на 0,0026647.

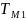
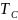
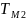
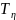
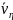
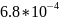
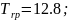
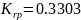11