И.З. №1

Индивидуальное задание по астрофизике №1

Вариант №1

1. Чему равна разность видимых звездных величин двух звезд, если блеск одной звезды больше блеска другой в 10 000 раз?

Решение

Воспользуемся формулой Погсона, связывающей разность звездных величин и отношение их блесков:

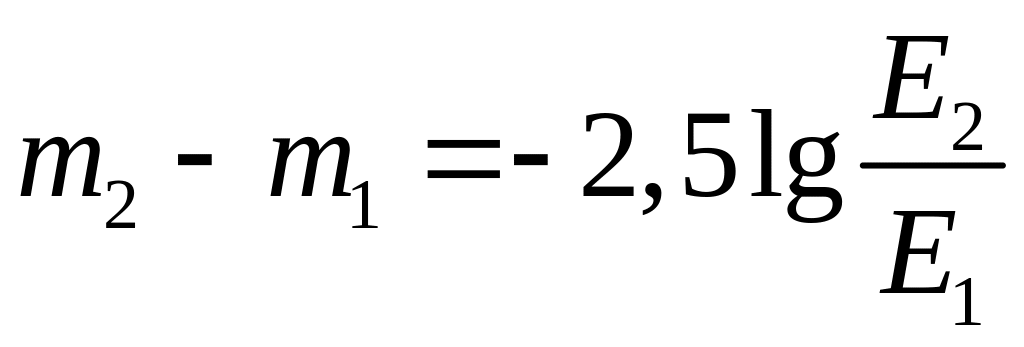
По условию, 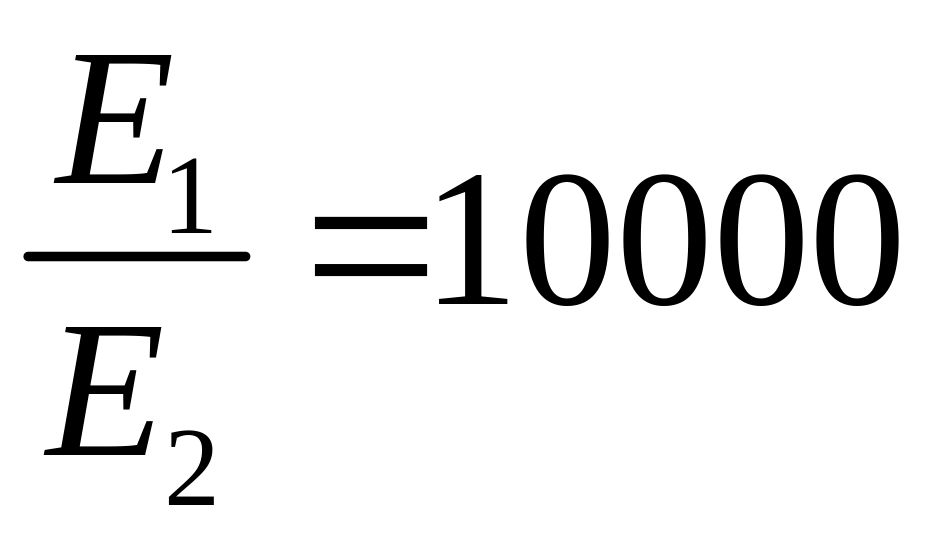, тогда ,

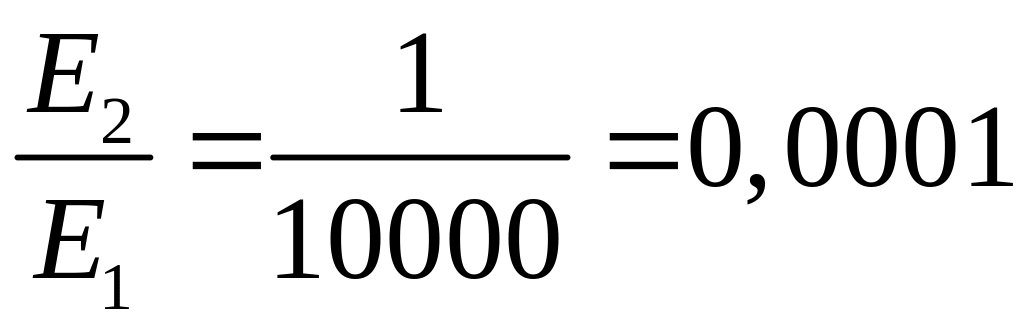Ответ: разность звездных величин 10^m.

2. Вычислите абсолютную звездную величину Сириуса, зная, что его параллакс 0,375", а видимая звездная величина –1,5^m.

Решение

Зная параллакс звезды =0,375", находим расстояние до нее в парсеках:

.

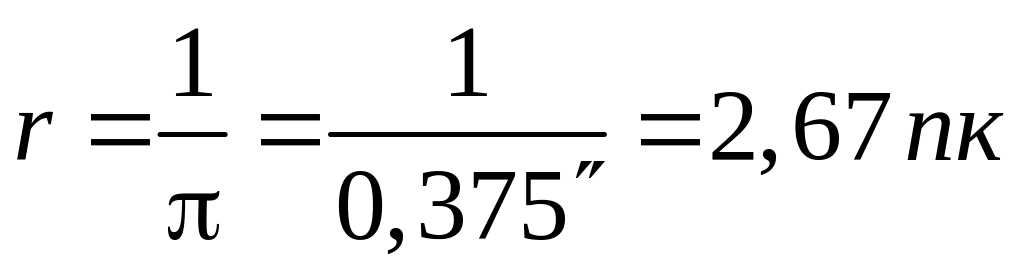Для нахождения абсолютной звездной величины воспользуемся формулой, связывающей ее с видимой величиной и расстоянием до звезды:

,

где расстояние r выражено в парсеках.

Ответ: абсолютная звездная величина Сириуса 1,4^m.

3. Определите звездное время S верхней кульминации точки весеннего равноденствия .

Решение

Момент верхней кульминации точки весеннего равноденствия принимается за начало звездных суток, следовательно, звездное время в этот момент S=0^h00^m.

Ответ: S=0^h00^m.

4. Определите часовой угол t Солнца 21 июня в момент, когда S=18^ч.

Решение

Звездное время в любой момент времени равно прямому восхождению какого-либо светила плюс его часовой угол:

.

Отсюда часовой угол светила

.

21 июня Солнце находится вблизи точки летнего солцестояния, которое наступает 22 июня. Его прямое восхождение в точке летнего солцестояния равно 90° или 6^h. За сутки прямое восхождение Солнца увеличивается примерно на 4^m, тогда 21 июня для Солнца α=6^h–4^m=5^h56^m. Для часового угла получим:

.

Ответ: часовой угол Солнца t=12^h04^m или 181°.

5. Определите условие верхней кульминации для светила, если δ  0; δ  φ.

Решение

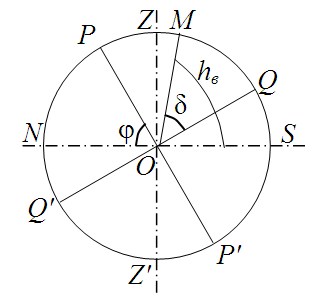
Рассмотрим сечение небесной сферы плоскостью небесного мередиана. На рисунке ZZ' – отвесная линия, NS – полуденная линия, PP' – ось мира, QQ' – линия пересечения с плоскостью небесного экватора. Поскольку высота полюса мира над горизонтом равна географической широте места наблюдения, . В момент верхней кульминации светило М находится на небесном меридиане (ближе к точке Q). Склонение светила отсчитывается от экватора в плоскости меридиана, тогда . По условию, δ>0 (светило находится в северном полушарии), |δ| < |φ|. Поскольку (как углы со взаимно перпендикулярными сторонами), то , т.е. светило в верхней кульминации находится к югу от зенита. Высота светила в верхней кульминации при этом определяется углом .

Из рисунка видим, что

.

При этом

,

откуда

.

Для зенитного расстояния получаем:

.

Ответ: условие верхней кульминации для светила с заданным δ: или .

6. Незаходящая звезда имела высоту в нижней кульминации h_н=27⁰ и h_в=71⁰ в верхней к северу от зенита. Найти склонение δ этой звезды и широту φ места наблюдения.

Решение

Запишем условие для высоты светила в нижней кульминации

и для высоты в верхней кульминации, происходящей к северу от зенита

.

Складывая эти равенства, получим:

,

Склонение звезды находим из одного из соотношений:

,

Ответ: δ=68°, =49°.

7. Через какое время по звездным часам после верхней кульминации звезды наступает ее нижняя кульминация?

Решение

В момент верхней кульминации часовой угол светила равен нулю: t₁=0, а звездное время

,

α – прямое восхождение звезды.

В момент нижней кульминации часовой угол звезды t₂=180° или t₂=12^h, звездное время

.

Следовательно, до момента нижней кульминации по звездным часам проходит 12^h.

Ответ: от верхней до нижней кульминации звезды по звездным часам проходит 12^h.

8. Долгота города Сумы равна 2^ч19^м. Определите разность местного и поясного времени в нем.

Решение.

Город Сумы находится во втором часовом поясе, который распложен примерно между долготами 1^h30^m и 2^h30^m. Центральный мерединан пояса, время которого и принимается за поясное время, имеет долготу 2^h. Следовательно, разность местного и поясного времени составляет 19^m (поскольку пункт расположен восточнее центрального меридиана пояса, местное время опережает поясное).

Ответ: местное время опережает поясное на 19^m.

9. Определите географическую долготу пункта наблюдения, если верхняя кульминация Солнца на его меридиане наблюдалась 20 ноября в 15^ч по киевскому времени. Уравнение времени в этот день было равно η=– 14^м30^с.

Решение

В момент верхней кульминации Солнца на мередиане наблюдения наступает истинный полдень, т.е. . Среднее солнечное время в том же месте связано с истинным уравнением времени:

.

Местное среднее солнечное время любого пункта равно всемирному времени (времени на Гринвиче) плюс долгота данного пункта:

.

Для киевского времени (времени второго часового пояса) имеем:

.

Вычитая эти равенства, получаем:

,

откуда

.

Знак указывает, что пункт наблюдения находится к западу от Гринвича. Переводя часовые единицы в угловые, получаем:

.

Ответ: долгота пункта 18°37'30" к западу от Гринвича.

10. В какой фазе находилась Луна в день летнего солнцестояния, если ее прямое восхождение было равно 11 часов 50 минут?

Решение

В день летнего солнцестояния прямое восхождение Солнце равно 6^h. Прямое восхождение Луны отличается от солнечного на . При этом прямое восхождение Луны больше, чем Солнца, следовательно, она находится восточнее Солнца (прямое восхождение отсчитывается от точки весеннего равноденствия против направления вращения небесной сферы, т.е. к востоку). Поскольку разность восхождений близка к 6^h или 90°, Луна находится почти в восточной квадратуре, что соответствует первой четверти.

Ответ: фаза Луны близка к первой четверти.