
Лабы КЭТ 2й семестр / 9205_Ромашкин_Лаб_3_КЭТ
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В. И. Ульянова (Ленина)
Кафедра МНЭ
отчет
по лабораторной работе №3
Тема: «Исследование переменных резисторов и конденсаторов»
Студент гр. 9205 |
|
Ромашкин В.Г. |
Преподаватель |
|
Пермяков Н.В. |
Санкт-Петербург
2021
Основные понятия и определения.
Переменный
резистор в общем случае имеет три вывода
– два из них закреплены на концах
резистивного элемента (неподвижные
контакты), а третий – соединен с подвижным
контактом, перемещающимся по резистивному
элементу. Переменное сопротивление
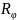 ,
соответствующее перемещению подвижной
части от 0 до φ, измеряют между подвижным
контактом и одним из неподвижных
контактов. Резистивный элемент может
быть выполнен в виде подковы, по которой
перемещается подвижный контакт (в этом
случае угол φ – поворота оси, связанной
с подвижным контактом), либо в виде
прямоугольника (φ – линейное перемещение
движка). Известны также многооборотные
переменные резисторы, в которых
перемещение подвижного контакта
осуществляется вращением регулировочного
винта; при этом полный цикл регулирования
достигается за несколько десятков
оборотов винта.
,
соответствующее перемещению подвижной
части от 0 до φ, измеряют между подвижным
контактом и одним из неподвижных
контактов. Резистивный элемент может
быть выполнен в виде подковы, по которой
перемещается подвижный контакт (в этом
случае угол φ – поворота оси, связанной
с подвижным контактом), либо в виде
прямоугольника (φ – линейное перемещение
движка). Известны также многооборотные
переменные резисторы, в которых
перемещение подвижного контакта
осуществляется вращением регулировочного
винта; при этом полный цикл регулирования
достигается за несколько десятков
оборотов винта.
Основной
функциональной характеристикой
переменного резистора является закон
регулирования – зависимость относительного
изменения сопротивления
/
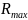 от относительного перемещения подвижного
контакта φ /
от относительного перемещения подвижного
контакта φ /
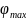 ,
где
– максимальное перемещение (угловое
или линейное) подвижного контакта;
– сопротивление резистивного элемента
(
,
где
– максимальное перемещение (угловое
или линейное) подвижного контакта;
– сопротивление резистивного элемента
(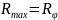 при
при
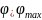 ).
).
По характеру закона регулирования переменные резисторы разделяют на линейные и нелинейные (логарифмические, обратнологарифмические, S-образные и т. Д.).
Линейный закон регулирования может быть записан в виде
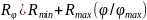 ,
,
где
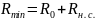
Часто встречаются резисторы с логарифмическим законом регулирования:
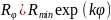 ,
Сделал Ромашкин
,
Сделал Ромашкин
Максимальное сопротивление переменного резистора (сопротивление резистивного элемента) называют номинальным сопротивлением, которое обычно выбирают из ряда Е6 (см. табл. П.1). Для резисторов с угловым перемещением подвижного контакта и пленочным резистивным элементом
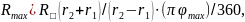
где
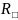 – сопротивление квадрата резистивной
пленки;
– сопротивление квадрата резистивной
пленки;
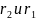 – внутренний и наружный радиусы
резистивного элемента;
- угол между контактами резистивного
элемента, … ◦.В большинстве переменных
и подстроечных конденсаторов регулирование
емкости обеспечивается изменением
площади перекрытия обкладок. Одна
обкладка (или система обкладок) находится
на вращающейся части конденсатора
(ротор), а другая (статор) – неподвижна.
– внутренний и наружный радиусы
резистивного элемента;
- угол между контактами резистивного
элемента, … ◦.В большинстве переменных
и подстроечных конденсаторов регулирование
емкости обеспечивается изменением
площади перекрытия обкладок. Одна
обкладка (или система обкладок) находится
на вращающейся части конденсатора
(ротор), а другая (статор) – неподвижна.
Протокол
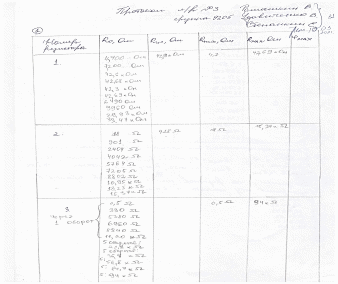 Таблица
3.1.1
Таблица
3.1.1
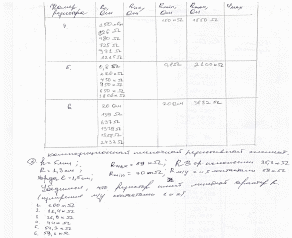 Таблица
3.1.1(продолжение)
Таблица
3.1.1(продолжение)
Таблица 3.2.1

Обработка результатов.
1.
Пользуясь данными, полученными в пункте
3.3.1, по таблице 3.1.1 построить зависимости
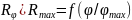 для всех исследованных резисторов.
для всех исследованных резисторов.
Для резисторов с линейным законом регулирования определить точность соблюдения закона (в процентах).
Для резистора с логарифмическим законом регулирования определить
постоянную k в выражении 3.1 [ ].
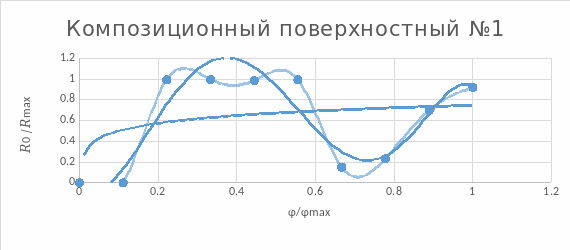
Рисунок 3.1.1
Нелинейный
закон регулирования. k
=
ln(
)/(ln(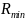 )*
)*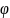 )
= -0,00449
)
= -0,00449
Рисунок 3.2.1
Нелинейный закон регулирования. k = ln( )/(ln( )* ) = -0,00399
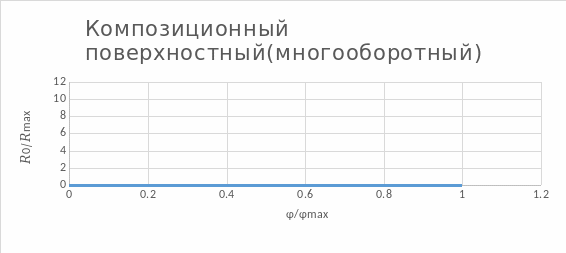
Рисунок 3.3.1
Линейный закон регулирования. Точность соблюдения закона = 96,4%.
Рисунок 3.4.1
Линейный закон регулирования. Точность соблюдения закона = 97,5%
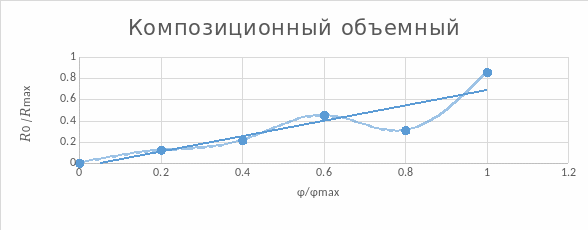
Рисунок 3.5.1
Линейный закон регулирования. Точность соблюдения закона = 91,5%
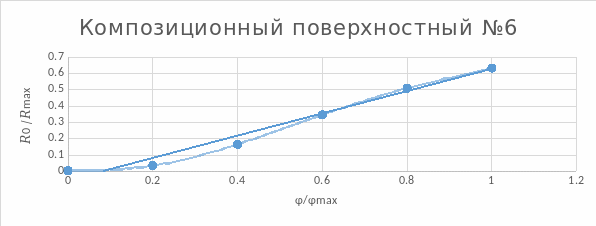
Рисунок 3.6.1
Линейный закон регулирования. Точность соблюдения закона = 97,1%
2.
По
результатам измерений, полученных в
З.З.2, пользуясь выражением
(3.2) [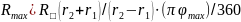 ],
рассчитать сопротивление квадрата
пленочного резистивного. Определить
номинальное сопротивление исследованного
резистора. Результаты занести в таблицу
3.3.
],
рассчитать сопротивление квадрата
пленочного резистивного. Определить
номинальное сопротивление исследованного
резистора. Результаты занести в таблицу
3.3.
|
|
, …◦ |
, Ом |
|
|
, Ом |
|
16 |
25 |
260 |
59000 |
35300 |
59000 |
6312,7 |
6340 |
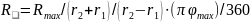
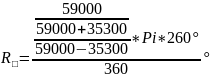
3.
Пользуясь
данными, полученными в пункте 3.3. построить
зависимости
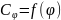 для воздушного и керамического
конденсаторов. Определить точность
соблюдения закона регулирования. Для
подстроечного керамического конденсатора
определить
для воздушного и керамического
конденсаторов. Определить точность
соблюдения закона регулирования. Для
подстроечного керамического конденсатора
определить
 по
данной зависимости.
по
данной зависимости.
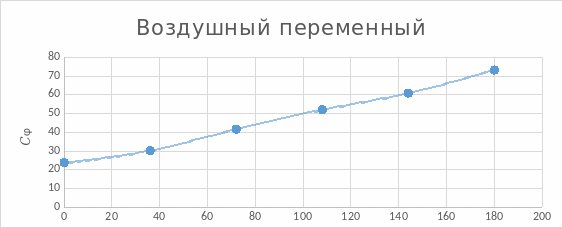
Рисунок 3.7.1
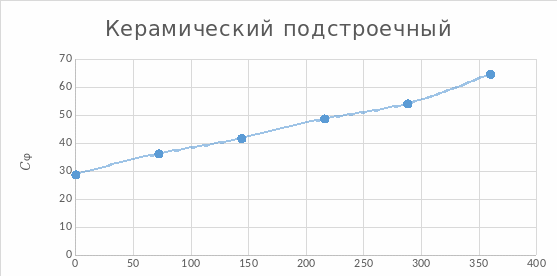
Рисунок 3.8.1
По
графику найдем углы
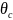 и
и
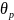 .
При повороте ротора изменение емкости
происходит по линейному закону на
участке, ограниченном
и
.
Участок графика, более соответствующий
линейной зависимости, находится в
пределах от 216◦ до 288◦. Следовательно,
.
При повороте ротора изменение емкости
происходит по линейному закону на
участке, ограниченном
и
.
Участок графика, более соответствующий
линейной зависимости, находится в
пределах от 216◦ до 288◦. Следовательно,
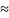 216◦;
216◦;
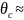 288◦
288◦
4.
Рассчитать температурные коэффициенты
сопротивления двух исследованных
резисторов по формуле
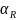 =
(1/ R0)[(R-
R0)/(t-
t0)]
и
температурный коэффициент емкости
конденсатора по формуле
=
(1/ R0)[(R-
R0)/(t-
t0)]
и
температурный коэффициент емкости
конденсатора по формуле
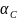 =
(1/ С0)[(С-
С0)/(t-
t0)].
=
(1/ С0)[(С-
С0)/(t-
t0)].
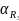 =
(1/17994)
[(178300 - 17994)/ (65- 20)] = -0,0002026
=
(1/17994)
[(178300 - 17994)/ (65- 20)] = -0,0002026
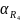 =
(1/45215)
[(45220 - 45215)/ (65- 20)] = 0,00000246
=
(1/45215)
[(45220 - 45215)/ (65- 20)] = 0,00000246
= (1/ 46) [(46,1- 46)/ (65- 20)] = 0,0000483
Вывод.
В ходе выполнения данной лабораторной работы, нами были исследованы параметры различных переменных резисторов и конденсаторов.
Первым делом был проведен ряд измерений сопротивления переменных резисторов с логарифмическим законом регулирования. Была определена величина k, для первого образца она составила -0,00449, а для второго -0,00399. По всей видимости, чем больше k, тем сильнее проявляются свойства нелинейности резистора. Образец № 2 повел себя странно, вместо логарифмической зависимости мы наблюдаем линейную, это произошло вероятнее всего из-за ошибки при снятии показаний.
Резисторы с линейной зависимостью повели себя гораздо более предсказуемо, кроме образца №5, у которого одно из показаний нарушает общую картину линейности, по всей видимости произошла осечка, показания были сняты не точно. Закон регулирования был соблюден с точностью порядка 90%.
Было
рассчитано сопротивление
квадрата пленочного резистивного
элемента, определено номинальное
сопротивление из номинального ряда
Е96: 634*10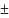 0,5%
, полученное нами сопротивление 6312,7 Ом
соответствует данному диапазону.
0,5%
, полученное нами сопротивление 6312,7 Ом
соответствует данному диапазону.
Для воздушного переменного и подстроечного конденсатора были найдены углы поворота для ротора и статора ( 216◦; 288◦).
В добавок к этому были посчитаны температурные коэффициенты сопротивления для третьего и четвертого резисторов, -2,026*10^-4 и 2,46*10^-6 соответственно. У третьего резистора ТКС отрицательный, следовательно, его сопротивление падает при нагревании. Емкость конденсатора медленно повышается при нагревании (ТКС=4,83*10^-5).

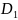 =
2
=
2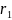 ,
мм
,
мм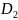 =2
=2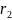 ,
мм
,
мм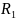 ,
Ом
,
Ом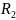 ,
Ом
,
Ом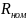 ,
Ом
,
Ом