
Мансуров. Основы программирования в среде Lazarus. 2010
.pdf
Глава 1 Основы программирования
____________________________________________________________________
a33 a33 m3a13
b3 b3 m3b1
Уравнение (3) приобретает вид:
a32 x2 a33 x3 b3 |
(5) |
И исходная система (1.21) теперь имеет вид:
a11x1+a12x2+a13x3=b1 |
(1) |
|
||
a22 x2 |
a23 x3 |
b2 |
(4) |
(1.28) |
a32 x2 |
a33 x3 |
b3 |
(5) |
|
Эти новые уравнения эквивалентны исходным, с тем преимуществом, что |
||||
x1 не входит ни во второе, ни в третье уравнение системы. |
|
|||
Попытаемся теперь исключить x2 из уравнений (4) и (5). |
|
|||
Если a22 0 , то мы вновь снова переставим местами уравнения, так чтобы |
||||
a22 0 . Если же a22 |
0 и a32 |
0 , то система вырождена и либо не имеет ре- |
||
шения, либо имеет бесконечное множество решений. Введем новый множитель
m |
|
a3 2 |
. Умножим его на (4) и вычтем его из (5) |
|
3 |
a2 2 |
|
||
|
|
|
||
|
|
|
|
|
|
|
|
(a32 m3 a22 )x2 (a33 m3a23 )x3 b3 b2 m3 |
(1.29) |
В силу выбора m3
a32 m3 a22 0
a33 a33 m3 a23 |
(1.30) |
b3 b3 b2 m3
Уравнение (1.29) запишется в виде
41

1.3 Примеры разработки алгоритмов
____________________________________________________________________
a33 x3 b3 |
(1.31) |
Уравнение (1.29) можно заменить уравнением (1.31).
Система (1.21) приобретает вид:
a11x1+a12x2+a13x3=b1 |
(8) |
|
|
a22 x2 a23 x3 |
b2 |
(9) |
(1.32) |
a33 x3 |
b3 |
(10) |
|
Решение этой системы совершенно очевидно.
x3 |
b3 |
|
a33 |
||
|
|
|
|
x2 |
a23 x3 |
|
(1.33) |
|||
|
|
|
|
b2 |
|
||||
|
|
|
|
|
|
a22 |
|
||
|
|
|
x1 |
b1 |
a12 x2 a13 x3 |
|
|
||
|
|
|
|
a11 |
|
||||
|
|
|
|
|
|
|
|||
Для |
чего мы всегда переставляем уравнения таким образом, чтобы |
||||||||
a11, a22 , a33 |
были не равны 0? Чтобы не было деления на 0! |
|
|||||||
Пример: |
|
|
|
|
|
|
|
|
|
x |
y |
z |
4 |
|
|
|
|
|
|
2x |
3y |
|
z 9 |
|
|
|
(1.34) |
||
x |
y |
z |
2 |
|
|
|
|
|
|
Умножим первое уравнение (1.34) на 2 и вычтем из 2-го уравнения. Затем первое уравнение умножим на 1 и вычтем из 3-го. Получим систему, эквива-
42

Глава 1 Основы программирования
____________________________________________________________________
лентную (1.34).
x |
y |
z |
4 |
y |
z |
1 |
(1.35) |
|
2 y |
2z |
6 |
Умножив второе уравнение (1.35) на (-2) и вычтя его из 3-го уравнения получаем
x y z 4
y z 1 |
(1.36) |
4z  4
4
Отсюда решением этой системы будет: x 1
y 2 z 1
Обобщим этот метод на случай системы из n уравнений с n неизвестными
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
|
a21 x1 |
a22 x2 |
... |
a2n xn |
b2 |
(1.37) |
|
……………………………………………… |
|
|||||
an1 x1 |
|
an 2 x2 ... |
ann xn |
bn |
|
|
Предполагается в силу расположения уравнений a11 ≠0. Введем n-1 |
||||||
множителей: |
|
|
|
|
|
|
m |
ai1 |
, |
i = 1, 2, 3, … n |
(1.38) |
||
|
||||||
i |
a11 |
|
|
|
|
|
|
|
|
|
|
||
И вычтем из каждого i-го уравнения первое, умноженное на mi. Обозначим
aij aij mi a1 j ,
43

1.3 Примеры разработки алгоритмов
____________________________________________________________________
bi bi mi b1 |
, |
|
|
|
(1.39) |
|
i=2, 3, …, n, |
j=1, 2, …, n |
|
|
|||
Для всех уравнений, начиная со 2-го ai1 =0, i=2, 3, … n |
|
|||||
Получим систему |
|
|
|
|
|
|
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
|
0 a22 x2 |
... |
a2n xn |
b2 |
(1.40) |
||
……………………………………………… |
|
|
||||
0 |
an 2 x2 |
... |
ann xn |
bn |
|
|
Продолжая таким образом, мы можем исключить x2 из последних n-2
уравнений, x3 из последних n-3 уравнений и т.д. На некотором k-ом этапе мы исключим xk с помощью множителей.
|
(k 1) |
a (k 1) |
i=k+1,…n |
|
(1.41) |
|||
|
mi |
akk (k 1) , |
|
|||||
|
|
ik |
|
|
|
|
|
|
Причем |
|
|
|
|
|
|
|
|
a( k 1) |
0 , |
|
|
|
|
|
|
|
kk |
|
|
|
|
|
|
|
|
a(k ) |
a(k 1) |
m(k 1) a |
(k 1) |
|
|
|
|
|
ij |
ij |
i |
kj |
|
|
|
|
|
b( k ) |
b( k 1) |
m( k 1)b( k 1) |
|
|
|
|
||
i |
i |
i |
k |
|
|
|
|
|
где i = k+1, k+2,…, n; |
j = k,…, n; |
k = 1,…, n-1 |
|
|||||
Окончательно треугольная система уравнений записывается следующим |
||||||||
образом. |
|
|
|
|
|
|
|
|
|
|
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 |
|
|
|
|
|
a22 x2 |
... |
a2n xn |
b2 |
(1.42) |
|
44

Глава 1 Основы программирования
____________________________________________________________________
……………………….
|
|
|
|
|
|
|
|
|
|
|
|
a( n |
1) x |
|
b( n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
n |
n |
Обратная подстановка для нахождения значений неизвестных задается |
||||||||||||||||
формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
b( n |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a ( n |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b( n 2) |
a( n |
2) |
|
x |
|
|
|
|
|
|
|
|
||
xn 1 |
|
|
n 1 |
n 1,n |
|
|
n |
|
|
|
|
|
(1.43) |
|||
|
|
|
|
a( n 2) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n 1,n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
b( j |
1) |
|
a( j 1) |
x |
j |
|
|
... a( j 1) |
x |
j 1 |
|
|
|
|
|
x j |
j |
|
|
j ,n |
|
|
|
j , j 1 |
|
, |
j=n-2, n-3,…,1 |
|||||
|
|
|
|
|
a jj |
( j 1) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
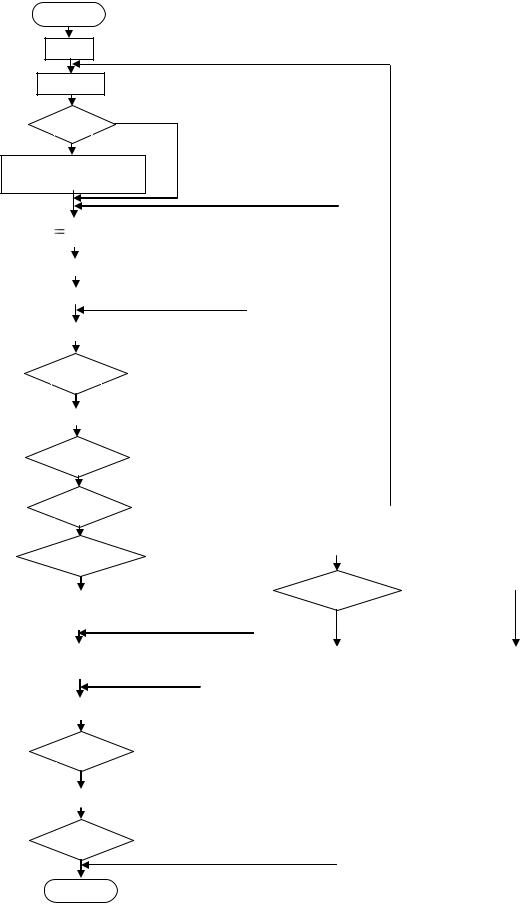
Блок-схема алгоритма показана на рис. 1.12.
Здесь, чтобы не загромождать блок-схему, мы предположили, что коэффи-
циенты системы уже введены. В этой блок-схеме неясно только одно – что зна-
чит переставить уравнение, как это сделать?
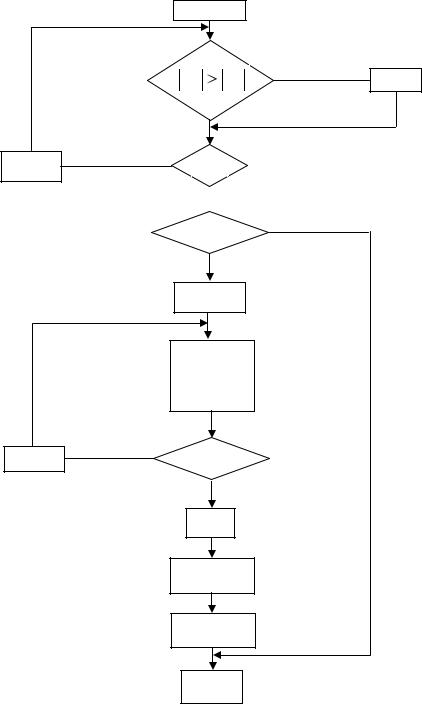
Оказывается, что если переставить уравнения таким образом, чтобы коэф-
фициент при xk был наибольшим, то ошибки округления будут минимальными.
Этот коэффициент называется главным элементом. И перестановка уравнений c
выбором главного элемента называется методом главных элементов, рис. 1.13.
45
1.3 Примеры разработки алгоритмов
____________________________________________________________________
начало
k=1
i=k+1
нет
akk=0
да
Переставить ур-е так чтобы akk≠0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m aik / akk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aik=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
j=k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aij=aij-makj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
j=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
j=j+1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
bi=bi-mbk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
i=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=i+1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
да |
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
k=n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=k+1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ann=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn=0 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
xn=bn/ann |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
i=n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=i+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система не |
|
|
|
Система имеет бесконеч- |
|||||||||||
|
|
|
|
|
|
|
|
S=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет решения |
|
|
|
ное множество решений |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S=S - aijxj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
j=n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=j+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
xi=(bi + S)/aii |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=i-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
конец |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.12. Алгоритм Гаусса |
|
|
|
|||||||||||
46
Глава 1 Основы программирования
____________________________________________________________________
i=i+1
j=j+1
l=k
|
да |
aik alk |
l=i |
нет
нет
i=n

 да
да
l=k
да
нет
j=k
t=akj
akj=alj
alj=t
нет
j=n
да
t=bk
bk=bl
bl=t
i=k+1
Рис. 1.13. Алгоритм перестановки уравнений
47
Глава 2 Введение в язык программирования Pascal
2.1. Основные элементы языка
Язык Pascal (Паскаль), изобретенный в начале 70-х годов 20-го века Н. Виртом и названный в честь французского математика и философа Блеза Паскаля, является одним из наиболее распространенных языков программиро-
вания. От других языков он выгодно отличается возможностью более ясно и логично записывать программы.
Программа на языке Паскаль состоит из двух частей: описание действий,
которые должны быть выполнены и описание данных, над которыми они вы-
полняются. В тексте программы описание данных предшествует описанию дей-
ствий. В этом выражается общее правило языка – каждый встречающийся в программе объект должен быть предварительно описан.
Описание данных состоит из описания переменных. Операторами называ-
ются действия над данными. В общем виде любая Паскаль – программа имеет вид:
заголовок программы
раздел описания переменных
раздел операторов
Заголовок программы имеет вид:
program имя программы;
Здесь слово "program" – это так называемое ключевое (или служебное или еще говорят зарезервированное) слово. Оно должно записываться именно
48
Глава 2 Введение в язык программирования Pascal
____________________________________________________________________
так (без кавычек), а не иначе. Допускается использовать как строчные, так и прописные буквы. Записи PROGRAM, Program, ProgRam – разрешены и означают одно и то же.
Так начинаются все программы, написанные на языке Паскаль. Здесь нече-
го понимать, просто так принято разработчиком языка.
В принципе допускается не использовать заголовок program, но лучше все-таки начинать программу именно с заголовка!
Имя программы – это любая последовательность букв, цифр и некоторых знаков. Такие последовательности называются идентификаторами.
Идентификатор состоит из 1-127 символов – букв, цифр или знаков подчѐрки-
вания, при этом первым должна быть буква или знак подчѐркивания. Иденти-
фикатор не должен совпадать ни с одним из ключевых слов. В идентификаторе не должно быть (.) – точки, (,) – запятой, самих скобок ( ), а также пробелов и знаков операций.
Примеры правильных идентификаторов:
Х3
Summa
VOLVO
Select_screen_color
Примеры неправильных идентификаторов:
3х начинается с цифры
Sum.ma внутри идентификатора есть точка
VOL VO есть пробел
2.1.1 Переменные. Стандартные типы.
Каждая переменная имеет имя и тип. Имя переменной – это произвольный идентификатор. В дальнейшем будем говорить "переменная х", вместо "пере-
менная с именем х".
49

2.1 Основные элементы языка
____________________________________________________________________
Тип переменной определяет множество еѐ возможных значений, набор до-
пустимых операций над переменной и размер занимаемой памяти.
В Паскале существуют следующие стандартные типы переменных: integer (целый), real (вещественный), boolean (логический), char
(символьный), string (строковый).
Значениями переменных целого типа являются целые (и только!) числа.
Примеры целых чисел:
25 |
+150 |
-200 10000 |
Операции над целыми числами таковы:
+ (сложение), - (вычитание), * (умножение), div (деление нацело), mod
(остаток от деления двух целых чисел).
Значениями переменных вещественного типа являются вещественные чис-
ла. Определены следующие операции над вещественными числами:
+ (сложение), - (вычитание), * (умножение), / (деление).
Запись вещественных чисел похожа на общепринятую, только вместо за-
пятой используется точка и вместо степени 10 используется буква Е.
Пример:
|
Таблица 2.1 |
Общепринятая |
на Паскале |
|
|
5,30 |
5.30 |
-1,0 |
-1.0 |
41000 |
41000 или 4.1Е4 |
-0,73∙10-2 |
-0.73Е-2 |
|
|
Значениями переменных логического типа является true (истина), false
(ложь). Определены операции: not (не), and (и), or (или), xor (исключающее или).
50
