
Лабраб 3 ЧМ
.docxФедеральное агентство связи
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
“Московский технический университет связи и информатики”
Кафедра информатики
ЛАБОРАТОРНАЯ РАБОТА №3
«Численное интегрирование»
по дисциплине
Численные методы
Выполнил: студент гр. БИН1907 Власов Андрей
Проверил: к.т.н., доцент Г.Сосновиков
Москва 2021 г.
ОГЛАВЛЕНИЕ
I. ЗАДАНИЕ
Общее задание, индивидуальный вариант 3
II. ВЫПОЛНЕНИЕ РАБОТЫ
Выполнение 4-6
I. ЗАДАНИЕ
Общее задание к работе
1.
Создать функцию для вычисления интеграла
по 1-му заданному методу, определяя
значения (столбец m), с шагом h0 и h0/2
![]()
2. Провести оценку погрешностей полученных результатов по правилу Рунге.
3. Написать и выполнить программу вычисления интеграла по 2-му
заданному методу с точностью 10-4.
4. Вычислить заданный интеграл с использованием функции intg пакета
Scilab.
Индивидуальный вариант задания

Рисунок 1 – Индивидуальный вариант №1
Интегрирование методом средних прямоугольников – на компьютере
Интегрирование методом Симпсона – ручной расчет
1. Задания для численного интегрирования:
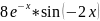 -
подынтегральная функция;
-
подынтегральная функция;
a = 2, b = 3 –пределы интегрирования;
метод интегрирования – Интегрирование методом средних прямоугольников
начальный
шаг интегрирования
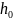 =0.25.
=0.25.
2.
Вычисление интегралов с шагом
и
/2
(
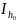 и
и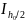 )
и оценка его погрешности по правилу
Рунге.
)
и оценка его погрешности по правилу
Рунге.
Правило Рунге применяют для вычисления погрешности путём двойного
просчёта интеграла с шагами h/2 и h, при этом погрешность вычисляется по формуле
![]()
Считается, что интеграл вычислен с точностью Е, если |R| E; тогда
I
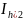 R
, где I – уточненное значение интеграла,
p – порядок метода.
R
, где I – уточненное значение интеграла,
p – порядок метода.
Вычислим интеграл по формуле средних прямоугольников и оценим погрешность интегрирования методом двойного просчёта:
![]()
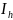
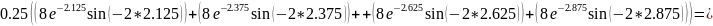 0.581472
0.581472
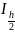
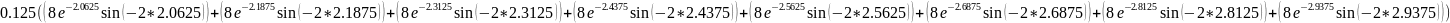 =0.578622
=0.578622
R=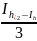 =
=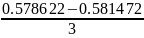 =-0.00095;
|R|<E;
=-0.00095;
|R|<E;
I=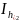 +
R = 0.578622
- 0.00095 = 0.5776
+
R = 0.578622
- 0.00095 = 0.5776
Вычислим интеграл по формуле Симпсона и оценим погрешность интегрирования методом двойного просчета:
![]()
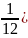 y(0)+y(4)+4(
y(1)+y(3) )+2( y(2) )) = 0.5775
y(0)+y(4)+4(
y(1)+y(3) )+2( y(2) )) = 0.5775
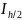
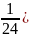 y(0)+y(8)+4(
y(1)+y(3) + y(5) +y(7) )+2( y(2) + y(4) +y(6) )) = 0.5777
y(0)+y(8)+4(
y(1)+y(3) + y(5) +y(7) )+2( y(2) + y(4) +y(6) )) = 0.5777
R=
=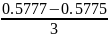 =6*10^-5
=6*10^-5
I= + R = 0.577776
3.Программа
вычисления интеграла по методу средних
прямоугольников с точностью
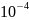 .
.

Рис. 2 – Программный код файла lab3.cpp
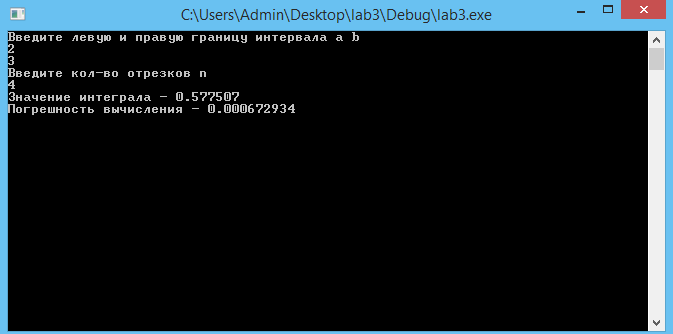
Рис. 3 – Результат работы программы
Вывод:Значение интеграла соответствует значению интеграла при вычислении с помощью средств Scilab с точностью .
4. Результаты решения, полученные с помощью функции пакета Scilab.
--> deff('y=f(x)','y=8.*exp(-x).*sin(-2.*x)');
--> a=2;b=3;
--> [s,ir]=intg(a,b,f)
s =
0.5776656
ir =
6.413D-15
