
- •1.1. Введение, теоретические сведения
- •1.2. Экспериментальная установка
- •1.3. Лабораторный эксперимент
- •1.4. Контрольные вопросы
- •1.5. Содержание отчета
- •2. ИССЛЕДОВАНИЕ СПИРАЛЬНОЙ АНТЕННЫ
- •2.1. Введение. Теоретические сведения
- •2.2. Экспериментальная установка
- •2.3. Проведение измерений
- •2.4. Контрольные вопросы
- •2.5. Содержание отчета
- •3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ РУПОРНОЙ АНТЕННЫ
- •3.1. Теоретические сведения
- •3.2. Методика измерения коэффициента усиления антенны
- •3.3. Лабораторный макет
- •3.4. Проведение измерений
- •3.5. Обработка результатов измерений
- •3.6. Контрольные вопросы
- •3.7. Содержание отчёта
- •4. ИССЛЕДОВАНИЕ ЗЕРКАЛЬНОЙ АНТЕННЫ
- •4.1. Введение. Принцип действия зеркальной антенны
- •4.2. Теоретические сведения
- •4.2. Экспериментальная установка
- •4.3. Эксперимент
- •4.4. Обработка результатов эксперимента.
- •4.5. Контрольные вопросы
- •4.6. Содержание отчета
- •5. ВЛИЯНИЕ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ НА ДИАГРАММЫ НАПРАВЛЕННОСТИ АНТЕНН
- •5.1. Идея метода зеркальных изображений
- •5.2. Применение метода зеркальных изображений к антеннам, размещенным над проводящей плоскостью
- •5.3. Обобщение на антенны с произвольно поляризованным излучением
- •5.4. Интерференция полей антенны и ее зеркального изображения
- •5.5. Частные случаи
- •5.6. Интерференционные множители
- •5.7. Экспериментальная установка
- •5.8. Проведение измерений
- •5.9. Обработка результатов и теоретические расчеты
- •5.10. Контрольные вопросы
- •5.11. Содержание отчета
- •6. ИССЛЕДОВАНИЕ МНОГОЭЛЕМЕНТНОЙ АНТЕННОЙ РЕШЕТКИ «ВОЛНОВОЙ КАНАЛ»
- •6.1. Общие сведения
- •6.2. Математическое описание вибраторных антенных решеток
- •6.2.1. Система связанных интегральных уравнений для многоэлементной антенной решетки ВК
- •6.2.2. Решение системы связанных ИУ
- •6.2.3. Метод наведенных ЭДС
- •6.3. Описание лабораторного макета
- •6.4. Задание и указания к выполнению работы
- •6.4.1. Измерение КСВ ВК1 и ВК2 в полосе частот 2…3 ГГц
- •6.4.2. Экспериментальное исследование ДН ВК1 в Е- и в Н-плоскостях на заданных дискретных частотах из интервала 2.35…2.45 ГГц
- •6.4.3. Расчет основных характеристик ВК на основе электродинамического моделирования в специализированных пакетах
- •6.5. Требования к содержанию отчета
- •6.6. Контрольные вопросы
- •7. ИССЛЕДОВАНИЕ МИКРОПОЛОСКОВОЙ АНТЕННОЙ РЕШЕТКИ
- •7.1. Общие сведения
- •7.2. Математическое описание МПА
- •7.3. Лабораторный макет
- •7.4. Программа работ
- •7.4.1. Измерение КСВ МПАР в полосе частот 3.0…4.0 ГГц
- •7.4.2. Экспериментальное исследование ДН МПАР
- •7.4.3. Расчет ДН МПАР на основе приближенной модели
- •7.4.4. Измерение отношения «вперед/назад»
- •7.4.5. Измерение ДН по кросс поляризации (выполняется по указанию преподавателя)
- •7.4.6. Расчет характеристик МПАР на основе моделирования в специализированном пакете
- •7.5. Требования к содержанию отчета
- •7.6. Контрольные вопросы
- •Список литературы
- •Оглавление
4.ИССЛЕДОВАНИЕ ЗЕРКАЛЬНОЙ АНТЕННЫ
4.1.Введение. Принцип действия зеркальной антенны
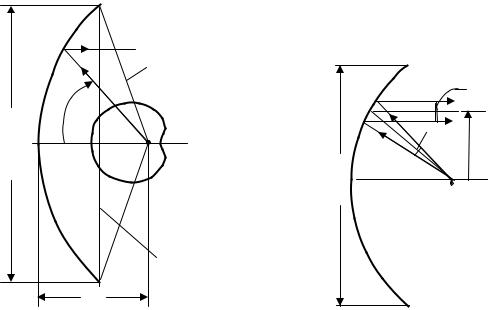
Зеркальные антенны (ЗА) – это основной тип антенн, применяемый в радиосистемах широкого назначения в тех случаях, когда требуется обеспечить простыми средствами высокую направленность (радиолокация, спутниковая связь) при минимальных тепловых потерях [7]. Нередко ЗА используются в установках с относительно медленным механическим сканированием. Идея построения остронаправленной ЗА состоит в следующем. Имеется слабонаправленный облучатель, т. е. небольшая антенна с широкой диаграммой направленности, которая облучает металлическое зеркало диаметром 2R . Профиль зеркала подбирают таким образом, чтобы в его апертуре (раскрыве) сформировалось синфазное поле. При большом отношении R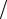 λ излучение
λ излучение
апертуры зеркала будет остронаправленным с максимумом, ориентированным вдоль оптической оси системы (рис. 4.1). Для обеспечения синфазности поля в апертуре профиль зеркала должен быть параболическим, а облучатель
|
Ψ = Ψ0 |
|
ds |
|
F0(Ψ) |
2R |
dΩ ρ |
|
2R |
|
Апертура |
|
зеркала |
F |
|
Рис. 4.1 |
Рис. 4.2 |
следует поместить в фокусе параболоида. В этом случае все радиолучи, расходящиеся из фокуса F, после отражения от зеркала пойдут параллельно фокальной оси – конический пучок лучей от облучателя преобразуется зеркалом в параллельный пучок. Поскольку поверхности равных фаз перпендикулярны семейству лучей, все они в отраженном пучке перпендикулярны фокальной оси. Следовательно, и апертура зеркала будет поверхностью равных
34
фаз, т. е. во всех точках апертуры образуется синфазное поле. Геометрия параболического зеркала полностью определяется двумя параметрами – либо парой R, F (фокусное расстояние), либо R, ψ0 (угол облучения края зеркала).
Значения R, F и ψ0 |
связаны друг с другом соотношением F = |
R |
|
. |
|
2 tg(ψ0 |
2) |
||||
|
|
|
Зеркала, имеющие угол облучения ψ0 < 90о, называются длиннофокусными (F > R 2), а при ψ0 > 90о – короткофокусными.
2), а при ψ0 > 90о – короткофокусными.
4.2. Теоретические сведения
Поле излучения плоской площадки. Пусть имеется плоская площадка
Sa любой формы (рис. 4.3), в каждой точке которой заданы векторы электрического и магнитного полей:
|
|
|
|
Es |
|
x |
|
Es = exEs , |
Hs = e y Hs = e y |
Z0 |
, |
|
Es |
||
|
|
|
|
|
|
|
|
где Z0 |
– волновое сопротивление сре- |
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||||
ды, |
а |
Es , |
вообще |
говоря, |
является |
|
|
|
Ηs |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
er |
|
r |
M |
|||||||||||||||||
функцией |
точки |
|
N |
на |
поверхности |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
площадки (Es = Es (N )). В теории излу- |
y |
|
|
|
|
|
|
|
ez |
|
|
θ |
|
|
||||||||||||
чения показано, что такая площадка со- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
здает |
в |
пространстве |
электромагнитное |
|
|
|
|
Sa |
|
|
|
|
|
|
z |
|
|
|||||||||
поле. В дальней зоне это поле (поле из- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Рис. 4.3 |
|
|
|
|
|||||||||||||||
лучения) представляется в виде |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
( |
|
) |
|
e− jkr |
|
(er ); |
|
( |
|
) |
|
1 |
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z0 |
|
|
|
|
|
||||||||||||
|
|
|
Ea |
|
M |
|
= |
r |
Fa |
Ha |
|
M |
|
= |
|
er , Ea |
|
M |
|
, |
|
(4.1) |
||||
где r – расстояние от центра площадки O до точки наблюдения M ; er – орт, направленный из точки O на точку M ; k – волновое число.
Точка M находится в дальней зоне, если удовлетворяются 3 неравенства: r >> λ, r >> L, r >> L2 λ, где L – наибольший линейный размер системы (излучающей площадки). Как видно из (4.1), поле в дальней зоне представляется в виде произведения двух функций – скалярной Z0e− jkr / r , зависящей только от расстояния r =OM , и векторной Fa (er ), зависящей от направления из O на точку наблюдения M . Эта функция называется харак-
λ, где L – наибольший линейный размер системы (излучающей площадки). Как видно из (4.1), поле в дальней зоне представляется в виде произведения двух функций – скалярной Z0e− jkr / r , зависящей только от расстояния r =OM , и векторной Fa (er ), зависящей от направления из O на точку наблюдения M . Эта функция называется харак-
35

Fa max |
теристикой направленности излучающей площадки. Как |
||||
и всякий вектор, |
ее можно представить в |
виде |
|||
|
|||||
|
|
|
|
|
|
|
Fa (er )= ea Fa (er ), где орт ea указывает пространствен- |
||||
ero |
|
|
|
|
|
ную ориентацию (поляризацию) вектора Fa (er ). Соглас- |
|||||
Fa (er ) |
|
|
|
|
|
но (4.1), она совпадает с поляризацией вектора Ea . Ска- |
|||||
|
|
|
|
|
|
|
лярная характеристика направленности Fa (er ), которая |
||||
|
несет информацию об амплитудном распределении поля |
||||
|
излучения в зависимости от er , может быть записана в |
||||
Рис. 4.4 |
виде произведения |
Fa (er )= Fa max Fan (er ), где |
Fa max |
||
– значение характеристики направленности в направлении максимального излучения (орт ero на рис. 4.4). Функция Fan (er ) называется нормирован-
ной характеристикой направленности. Очевидно, Fan max
Характеристику направленности площадки можно рассчитать, если известно распределение поля Es (N ) по ее поверхности Sa . В случае синфазного распределения поля (Es (N ) = Es (N )) соответствующая формула выглядит так:
F |
(e |
r |
)= |
k |
(1+cos |
θ) |
∫ |
E |
s |
(N ) e jk(er , R)ds , |
(4.2) |
|||
|
||||||||||||||
a |
|
|
4π |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Sa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где вектор R и угол θ показаны на рис. 4.1. В данном случае направление |
||||||||||||||
максимального излучения нормально к |
Sa , т. е. ero = ez , θ = 0, а из (4.2) |
|||||||||||||
следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
= |
|
k |
∫ |
E |
s |
(N )ds . |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
a max |
|
2π |
|
|
|
|||||
|
|
|
|
|
|
|
Sa |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
Круглая площадка с центрально-симметрич- |
||||||||||
|
|
ным распределением поля. Допустим, что площадка |
||||||||||||
|
|
|
||||||||||||
ρ |
|
|
имеет форму круга (рис. 4.5), а распределение поля |
|||||||||||
|
|
Es центрально-симметричное, т. е. |
Es (N ) = Es (ρ). |
|||||||||||
|
|
|
||||||||||||
y
2R
Рис. 4.5
 θ В таком случае и характеристика направленности осе-
θ В таком случае и характеристика направленности осе-
zсимметрична, т. е. является функцией одного угла θ. После соответствующих преобразований интеграла (4.2) выражение для характеристики направленности такого раскрыва можно привести к следующему виду:
36
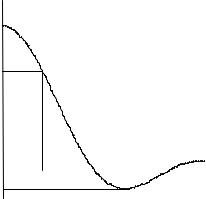
|
F (θ) |
= cos2 |
θ R E |
s |
(ρ)J |
0 |
(kρsin θ)ρdρ, |
(4.3) |
||||
|
a |
|
2 |
∫ |
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
где J0 – функция Бесселя нулевого порядка. |
|
|
|
|
||||||||
Если распределение |
поля |
однородно, |
Λ1 |
|
|
|||||||
т. е. Es (ρ)= const , то, используя (4.2) и (4.3), |
1 |
|
|
|||||||||
|
|
|
||||||||||
получим нормированную характеристику на- |
0,707 |
|
|
|||||||||
правленности в виде |
|
|
|
|
|
|
|
|
|
|
||
F |
(θ) = Λ (u)cos2 θ |
, |
|
|
(4.4) |
|
|
|
||||
an |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где u = kRsin θ |
, Λ (u) – лямбда-функция 1-го |
0 |
|
|
||||||||
1,61 |
u |
|||||||||||
|
1 |
|
|
|
|
|
|
|
–0,132 |
|||
порядка [6]. При малых значениях угла θ и |
Рис. 4.6 |
|
||||||||||
больших значениях параметра |
|
kR |
|
можно |
|
|
||||||
считать, что cos2 θ2 ≈1 и зависимость Fan (θ) при малых углах определяется в
основном первым множителем в (4.4). Вид функции Λ1 (u) показан на рис.
4.6. Как видно, это осциллирующая функция, имеющая главный и ряд боковых лепестков. Ширина главного лепестка по уровню 0,707
o |
|
o |
λ |
|
(4.5) |
2θ1min |
= 59 |
|
|
. |
|
|
2R |
||||
|
|
|
|
|
Формула (4.5) выражает фундаментальный факт: ширина главного лепестка определяется отношением радиуса площадки к длине волны. Чем больше отношение R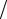 λ, тем уже лепесток, тем более остронаправленным яв-
λ, тем уже лепесток, тем более остронаправленным яв-
ляется излучение. Заметим, что ширина диаграммы (4.5), полученная для однородного распределения поля, является минимально возможной при данном отношении R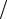 λ; именно поэтому в (4.5) фигурирует индекс min . В то же
λ; именно поэтому в (4.5) фигурирует индекс min . В то же
время при однородном распределении поля получается максимальный уровень первого бокового лепестка (0,132 или –17,6 дБ).
Если распределение поля по апертуре неоднородно (Es (ρ)≠ const ), то для расчета характеристики направленности его удобно аппроксимировать полиномом вида
Es′ (ρn )= ∑2 am (1−ρn2 )m , |
(4.6) |
m=0
где ρn =ρ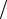 R – нормированный радиус.
R – нормированный радиус.
37
Приравнивая значения этого полинома и реального распределения Es (ρn ) в точках ρn = 0; 0,5; 1,0 , для коэффициентов am получим систему уравнений
a |
+a |
+a |
2 |
=1, a |
+0,75a +0,56a |
2 |
= E |
s |
(0, 5), a |
0 |
= E |
s |
(1), решение которой |
0 |
1 |
|
0 |
1 |
|
|
|
|
дает следующие выражения для коэффициентов:
|
a |
= E |
s |
(1), a |
= |
1 |
E |
s |
(0,5)−0,44E |
s |
(1)−0,56 , a |
2 |
=1− E |
s |
(1) |
−a . |
(4.7) |
||||
0,19 |
|||||||||||||||||||||
0 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|||||||||
|
|
Es′ (ρn ) |
|
|
|
|
|
|
При |
практических |
расчетах |
после |
|||||||||
1 |
|
|
Es (ρn ) |
нахождения коэффициентов по (4.7) целесо- |
|||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
образно рассчитать значения полинома и по- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
строить соответствующий график Es′ (ρn ) |
||||||||||
|
|
Es (0,5) |
|
|
|
|
|
|
совместно с графиком истинного распределе- |
||||||||||||
|
|
|
Es (1) |
|
|
ния Es (ρn ). Это даст возможность судить о |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
качестве аппроксимации (рис. 4.7). |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Примечание: Для повышения точности |
||||||||||
0 |
|
|
|
0,5 |
|
|
|
|
ρn |
||||||||||||
|
|
|
|
|
|
|
аппроксимации поля в ракрыве ЗА целесооб- |
||||||||||||||
|
|
|
|
Рис. 4.7 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
разно записать систему уравнений более вы- |
||||||||||||
сокого порядка чем три (порядок равен выбранному числу узлов аппроксимации), затем решить ее численно и найти поле в раскрыве по формуле (4.6) с соответствующим числом членов суммы.
Подставляя аппроксимирующий полином (4.6) в формулу (4.3), получим нормированную характеристику направленности
|
F |
|
(θ) |
= C Λ |
(u)+C Λ |
2 |
(u)+C Λ |
3 |
(u) |
cos2 θ |
, |
(4.8) |
|||||||||
|
an |
|
1 1 |
2 |
|
3 |
|
|
|
2 |
|
|
|
||||||||
где коэффициенты Cn равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
C1 = |
|
6a0 |
|
|
, C2 = |
3a1 |
|
, |
C3 = |
|
2a2 |
|
. |
||||||||
6a +3a +2a |
2 |
6a +3a +2a |
2 |
6a +3a +2a |
2 |
||||||||||||||||
0 |
|
1 |
|
|
0 |
|
1 |
|
|
|
|
|
0 |
1 |
|
||||||
В (4.8) входят лямбда-функции n -го порядка Λn (u). Значения этих |
|||||||||||||||||||||
функций можно вычислить по формуле Λn (u) = |
|
n! |
|
|
Jn (u), где |
Jn (u) – |
|||||||||||||||
(u 2)n |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
функция Бесселя n-го порядка [6] .
По рассчитанной характеристике направленности Fan (θ) можно найти ширину ее главного лепестка 2θ10 , которая окажется больше минимально возможной, найденной по формуле (4.5). Отношение 2θ10  2θ1min0 называется
2θ1min0 называется
38
коэффициентом расширения луча (КРЛ). Эта величина показывает, во сколько раз ширина основного лепестка (луча) при данном распределении Es больше, чем при однородном распределении, но при том же значении R λ. Обычно КРЛ равен 1,1…1,3.
λ. Обычно КРЛ равен 1,1…1,3.
По рассчитанной характеристике Fan (θ) можно также найти уровень
первого бокового лепестка (УБЛ). При распределении поля, спадающем от центра к краю апертуры, УБЛ оказывается меньше, нежели при однородном распределении (0,132). При этом, чем быстрее спадает поле, тем меньше УБЛ.
Коэффициент направленного действия и апертурный КИП площад-
ки. Важнейшим параметром, характеризующим направленность любой антенны, является коэффициент направленного действия (КНД). По одному из нескольких эквивалентных определений КНД есть отношение плотности потока мощности на единицу телесного угла в направлении максимального излучения к средней по полному телесному углу 4π плотности потока мощности той же антенны.
Свяжем это определение с характеристикой направленности. Известно, что величина Fa2 (er ) 2 есть плотность потока мощности на единицу телесного угла в направлении орта er . Следовательно, в направлении максимального излучения она равна Fa2max
2 есть плотность потока мощности на единицу телесного угла в направлении орта er . Следовательно, в направлении максимального излучения она равна Fa2max  2. Чтобы получить среднюю по телесному углу 4π плотность потока мощности, нужно полную мощность Pa , излучаемую площадкой, разделить на 4π. Тогда, в соответствии с определением, КНД площадки
2. Чтобы получить среднюю по телесному углу 4π плотность потока мощности, нужно полную мощность Pa , излучаемую площадкой, разделить на 4π. Тогда, в соответствии с определением, КНД площадки
|
1 F2 |
|
|||
D = |
2 a max |
. |
(4.9) |
||
|
|||||
a |
1 |
P |
|
||
|
|
4π |
|
||
|
|
a |
|
||
Величина, стоящая в числителе (4.9):
1 |
F |
2 |
= |
1 |
|
2k 2 |
1 |
|
∫ |
E |
|
(N ) dS |
2 |
. |
|
|
|
|
|
|
|
|
s |
|
|||||||
2 |
|
2 |
Ζ |
|
|
||||||||||
a max |
|
|
4π |
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Sa |
|
|
|
|
|
||
Значение мощности Pa , входящее в знаменатель (4.9), можно найти ч е- рез Es (N ) как поток вектора Пойнтинга через площадку Sa :
P = |
1 |
∫ |
E2 |
(N ) dS . |
|
||||
a |
2Ζ0 |
s |
|
|
|
Sa |
|
|
39
Тогда выражение (4.9) для КНД приводится к виду |
|
|||||||||||
D |
|
= 4π |
Sa |
g , |
(4.10) |
|||||||
|
|
|
|
|||||||||
a |
|
|
|
λ2 |
|
|||||||
|
|
|
|
|
|
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
Es dS |
|
2 |
|
|
|||||
|
|
|
|
|||||||||
g = |
|
Sa |
|
|
|
|
|
|
. |
(4.11) |
||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
Sa ∫ |
|
Es |
|
2 dS |
|
||||||
|
|
|
|
|||||||||
Sa
Как видно из (4.10), основным фактором, определяющим КНД синфазной апертуры, является отношение ее геометрической площади Sa к квадрату длины волны. С ростом этого отношения растет и КНД, что вполне согласуется с полученным ранее выводом о возрастании направленности излучения с ростом R λ.
λ.
Коэффициент g , входящий множителем в (4.10), учитывает влияние на КНД формы распределения поля Es по площадке. Он называется апертурным коэффициентом использования площади (апертурный КИП). Из формулы (4.11) видно, что максимально возможное значение g , равное 1, получается при равномерном распределении. При неравномерном распределении g < 1. Обычно g = 0,6...0,9. Поскольку апертурный КИП зависит только от
распределения поля Es , его можно вычислить, |
зная коэффициенты аппрок- |
|||||||||||||||
симирующего полинома (4.6): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
+ |
1 |
a1 + |
1 |
a2 |
2 |
|
|
|
|
|
|
|
|
|
|
a0 |
2 |
3 |
|
|
|
|
|
|
|
|||
g = |
|
|
|
|
|
|
|
|
|
|
|
|
. |
(4.12) |
||
a2 |
+ 1 a2 |
+ 1 a2 |
+a a |
+ |
2 a a |
2 |
+ 1 a a |
|||||||||
0 |
3 |
1 |
5 |
2 |
|
0 1 |
|
3 |
0 |
|
2 |
1 2 |
|
|
||
Распределение поля в апертуре параболического зеркала. Если диа- |
||||||||||||||||
грамма направленности облучателя F0 (ψ) осесимметрична, т. е. зависит |
||||||||||||||||
только от угла ψ, то поле Es |
в апертуре будет центрально-симметричным: |
|||||||||||||||
Es = Es (ρ). Функция Es (ρ) |
зависит от диаграммы облучателя F0 (ψ). Связь |
|||||||||||||||
между этими двумя функциями можно установить с помощью условия энергетического баланса (рис. 4.2) в лучевых трубках до и после отражения от зеркала. Очевидно, в конической трубке с телесным углом dΩ заключена та же мощность, что и в цилиндрической трубке с площадью dS (см. рис. 4.2).
40
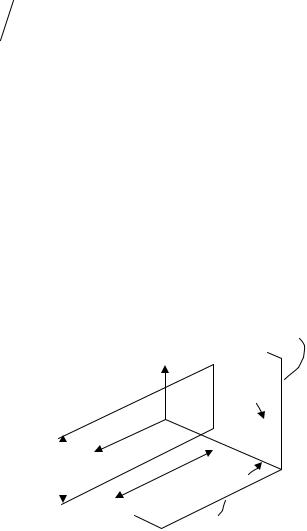
Расчет показывает, что распределение поля Es в функции нормированного радиуса ρn выражается через ДН облучателя следующим образом:
E |
s |
(ρ |
n |
)= F |
(ψ)cos2 ψ . |
(4.13) |
|
|
0 |
2 |
|
||
|
|
|
|
|
|
|
Постоянный множитель в (4.13) опущен, а нормированный радиус ρn и |
||||||
угол ψ связаны при этом жестким соотношением |
|
|||||
|
|
ρn |
= tg ψ |
tg ψ0 . |
(4.14) |
|
|
|
|
|
2 |
2 |
|
Расчет Es (ρn ) по известной ДН F0 (ψ) выполняется так. Задают после- |
||||||
довательностью углов ψ = 0 ψ0. Для каждого из них, зная |
F0 (ψ), находят |
|||||
по (4.14) значения ρn , а по (4.13) – |
соответствующие значения Es . По |
|||||
найденной функции Es (ρn ) |
|
можно рассчитать нормированную характери- |
||||
стику направленности апертуры зеркала. Для этого нужно найти коэффиц и- енты аппроксимирующего полинома и проверить качество аппроксимации. Далее рассчитываются коэффициенты Cn и нормированная ДН по формуле
(4.8). Располагая этой ДН, можно найти ширину главного лепестка 2θ10 и КРЛ. Наконец, находятся апертурный КИП g и КНД.
Облучатели зеркальных антенн. Од- |
|
|
|
|
|
|
Е-плоскость |
||
ним из наиболее распространенных облуча- |
|
|
|
|
|||||
телей зеркальных антенн являются рупора с |
|
|
|
||||||
|
|
|
Es |
||||||
прямоугольным раскрывом, возбуждаемые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямоугольным волноводом (рис. 4.8). При |
|
|
|
|
|
|
|
Ψ |
|
|
|
|
|
|
|
|
|||
их использовании возникает вопрос об осе- |
|
|
|
|
|
|
|
|
|
bp |
|
|
|
|
|
|
|||
|
ap |
|
|
|
|||||
вой симметрии их диаграммы направленно- |
Hs |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти, которая необходима для создания в |
|
|
|
|
|
|
Н-плоскость |
||
|
|
|
|
|
|
||||
апертуре зеркала осесимметричного распре- |
|
|
|
|
|
|
|||
|
|
|
Рис. 4.8 |
||||||
деления поля. Повлиять на ДН рупора мож- |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
но только одним способом – выбором размеров апертуры ap и bp . Однако
можно убедиться, что ни одна из комбинаций этих размеров не приводит к полностью осесимметричной ДН. Это видно хотя бы из того, что в плоскостях E и H ДН рупора описываются разными функциями угла ψ. В Е- плоскости это выражение имеет вид
41
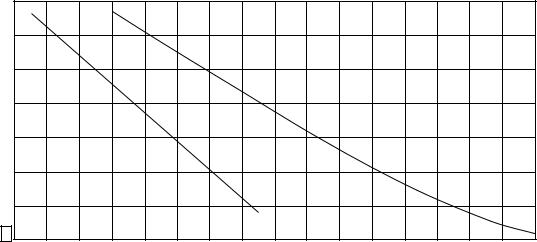
|
|
|
|
|
|
kb |
|
|
|
|
|
||||||
|
(ψ)= cos2 ψ |
|
|
sin |
|
|
p |
sin ψ |
|
||||||||
|
|
|
|
|
|||||||||||||
F |
|
|
|
|
|
2 |
|
|
|
|
, |
(4.15) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0E |
2 |
|
|
|
|
kbp |
sin ψ |
|
|
|
|
||||||
а в H-плоскости, соответственно, |
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
kap |
|
|
|
||||||||
|
(ψ)= cos2 ψ |
|
cos |
|
|
|
|
|
sin |
ψ |
|
||||||
|
2 |
|
|
|
|||||||||||||
F |
|
|
|
|
|
|
|
|
|
. |
(4.16) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
0H |
2 |
|
|
|
kap |
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
− |
|
|
|
|
sin ψ |
|
||||||||
|
|
|
|
π |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому возможно создание лишь приближенно осесимметричной ДН. Потребуем, чтобы значения ДН в обеих плоскостях совпали при ψ = ψ0 . Тогда процедура расчета размеров рупора может быть следующей. Известны
угол ψ0 и уровень облучения края зеркала |
F0 = F0E (ψ0 )= F0H (ψ0 ). Из |
|||||||||||||||||||
(4.15) и (4.16) вытекают тогда следующие равенства: |
|
|
|
|
||||||||||||||||
|
|
f1 = |
sin |
ν |
= |
F0 |
, |
f2 |
= |
|
cos ν |
= |
F0 |
, |
(4.17) |
|||||
|
|
ν |
|
cos |
2 ψ0 |
|
2 |
2 |
cos |
2 ψ0 |
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
− |
|
|
ν |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
||
где ν = |
k bp |
sin ψ0 |
для функции f1 |
и ν = |
k ap |
sin ψ0 |
для функции f2. Разре- |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
шить равенства (4.17) относительно ν можно, имея графики функций, стоящих в равенствах слева. Эти графики приведены на рис. 4.9. Зная ν, а также ψ0 и λ, легко найти ap и bp .
f1, f2 |
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
0,3 |
|
|
f1 |
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
0 |
1,8 |
2,2 |
2,6 |
3 |
3,4 |
3,8 |
4,2 |
ν |
1,4 |
||||||||
0,4 |
|
|
|
|
f2 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.9
42
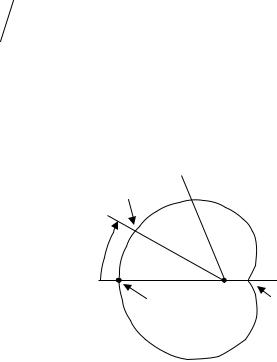
Если размеры рупора выбраны из условия F0E (ψ0 )= F0H (ψ0 ), то диаграмму направленности F0 (ψ) можно далее считать приближенно осесим-
метричной, а для ее аналитического представления использовать одну из формул (4.15) или (4.16). В дальнейшем остановимся на (4.15).
Переливание мощности через край зеркала. Эффективность облуча-
теля. В зеркальных антеннах с облучателями традиционных типов (рупор, полуволновый вибратор с рефлектором и т. п.) не вся мощность облучателя ΡΣ
перехватывается зеркалом. Действительно, доля мощности ΡΣ, соответствующая той части ДН облучателя, которая выходит за пределы угла 2ψ0 на рис. 4.6,
переливается через край зеркала и не попадает в его апертуру. Это обстоятельство снижает КНД антенны в целом, который получается меньше КНД апертуры Da . По определению, КНД антенны представляется отношением типа (4.9)
|
|
D = |
1 F2 |
1 |
P , |
(4.18) |
|
|
4π |
||||
|
1 F2 |
|
2 max |
Σ |
|
|
где |
– плотность потока мощности антенны на единицу телесного угла |
|||||
|
2 max |
|
|
|
|
|
в направлении ее максимального излучения. Строго говоря, в этом направлении складывается 2 поля – поле излучения апертуры и поле заднего излучения облучателя (рис. 4.10). Однако последнее обычно незначительно и им
можно пренебречь. Следовательно, в (4.18) можно |
|
F (Ψ) |
Ψ = Ψ0 |
||||
сделать замену 1 F2 |
|
|
1 F2 |
|
0 |
|
|
|
на |
. Деля и умн о- |
|
|
|
||
2 max |
|
2 a max |
|
|
|
|
|
жая (4.18) на Pa , получим |
|
|
Ψ |
|
|
||
|
|
|
|
|
|||
|
D = Daα1, |
(4.19) |
|
F0(0) |
F (π) |
||
где α1 – отношение мощности, падающей на зер- |
|
|
0 |
||||
|
|
|
|||||
кало и проходящей затем апертуру ( Pa ), к полной |
|
|
|
||||
мощности облучателя (PΣ ). Это отношение и уч и- |
|
Рис. 4.10 |
|||||
тывает факт переливания мощности за край зеркала и называется эффективностью облучателя. Эффективность облучателя можно рассчитать по известной ДН облучателя и углу облучения края зеркала:
|
|
|
ψ0 |
F2 (ψ)sin ψ dψ |
|
||
|
|
|
∫ |
|
|||
|
P |
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
α = |
a |
= |
|
|
. |
(4.20) |
|
|
|
|
|
||||
1 |
PΣ |
|
πF2 |
(ψ)sin ψ dψ |
|
||
|
|
|
|||||
|
|
|
∫ |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
43
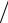
Подставляя (4.10) в (4.19), получим |
|
||
D = 4π |
Sa gα1 |
. |
(4.21) |
|
|||
|
λ2 |
|
|
Максимизация КНД антенны. Обратим внимание на то, что при задан- |
|||
ном угле облучения края зеркала ψ0 значения g и α1 |
изменяются в зависи- |
||
мости от выбора ДН облучателя F0 (ψ). При этом, если сужать эту ДН, то α1 растет (см. (4.20)), а g падает, ибо при этом увеличивается неравномерность распределения поля Es в апертуре. Следовательно, произведение gα1 при определенной ширине диаграммы F0 (ψ) должно иметь максимум. При этом
максимизируется и КНД (площадь апертуры и длина волны фиксированы). Выражая апертурный КИП через ДН облучателя, получим
|
|
|
ψ0 |
|
|
2 |
|
|
|
||
|
|
|
|
∫ |
F0 (ψ) tg ψ dψ |
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
|
g = 2 ctg |
2 ψ0 0 |
|
|
|
|
. |
|
(4.22) |
|||
2 |
|
ψ0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∫ |
F2 (ψ) sin ψ dψ |
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Составим произведение (4.20) и (4.22). Тогда |
|
|
|
|
|||||||
|
|
|
|
ψ0 |
F0 (ψ) tg |
ψ |
2 |
|
|||
|
|
|
|
|
∫ |
dψ |
|
|
|
||
|
|
|
|
2 |
|
|
|
||||
|
2 ctg2 ψ0 |
|
|
|
|
|
|
|
|||
gα = |
0 |
|
|
|
. |
(4.23) |
|||||
|
|
|
|
||||||||
1 |
|
2 |
|
π |
F2 (ψ) sin ψ dψ |
|
|
|
|||
|
|
|
|
|
∫ |
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Если в качестве облучателя использовать рупор с приближенно осесимметричной ДН типа (4.15), то выражение (4.23) можно свести к следующему:
|
|
|
|
|
|
|
|
kb ψ |
0 |
|
|
|||||
|
|
ap |
|
ctg2 ψ0 |
sin4 |
|
|
p |
|
|
|
|||||
|
|
|
|
4 |
|
|
|
|||||||||
gα = 0,258 |
ψ2 |
|
|
|
|
|
|
|
. |
(4.24) |
||||||
bp |
|
|
|
|
|
|
2 |
|
||||||||
1 |
|
0 |
2 |
|
kb ψ |
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Считая, что угол ψ0 |
и отношение ap bp |
известны, видим, что gα1 яв- |
||||||||||||||
ляется функцией параметра ξ = kbpψ0  4, входящего в последний множитель
4, входящего в последний множитель
в (4.24). Можно показать, что этот множитель при ξ = 1,165 имеет максимальное значение, равное 0,525. Отсюда вытекает следующая рекомендация:
44

для того чтобы зеркальная антенна с рупорным облучателем имела максимально возможный КНД, произведение kbp следует выбирать равным
(kbp ) |
opt |
= |
4,66 . |
(4.25) |
|
|
|
ψ |
|
||
|
|
|
|
0 |
|
Таким образом, каждому углу |
ψ0 |
соответствует определенное опти- |
|||
мальное значение kbp . Расчетная процедура, позволяющая найти оптималь-
ный рупорный облучатель, иллюстрируется следующим примером.
Задача. Угол облучения края зеркала ψ0 = 70º = 1,22 рад. Определить размеры рупора ap и bp , для которых КНД антенны максимален (максимально произведение gα1) при λ= 30 мм.
Решение. 1. Из (4.25) находим kbp = 3,82. 2. Зная λ и kbp , находим bp = = 18,24 мм. 3. Размер ap ищем, исходя из условия осевой симметрии ДН.
Сначала |
находим уровень облучения края зеркала, |
используя (4.15) |
при |
||||||||||||
ψ = ψ |
0 |
: |
|
F = 0,366. Далее, используя (4.16), получим |
cos ν |
|
= 0,545, где |
||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
2 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
1− |
|
ν |
|
|
||
|
|
|
|
|
|
|
|
|
π |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ν = |
kap |
sin ψ0 . Зная правую часть этого равенства, по графику на рис. |
4.9 |
||||||||||||
2 |
|
|
|||||||||||||
|
|
|
|
|
kap |
|
|
|
|
|
|
|
|||
находим |
ν = 2,4 . Наконец, из выражения ν = |
sin ψ0 находим ap = 24,4 |
|||||||||||||
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мм. Таким образом, ap bp = 1,34. 4. Значение gα1 |
находим по (4.24), учиты- |
||||||||||||||
вая, что последний множитель равен 0,525: gα1= 0,553.
Как видно, произведение gα1 получилось заметно меньше единицы. Поэтому в стремлении повысить КНД зеркальных антенн разрабатывались облучатели, обладающие параметром gα1, близким к единице. Чтобы этого добиться, нужно сформировать такую ДН облучателя, при которой распределение поля в апертуре было бы однородным (тогда g = 1) и отсутствовало бы переливание мощности за край зеркала (тогда α1= 1). Этим требованиям удовлетворяет гипотетический облучатель с диаграммой вида
|
|
1 |
при |
ψ = 0 ψ0 |
, |
F0 |
|
|
|||
|
|||||
(ψ)= cos2 ψ 2 |
|
|
(4.26) |
||
|
|
0 |
при |
ψ > ψ0 . |
|
|
|
|
|||
45

Точная реализация ДН (4.26) невозможна, однако существуют облучатели с ДН, близкими к (4.26).
Снижение КНД вследствие затенения апертуры. Облучатель, имею-
щий некоторую площадь раскрыва SΤ , частично затеняет апертуру зеркала. Это приводит к уменьшению КНД апертуры и антенны в целом и учитывается множителем α2 , который вводится в выражение для КНД и носит назв а- ние прозрачности апертуры. Его приближенно можно рассчитать по формуле
|
|
|
SΤ 2 |
|
||||
α2 |
≈ |
1− |
|
|
. Таким образом, окончательное выражение для КНД антенны |
|||
|
||||||||
|
|
|
Sa |
|
|
|
|
|
с учетом (4.21) будет следующим: |
|
|||||||
|
|
|
|
|
D = 4π |
Sa gα1α2 |
. |
(4.27) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
λ2 |
|
|
Кроссполяризация. При рассмотрении излучения апертуры предполагалось, что вектор Es во всех ее точках поляризован вдоль орта ex , как показано на рис. 4.11. Однако в реальных зеркальных антеннах процессы, происходящие при отражении поля излучателя от зеркала, таковы, что в апертуре появляется помимо основной (вертикальной) составляющей поля Es перпен-
xдикулярная ей горизонтальная составляющая. Эта так называемая кроссполяризационная со-
|
|
|
|
|||
|
|
Ex |
ставляющая имеет в разных квадрантах зеркала |
|||
Ey |
|
|
|
|
|
различную полярность (рис. 4.11). Уровень кросс- |
|
|
|
|
|
|
|
|
|
|
|
|
|
поляризационной составляющей зависит от угла |
y |
|
|
|
|
|
облучения края зеркала – чем меньше этот угол, |
|
|
|||||
|
|
|
|
|
|
тем ниже уровень кроссполяризации. Этот уро- |
|
|
|
|
|
|
|
|
|
|
|
|
|
вень также существенно зависит от типа облуча- |
Рис.4.11 |
теля. В частности, известно, что при облучателе |
|||||
типа диполя Герца уровень кроссполяризации |
||||||
достаточно высок. В то же время при облучателе в виде элемента Гюйгенса кроссполяризация практически отсутствует. Поскольку рупорные облучатели в определенном смысле близки к элементу Гюйгенса, их применение с этой точки зрения более предпочтительно. Обычно доля кроссполяризационного излучения по сравнению с излучением по основной составляющей составляет единицы процента по мощности.
46
