3.Основные расчетные формулы. Рассчитанные и экспериментально снятые ДН спиральных антенн в полярной или декартовой системе координат, представленные на одном рисунке.

4.Результаты расчетов ширины главного лепестка и КНД СА по формулам (2.6), (2.7) (КНД рассчитать в децибеллах и относительных единицах).

5.Выводы по работе.

3.ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ РУПОРНОЙ АНТЕННЫ

3.1. Теоретические сведения

Все параметры, характеризующие антенны, можно разделить на 2 группы. К первой группе следует отнести параметры, характеризующие антенну как элемент цепи приёмопередающего тракта. Так, передающая антенна может рассматриваться как нагрузка для выходного каскада передатчика и описываться соответствующими параметрами теории цепей: входным сопротивлением, коэффициентом отражения и т. д. Приёмная антенна с этой точки зрения может рассматриваться как обладающий определённым внутренним сопротивлением источник напряжения.

Ко второй группе следует отнести параметры, характеризующие антенну как элемент, преобразующий энергию, поступающую по фидерному тракту, в энергию электромагнитных волн, распространяющихся в пространстве, и распределяющий в пространстве интенсивность полей этих волн (передающая антенна). Приёмная же антенна может рассматриваться как устройство, преобразующее энергию пространственных электромагнитных волн (с учётом направления их прихода) в энергию волн фидера. В эту группу включены такие параметры и характеристики, как коэффициент полезного действия (КПД), диаграмма направленности (ДН), коэффициент направленного действия (КНД), коэффициент усиления (КУ) и др.

Как правило, в реальных антеннах всегда имеются необратимые потери энергии, связанные, в основном, с конечным значением проводимости металла и неидеальностью диэлектрика. Из-за этого мощность P1 , преобразованная

антенной, всегда будет меньше мощности P0 , поступающей в антенну. КПД антенны η характеризует эффективность преобразования энергии и определяется соотношением η= P1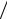P0 .

17

Другие параметры второй группы, упомянутые здесь, определяются для дальней зоны антенны.

В дальней зоне (зоне излучения) электромагнитное поле, созданное антенной, представляет собой поперечную волну со сферическим волновым фронтом. Дальняя зона формируется при удалении от антенны на расстояние R, удовлетворяющее следующим условиям:

где L – максимальный линейный размер апертуры антенны; λ – рабочая длина волны.

ДН описывает пространственное распределение амплитуды поля излучения антенны в дальней зоне.

КНД антенны D характеризует степень концентрации антенного излучения в заданном направлении (обычно в направлении максимального излучения). По определению, значение коэффициента направленного действия показывает, во сколько раз плотность потока мощности излучения рассматриваемой антенны в заданном направлении больше плотности потока мощности, создаваемого изотропным (ненаправленным) излучателем при условии равенства полных мощностей, излучаемых рассматриваемой и изотропной антеннами. Как показано в теории антенн, КНД апертурной антенны с синфазным раскрывом можно найти по формуле

где Sэф = gS – эффективная площадь апертуры; S – её геометрическая пло-

щадь; g – апертурный коэффициент использования поверхности раскрыва (КИП), связанный с распределением по апертуре касательной составляющей поля ES следующим соотношением:

∫ ES dS 2

g = SS∫ ES 2 dS .

S

КУ антенны G показывает, во сколько раз плотность потока мощности излучения антенны в заданном направлении больше плотности потока мощности, создаваемого идеальным (без потерь) изотропным излучателем при условии равенства мощностей, подводимых к рассматриваемой и изотропной

18

антеннам. Из определения видно, что КУ антенны характеризует степень концентрации излучения в пространстве с учётом потерь в антенне. Между КУ и КНД существует связь: G = Dη.

На практике нередко значения КНД или КУ определяют в децибелах (дБ). Коэффициент усиления G1 (в дБ) связан с величиной G, выраженной в

относительных единицах, равенством G1 = 10 lg G .

В данной работе производятся измерения коэффициентов усиления рупорных антенн.

Рупорная антенна состоит из отрезка волновода постоянного сечения размером a ×b и собственно рупора, представляющего собой волновод с плавно изменяющимся сечением, с размерами раскрыва aр ×bр. На практике

применяются 2 типа прямоугольных рупоров – секториальные и пирамидальные. Секториальными называются рупоры, у которых расширяется только одна пара стенок. В зависимости от того, в какой плоскости происходит расширение, различают Е-плоскостные (aр = a , bр > b) и Н-плоскостные

( aр > a , bр = b ) рупоры. Пирамидальными называются рупоры, расширяю-

щиеся как в плоскости вектора Е, так и в плоскости вектора Н. Характеристики излучения рупорной антенны определяются структурой

поля в ее раскрыве. В общем случае ДН F (θ, ϕ) плоской прямоугольной излучающей апертуры размером aр ×bр описывается выражением

Функции FE (θ, ϕ) и FH (θ, ϕ) определяются амплитудно-фазовым рас-

пределением поля в раскрыве апертуры в плоскостях векторов E и H соответственно.

Для рупорной антенны с достаточной точностью можно считать, что амплитуда поля в раскрыве распределена так же, как и амплитуда поля основ-

В случае синфазного раскрыва (ψ(x, y) = const) функции FE (θ, ϕ) и FH (θ, ϕ) будут определяться формулами

19

нии продолжений граней рупора. Если приближенно считать, что цилиндрическая волна распространяется между параллельными широкими стенками рупора с волновым числом k, то набег фазы в то чке апертуры с координатой x равен kr(x), а в центре апертуры – kLH ( LH – длина Н-плоскостного рупора). Таким образом, разность фаз в точках с координатами x и 0

ψH (x) = k LH − r (x) = k LH −LH 2 + x2 .

Предполагая, что угол раскрыва рупора мал, заменим корень в этом в ы- ражении первыми двумя членами разложения Маклорена:

Отсюда видно, что расфазировка возрастает от центра к краю апертуры приблизительно по квадратичному закону и максимальное её значение – фа-

зовая ошибка ΨH max – достигается на краю раскрыва:

Диаграмма направленности Н-плоскостного рупора с фазовым распределением (3.6) описывается формулой (3.3), где FE (θ,ϕ) определяется вы-

20

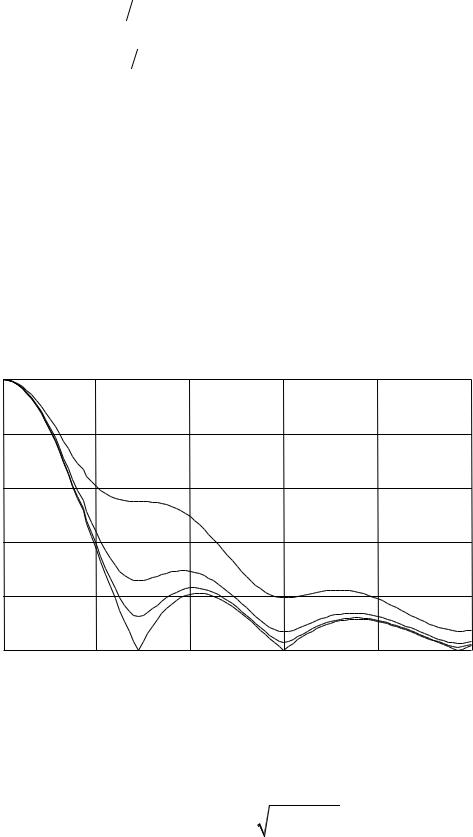
ражением (3.4), а FH (θ,ϕ) при условии малости угла раскрыва рупора даётся интегралом

который может быть представлен линейной комбинацией специальных функций – интегралов Френеля [6].

На рис. 3.2 представлены диаграммы направленностиFH (θ) в плоскости Н (ϕ = 0) для рупора с размером aр = 4λ при различных значениях нормированной длины рупора LH 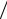λ и, согласно (3.7), максимальной фазовой ошибки

ΨH max . Кривая 2 соответствует значению LH λ = 20, кривая 3 – LH λ = 10, 4 – LH 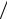λ = 5. Для сравнения там же приведена диаграмма направленности син-

фазного раскрыва (кривая1). Как видно из графиков, наличие в раскрыве квадратичной фазовой ошибки (3.6) приводит к деформации ДН: заплывают нули, увеличивается уровень бокового излучения, расширяется основной лепесток.

FH (θ)

Рис. 3.2

Аналогичным образом влияет на диаграмму направленности в плоскости Е (ϕ = ±π2 ) для Е-плоскостного рупора фазовая ошибка ψE (y), определяемая выражением

21

В этом случае для расчёта диаграммы направленности рупора в формулу (3.3) следует подставить FH (θ, ϕ) из (3.5), а FE (θ, ϕ) будет выражаться интегралом

также сводимым к линейной комбинации интегралов Френеля.

Влияние фазовой ошибки в раскрыве рупорной антенны проявляется в том, что значение КИП зависит от относительных размеров рупора aр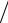λ,

bр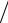λ, LH 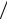λ , LE λ. Таким образом, КНД Н-плоскостного рупора будет определяться выражением

DH = 4π aλрb2р gH (aр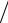λ, LH λ),

где gH – функция, определяющая зависимость КИП (g) от комбинации параметров aр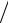λ и LH 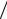λ . Пользуясь общим выражением для КИП, нетрудно показать, что

Удобнее, однако, иметь дело с приведённым КНД DH λ , поскольку bр

при варьировании размеров Н-плоскостного рупора отношение bр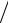λ остаёт-

ся неизменным. Очевидно, приведённый КНД Н-плоскостного рупора будет определяться выражением

DH bλр = 4π aλр gH aλр , LλH .

Аналогичным образом можно найти и приведённый КНД для Е-плос- костного рупора:

DE aλр = 4πbλр gE bλр , LλE ,

где

22

E-плоскостных рупоров соответственно. Параметры LH 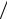λ на рис. 3.3 и LE λ

на рис. 3.4 принимают значения от 2 (кривая 1) до 6 (кривая 11) с шагом 0,4. Как видно из этих графиков, с увеличением относительных размеров раскрыва рупора (aр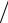λ или bрλ) при его неизменной длине Lλ КНД сначала возрас-

тает, так как увеличиваются размеры излучающей поверхности, которая остаётся практически синфазной (сдвиг фаз ΨH ,E max мал). При этом ДН стано-

вится уже. При дальнейшем увеличении размеров раскрыва заметно растут фазовые искажения, что приводит к снижению КНД и расширению ДН.

DНλ/bp

35

1

10

Рис. 3.3

Допустимое значение максимальной фазовой ошибки ΨH ,E max опреде-

ляется условием получения наибольшего КНД при заданной относительной длине Lλ рупора. Установлено, что в случае Е-плоскостного рупора макси-

мальный КНД получается при выполнении соотношения LE opt = bр2 2λ, что

23

и ΨH max = 3π4 .

Увеличение допустимого сдвига фаз в апертуре Н-плоскостного рупора по сравнению с Е-плоскостным объясняется спаданием амплитуды возбуждающего поля к краям этого рупора.

Следует отметить, что «оптимальность» здесь понимается в смысле получения наибольшего значения КНД при заданной длине рупора LE или LH .

Коэффициент направленного действия оптимального Е- или Н-плоско- стного рупора

Dopt = 0,64 4λπ2S .

КНД пирамидального рупора с размерами раскрыва aрλ и bрλ можно рассчитать по формуле

24