
- •1.1. Введение, теоретические сведения
- •1.2. Экспериментальная установка
- •1.3. Лабораторный эксперимент
- •1.4. Контрольные вопросы
- •1.5. Содержание отчета
- •2. ИССЛЕДОВАНИЕ СПИРАЛЬНОЙ АНТЕННЫ
- •2.1. Введение. Теоретические сведения
- •2.2. Экспериментальная установка
- •2.3. Проведение измерений
- •2.4. Контрольные вопросы
- •2.5. Содержание отчета
- •3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ РУПОРНОЙ АНТЕННЫ
- •3.1. Теоретические сведения
- •3.2. Методика измерения коэффициента усиления антенны
- •3.3. Лабораторный макет
- •3.4. Проведение измерений
- •3.5. Обработка результатов измерений
- •3.6. Контрольные вопросы
- •3.7. Содержание отчёта
- •4. ИССЛЕДОВАНИЕ ЗЕРКАЛЬНОЙ АНТЕННЫ
- •4.1. Введение. Принцип действия зеркальной антенны
- •4.2. Теоретические сведения
- •4.2. Экспериментальная установка
- •4.3. Эксперимент
- •4.4. Обработка результатов эксперимента.
- •4.5. Контрольные вопросы
- •4.6. Содержание отчета
- •5. ВЛИЯНИЕ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ НА ДИАГРАММЫ НАПРАВЛЕННОСТИ АНТЕНН
- •5.1. Идея метода зеркальных изображений
- •5.2. Применение метода зеркальных изображений к антеннам, размещенным над проводящей плоскостью
- •5.3. Обобщение на антенны с произвольно поляризованным излучением
- •5.4. Интерференция полей антенны и ее зеркального изображения
- •5.5. Частные случаи
- •5.6. Интерференционные множители
- •5.7. Экспериментальная установка
- •5.8. Проведение измерений
- •5.9. Обработка результатов и теоретические расчеты
- •5.10. Контрольные вопросы
- •5.11. Содержание отчета
- •6. ИССЛЕДОВАНИЕ МНОГОЭЛЕМЕНТНОЙ АНТЕННОЙ РЕШЕТКИ «ВОЛНОВОЙ КАНАЛ»
- •6.1. Общие сведения
- •6.2. Математическое описание вибраторных антенных решеток
- •6.2.1. Система связанных интегральных уравнений для многоэлементной антенной решетки ВК
- •6.2.2. Решение системы связанных ИУ
- •6.2.3. Метод наведенных ЭДС
- •6.3. Описание лабораторного макета
- •6.4. Задание и указания к выполнению работы
- •6.4.1. Измерение КСВ ВК1 и ВК2 в полосе частот 2…3 ГГц
- •6.4.2. Экспериментальное исследование ДН ВК1 в Е- и в Н-плоскостях на заданных дискретных частотах из интервала 2.35…2.45 ГГц
- •6.4.3. Расчет основных характеристик ВК на основе электродинамического моделирования в специализированных пакетах
- •6.5. Требования к содержанию отчета
- •6.6. Контрольные вопросы
- •7. ИССЛЕДОВАНИЕ МИКРОПОЛОСКОВОЙ АНТЕННОЙ РЕШЕТКИ
- •7.1. Общие сведения
- •7.2. Математическое описание МПА
- •7.3. Лабораторный макет
- •7.4. Программа работ
- •7.4.1. Измерение КСВ МПАР в полосе частот 3.0…4.0 ГГц
- •7.4.2. Экспериментальное исследование ДН МПАР
- •7.4.3. Расчет ДН МПАР на основе приближенной модели
- •7.4.4. Измерение отношения «вперед/назад»
- •7.4.5. Измерение ДН по кросс поляризации (выполняется по указанию преподавателя)
- •7.4.6. Расчет характеристик МПАР на основе моделирования в специализированном пакете
- •7.5. Требования к содержанию отчета
- •7.6. Контрольные вопросы
- •Список литературы
- •Оглавление
14.Как будут выглядеть уравнения (1.1), если вход пассивного вибратора замкнуть накоротко?
15.Опираясь на выражение (1.2), выведите выражения (1.3) и (1.4).
16.Что понимают под входным сопротивлением антенны, состоящей из активного и пассивного вибраторов?
17.Опираясь на выражение (1.5), выведите выражения (1.6).
18.От каких параметров зависит системный множитель ДН рассматриваемой антенны?
19.Покажите на формулах, что характеристику направленности системы можно изменять, перестраивая сопротивление Xн.
20.Что такое отношение «вперед/назад»?
21.В каких случаях можно говорить, что пассивный вибратор работает как идеальный рефлектор или директор? Чему в этих случаяхравно отношение q?
1.5. Содержание отчета
Отчет должен содержать:
1.Структурную схему установки с указанием всех основных узлов приемного и передающего тракта;
2.Результаты эксперимента в виде зависимостей уровня поля от длины шлейфа, ДН в режиме рефлектора и директора с указанием расстояния между элементами и выбранных оптимальных значений длин шлейфа;
3.Расчетные данные:
–график отношения вперед/назад (1.9), как функция длины шлейфа. Здесь следует отметить, что коэффициент m (отношение токов в вибраторах) зависит от Хн, который в свою очередь определяется длинной шлейфа lш.
–расчетные ДН в виде графиков (1.8).
4.Выводы по работе.
2.ИССЛЕДОВАНИЕ СПИРАЛЬНОЙ АНТЕННЫ
2.1. Введение. Теоретические сведения
Спиральные антенны (СА) широко используются в качестве самостоятельных излучателей или в составе небольших антенных решеток как широкополосные излучатели круговой поляризации, работающие в режиме осевого излучения. Чаще всего СА представляет собой спиральный проводник ограниченной длины (несколько длин волн), намотанный на диэлектрический каркас, один конец проводника СА подсоединен к внутренней жиле возбуж-
10

дающего коаксиального кабеля, другой |
|
|
оставлен свободным. Внешняя оплетка |
|
|
кабеля присоединяется к проводящему |
|
|
экрану (основанию) (рис. 2.1). Наиболее |
|
|
распространен режим работы цилиндри- |
|
|
ческой СА, при котором диаметр ци- |
|
|
линдра равен одной трети длины волны, |
|
|
при этом периметр витка спирали около |
|
|
одной длины волны. Именно в этом |
|
|
случае имеет место режим осевого из- |
Рис. 2.1 |
|
лучения с круговой поляризацией. Раз- |
||
|
личают цилиндрические и конические спирали, последние характеризуются большей полосой частот. В данной работе исследуются две цилиндрические СА с экраном, оптимизированные под диапазон частот 1.7–2.7 ГГц (НЧ спиральная антенна) и 2.5–4 ГГц (ВЧ антенна). Экспериментальные частотные зависимости коэффициента отражения в тракте питания этих антенн приведены на рис. 2.2.
|
|
|
|
|
|
|
|
|
f, ГГц |
|
0 1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
5.5 |
6 |
–5 |
|
|
ВЧ-спираль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
|
–15 |
|
|
|
|
|
|
|
|
|
|
–20 |
|
|
|
|
|
|
|
|
|
|
|
НЧ-спираль |
|
|
|
|
|
|
|
|
|
–25 |
|
|
|
|
|
|
|
|
|
|
–30 |
|
|
|
|
|
|
|
|
|
|
|S11|, дБ |
|
|
|
|
Рис. 2.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 2.3 показаны качественно диаграммы направленности СА в полосе |
||||||||||
частот. Основным рабочим диапазоном СА считается интервал 0,7 < ka < 1,3, в |
||||||||||
котором она имеет осевое излучение и круговую поляризацию (k = 2π |
– |
|||||||||
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
11 |
|
|
|
|
|
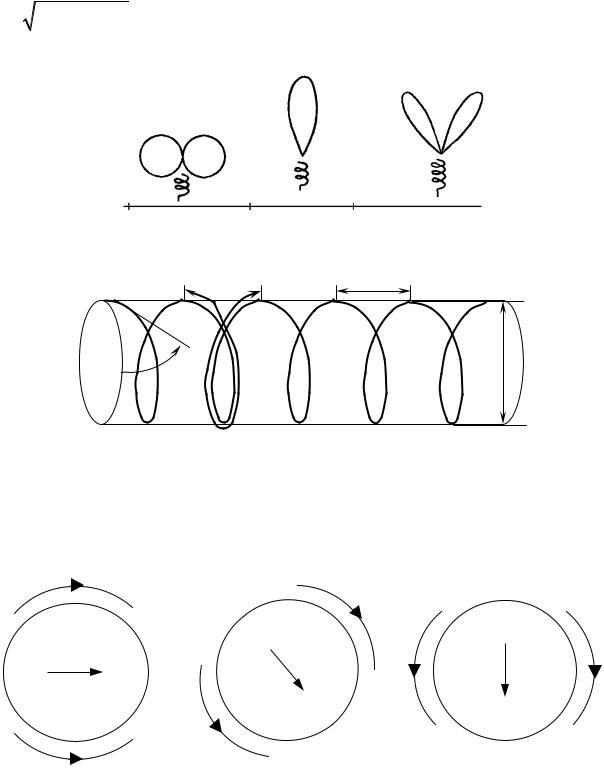
волновое число, a – радиус). При k a << 1 ДН спиральной антенны близка по форме к ДН диполя Герца, а при k a >> 1 она имеет воронкообразный характер.
Геометрия цилиндрической СА приведена |
на рис. 2.4. Здесь введены |
|||
следующие обозначения: 2a – диаметр |
СА; |
d – шаг витка спирали; |
||
|
|
|||
L = |
(2πa)2 +d 2 |
– длина витка спирали; |
α – угол подъема витка спирали, |
|
град. (обычно выбирают 12° ≤ α ≤15°); N – число витков.
0 |
0,7 |
1,3 |
ka |
Рис. 2.3
d
α
2a
L
Рис. 2.4
Рис. 2.5 поясняет механизм формирования поля круговой поляризации в режиме осевого излучения СА. При длине витка СА, близкому к длине волны, в антенне устанавливается режим бегущей волны тока и в каждый момент времени одному витку СА можно поставить в соответствие два одина-
|
|
|
E |
|
|
E |
|
|
|
|
E |
а |
б |
в |
Рис. 2.5
12
ковых синфазных изогнутых диполя. В частности, на рис. 2.5, а, б, в последовательно, в трех разных моментах времени виток эквивалентен двум изогнутым диполям, принимающим различные угловые положения в плоскости витка. Результирующий вектор напряженности излученного электрического поля вращается с постоянной длиной.
ДН спиральной антенны как ДН антенной решетки, состоящей из кольцевых плоских излучателей. Для приближенного расчета диаграммы направленности СА ее удобно рассматривать как систему, состоящую из N одинаковых элементов, расположенных вдоль продольной оси z с шагом d. Такая система носит название одномерной (линейной) антенной решетки. Ее элементами в данном случае являются неплоские витки спирали. Они возбуждены со сдвигом фаз от витка к витку ψ = kd . В соответствии с теоремой перемножения диаграмм направленности ДН такой антенной решетки представляет собой произведение множителя решетки (системного множителя) Fс (θ) и характеристики направленности ее элемента – в данном случае витка
спирали Fв (θ):
F(θ) = F |
(θ)F |
(θ). |
(2.1) |
с |
в |
|
|
Системный множитель. В общем случае, когда в решетке скачок фазы ψ между соседними элементами имеет произвольное значение, модуль системного множителя, входящего в (2.1), представляется выражением
|
|
N |
|
|
ψ |
|
||||
|
|
sin |
|
kd sin θ− |
|
|
|
|
||
|
|
2 |
|
|||||||
F (θ) = |
|
|
|
|
kd |
|
. |
|||
|
|
|
|
|
||||||
с |
|
|
kd |
ψ |
|
|||||
|
|
N sin |
2 |
sin θ− |
|
|
|
|
||
|
|
|
|
|||||||
|
|
|
|
|
kd |
|
||||
В нашем случае ψ = k d и входящее в (2.2) отношение нице, с учетом этого:
|
|
N |
|
|
|
||
|
|
|
|
||||
|
|
sin |
|
kd (1 |
−sin θ ) |
|
|
|
|
2 |
|||||
F (θ) = |
|
|
|
|
|
. |
|
|
|
|
|
||||
с |
|
N sin kd (1 |
−sin θ ) |
|
|||
|
|
|
|||||
|
|
|
2 |
|
|
||
(2.2)
ψ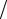 kd равно еди-
kd равно еди-
Диаграммы направленности витка спирали. Характеристика направ-
ленности такого витка известна из теории антенн, она имеет две составляющие – по ортам сферической системы координат eθ и eα [4], [5] (рис. 2.6):
13
