Вклад каждого вибратора в полное поле излучения ВК определяется амплитудой тока, наведенного на элементе. На рис. 6.3 приводится распределение амплитуды тока по излучателям для 15-элементной антенны. Видно, что наиболее сильно возбуждаются два первых директора и активный вибратор.

В результате синфазного сложения полей в осевом направлении антенна имеет довольно узкий лепесток ДН. На рис. 6.4 приводится диаграмма направленности 15-элементной ВК, на рис. 6.5 ее сечения в Е- и Н- плоскостях.

6.2. Математическое описание вибраторных антенных решеток

Для проектирования антенных решеток и оптимизации их характеристик необходимо наличие точной и высокоэффективной в вычислительном отношении математической модели, поскольку многоэлементные ВК имеют большое число степеней свободы (длины вибраторов, расстояние между ними). Математическое описание можно свести к системе связанных интегральных уравнений относительно неизвестных функцийраспределения тока в каждом элементе.

6.2.1. Система связанных интегральных уравнений для многоэлементной антенной решетки ВК

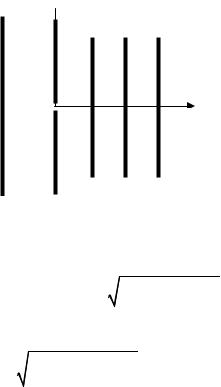
Математическая модель ВК сводится к системе связанных интегральных уравнений, порядок которой совпадает с количеством элемента. Например, для пятиэлементной антенны, представленной на рис. 6.6. искомыми являются пять функций распределения токов в рефлекторе, активном элементе и трех директорах.

Основываясь на тех же допущениях, что и при выводе уравнения Поклингтона одиночного вибратора (т. е. наличие сильного скин-эффекта, приближение тонкого провода) [1], можно сформулировать систему уравнений относительно неизвестных токов на каждом элементе ВК:

65

вибратора и точкой наблюдения на поверхности j-го вибратора, из (6.2) вид-

66

Значения стороннего электрического поля во всех строчках системы, кроме второй, равняются нулю, что объясняется наличием возбуждающего источника лишь у второго элемента.

Физический смысл системы интегральных уравнений (6.1) заключается в том, что каждая строчка – это запись граничного условия для касательной компоненты электрического поля на поверхности вибратора. Интегралы в правой части любой строки системы (6.1) – это вклад в поле на поверхности одного из вибраторов от каждого из N элементов антенной решетки, таким образом, общее число интегралов в системе равно квадрату числа элементов решетки.

Полученная система (6.1) описывает в самосогласованной постановке систему из N вибраторов с учетом взаимного влияния их друг на друга. В частном случае, при отсутствии взаимной связи (например, в случае значительного междуэлементного расстояния, т. е. при d → ∞), ядра системы (6.1) стремятся к нулю. Легко убедиться, что в этом случае система распадается на N независимых систем относительно тока в каждом уединенном вибраторе (т.е. на N независимых уравнений Поклингтона).

6.2.2. Решение системы связанных ИУ

Система (6.1) является обобщением уравнения Поклингтона для одиночного элемента и решается в пять этапов:

1-й этап. Выбираем систему базисных функций f1n (z), f2n (z), ..., fNn (z) по которым раскладывается предполагаемое решение на первом, втором и N-м вибраторах.

При этом возможна ситуация, в которой число базисных функций на каждом вибраторе неодинаково:N1 ≠ NN , а их вид на разных вибраторах разный. Получается система уравнений

67

2-й этап. Подставляем разложение (6.3) в исходную систему интегральных уравнений (6.1) и, меняя порядок суммирования и интегрирования, получаем:

(6.4)

3-й этап. Формируем систему линейных алгебраических уравнений на основе метода Галеркина. На этом этапе конкретизируем и упростим ситуацию, будем считать, что ток на каждом вибраторе описывается тремя базисными функциями. Далее, последовательно умножив правую и левую части уравнений системы (6.4) на проекционные функции fm (z) , получим систему линейных алгебраических уравнений (СЛАУ) M = 3N порядка относительно неизвестных базисных коэффициентов на каждом вибраторе:

68

−L

причем вектор-столбец левых частей для ВК имеет вид

69

где 2U01 – напряжение дельта-источника, включенного в центре активного элемента (центральный сегмент активного элемента имеет 5-й порядковый номер), остальные элементы вектора [U] равны нулю; элементы матрицы [Z] –

−L −L

вектор неизвестных базисных коэффициентов.

4-й этап. Решаем систему уравнений (6.6) любым известным способом, например методом Гаусса. В результате решения будут найдены базисные коэффициенты токов.

180

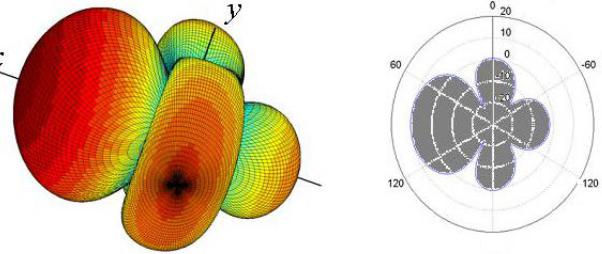
Рис. 6.7

5-й этап. По найденным коэффициентам на основе (6.3) восстанавливается ток в каждом вибраторе, затем находится входное сопротивление активного вибратора и ДН всей системы.

Результаты решения системы и вычисления ДН 5-элементной ВК (рис.6.6) представлены на рис. 6.7.

70