
- •1.1. Введение, теоретические сведения
- •1.2. Экспериментальная установка
- •1.3. Лабораторный эксперимент
- •1.4. Контрольные вопросы
- •1.5. Содержание отчета
- •2. ИССЛЕДОВАНИЕ СПИРАЛЬНОЙ АНТЕННЫ
- •2.1. Введение. Теоретические сведения
- •2.2. Экспериментальная установка
- •2.3. Проведение измерений
- •2.4. Контрольные вопросы
- •2.5. Содержание отчета
- •3. ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ РУПОРНОЙ АНТЕННЫ
- •3.1. Теоретические сведения
- •3.2. Методика измерения коэффициента усиления антенны
- •3.3. Лабораторный макет
- •3.4. Проведение измерений
- •3.5. Обработка результатов измерений
- •3.6. Контрольные вопросы
- •3.7. Содержание отчёта
- •4. ИССЛЕДОВАНИЕ ЗЕРКАЛЬНОЙ АНТЕННЫ
- •4.1. Введение. Принцип действия зеркальной антенны
- •4.2. Теоретические сведения
- •4.2. Экспериментальная установка
- •4.3. Эксперимент
- •4.4. Обработка результатов эксперимента.
- •4.5. Контрольные вопросы
- •4.6. Содержание отчета
- •5. ВЛИЯНИЕ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ НА ДИАГРАММЫ НАПРАВЛЕННОСТИ АНТЕНН
- •5.1. Идея метода зеркальных изображений
- •5.2. Применение метода зеркальных изображений к антеннам, размещенным над проводящей плоскостью
- •5.3. Обобщение на антенны с произвольно поляризованным излучением
- •5.4. Интерференция полей антенны и ее зеркального изображения
- •5.5. Частные случаи
- •5.6. Интерференционные множители
- •5.7. Экспериментальная установка
- •5.8. Проведение измерений
- •5.9. Обработка результатов и теоретические расчеты
- •5.10. Контрольные вопросы
- •5.11. Содержание отчета
- •6. ИССЛЕДОВАНИЕ МНОГОЭЛЕМЕНТНОЙ АНТЕННОЙ РЕШЕТКИ «ВОЛНОВОЙ КАНАЛ»
- •6.1. Общие сведения
- •6.2. Математическое описание вибраторных антенных решеток
- •6.2.1. Система связанных интегральных уравнений для многоэлементной антенной решетки ВК
- •6.2.2. Решение системы связанных ИУ
- •6.2.3. Метод наведенных ЭДС
- •6.3. Описание лабораторного макета
- •6.4. Задание и указания к выполнению работы
- •6.4.1. Измерение КСВ ВК1 и ВК2 в полосе частот 2…3 ГГц
- •6.4.2. Экспериментальное исследование ДН ВК1 в Е- и в Н-плоскостях на заданных дискретных частотах из интервала 2.35…2.45 ГГц
- •6.4.3. Расчет основных характеристик ВК на основе электродинамического моделирования в специализированных пакетах
- •6.5. Требования к содержанию отчета
- •6.6. Контрольные вопросы
- •7. ИССЛЕДОВАНИЕ МИКРОПОЛОСКОВОЙ АНТЕННОЙ РЕШЕТКИ
- •7.1. Общие сведения
- •7.2. Математическое описание МПА
- •7.3. Лабораторный макет
- •7.4. Программа работ
- •7.4.1. Измерение КСВ МПАР в полосе частот 3.0…4.0 ГГц
- •7.4.2. Экспериментальное исследование ДН МПАР
- •7.4.3. Расчет ДН МПАР на основе приближенной модели
- •7.4.4. Измерение отношения «вперед/назад»
- •7.4.5. Измерение ДН по кросс поляризации (выполняется по указанию преподавателя)
- •7.4.6. Расчет характеристик МПАР на основе моделирования в специализированном пакете
- •7.5. Требования к содержанию отчета
- •7.6. Контрольные вопросы
- •Список литературы
- •Оглавление
4.6. Содержание отчета
Отчет должен содержать:
•Структурную схему установки;
•Таблицы и графики экспериментальных ДН облучателей и ЗА с ними;
•Расчетные графики поля в раскрыве ЗА;
•Расчетные ДН антенн в виде графиков;
•Расчет ШГЛ, КНД, КРЛ, УБЛ;
•Выводы.
5. ВЛИЯНИЕ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ НА ДИАГРАММЫ НАПРАВЛЕННОСТИ АНТЕНН
При расположении антенны над проводящей поверхностью ее ДН претерпевает существенные изменения по сравнению с характеристиками в свободном пространстве. В некоторых частотных диапазонах (СДВ, ДВ, СВ) земля и водная поверхность могут рассматриваться как поверхности с хорошей проводимостью, в связи с этим исследование влияния подстилающей поверхности на характеристики антенн и ее учет при разработке, размещении и выборе поляризации излучения антенн позволяет улучшить характеристики радиотехнических систем.
Учет эффектов влияния проводящей поверхности на ДН антенн в лабораторной работе проводится на основе метода зеркальных изображений. Он позволяет провести решение электродинамических задач при наличии границ раздела сред и найти электрические и магнитные поля, создаваемые антенной, расположенной вблизи проводящей поверхности. Суть метода заключается в том, что, путем введения фиктивного источника, задача поиска полей в присутствии проводящей поверхности сводится к более простой задаче в свободном пространстве. При этом величину поля, создаваемого фиктивным источником, и его расположение определяют из условия обеспечения граничных условий.
В данной лабораторной работе экспериментально и теоретически исследуются характеристики антенны в виде открытого конца волновода, расположенного над проводящей поверхностью, и определяется поведение ДН антенны при изменении высоты подъема антенны для различных поляризаций излучаемого поля.
50

5.1. Идея метода зеркальных изображений
Рассмотрим следующую ситуацию. Имеется источник поля, расположенный над бесконечной идеально проводящей поверхностью S (рис. 5.1), которая делит пространство на два полупространства – 1 и 2. В полупр о- странстве 2 поле отсутствует, так как оно экранировано от источника. Требу-
ется найти поле в полупространстве 1, кото- |
|
|
Источник |
|||||
рое, очевидно, не совпадает с полем источни- |
|
|
|
|
||||
ка в отсутствие экрана. С формально-матема- |
|
1 |
Eτ = 0 (Hn = 0) |
|||||
тической точки зрения влияние экрана сказы- |
S |
|
|
|
||||
2 |
|
|
||||||
вается в том, что на его поверхности должно |
|
Рис. 5.1 |
||||||
выполняться граничное условие |
|
|
||||||
Eτ |
|
s = 0, Hn |
|
s = 0. |
|
|
(5.1) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||
Метод зеркальных изображений позволяет рассчитать поле в полупространстве 1 путем замены экрана зеркальным изображением источника в нем. Искомое поле представляется тогда суммой полей истинного источника и его зеркального изображения. На месте удаленного экрана должно при этом обеспечиваться выполнение условия (5.1). Рассмотрим применение метода на примере вертикального и горизонтального диполя Герца с моментом pэ=il (i -
ток, l-длина диполя) (рис. 5.2). На основе метода зеркальных изображений откажемся от проводящей границы раздела и запишем выражение для напряженности электрического поля, создаваемого в дальней зоне диполя Герца с момен-
том pэ в следующем виде: E1 = eθ pэ ( j k) e− jkr sin (θ). На фиктивной границе
4π r
двух сред орт eθ можно представить как сумму нормальной и касательной к
поверхности, составляющей со |
своими амплитудными коэффициентами |
|||||||
E |
= (e |
n |
sin(θ) −e |
τ |
cos(θ)) |
pэ |
( j k) e− jkr sin (θ). Из приведенного выражения |
|
|
||||||||
1 |
|
|
|
4π |
|
r |
||
|
|
|
|
|
|
|
||
видно, что одиночной диполь имеет отличную от нуля касательную к поверхности составляющую электрического поля, что не удовлетворяет ГУ (5.1). В связи с этим необходимо осуществить выбор расположения и фазы дипольного момента изображения, при которых обеспечивается выполнение ГУ. Поле мнимого изображения должно скомпенсировать касательную составляющую электрического поля оригинала, следовательно, моменты оригинала и изображения должны быть синфазными. В этом случае поле, создаваемое изображением, за-
51

пишется как E2 |
= (en sin(θ) +eτ cos(θ)) |
pэ |
( j k) e− jkr |
sin (θ). В результате |
|
4π |
|||||
|
|
r |
|
суммарное поле будет удовлетворять ГУ (5.1) и таким образом, поле в дальней зоне системы из двух источников окажется эквивалентным полю диполя над проводящей поверхностью.
|
|
|
z |
|
|
|
|
|
|
Pэ |
|
|
Pэ |
|
|
θ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Eτ = 0 |
|
|
|
|
|
|
|
|
|
~ |
Eτ = 0 |
|
eτ |
|
|
|
|||
|
|
|
o |
|
|
|
|
|
|
|
|
|
Pэ |
|
E |
en |
E2 |
||
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.2
Повторяя изложенные рассуждения для горизонтально расположенного диполя можно сделать вывод, что в этом случае моменты должны быть противофазными.
5.2. Применение метода зеркальных изображений к антеннам, размещенным над проводящей плоскостью
Как известно, любую антенну можно представить совокупностью элементарных электрических и магнитных диполей Герца. Поэтому очевидна законность переноса метода зеркальных изображений и на этот случай. Суть метода полностью сохраняется: чтобы найти поле антенны в полупространстве 1, нужно отбросить экран, а его действие заменить действием зеркального изображения антенны. Необходимо лишь выяснить связь между характеристиками направленности реальной антенны и ее зеркального отображения. Для удобства анализа рассмотрим отдельно случай антенны с вертикально- и горизонтально-поляризованным полями излучения.
Вертикальная поляризация. Пусть центр О1 антенны 1 поднят над поверхностью на высоту h (рис. 5.3). Центр изображения (антенны 2) должен, очевидно, находиться в зеркально-симметричной точке О2. Суммарное напряженность электрического поля обеих антенн должно иметь нулевую касательную составляющую в любой точке А на поверхности S. Определим
52
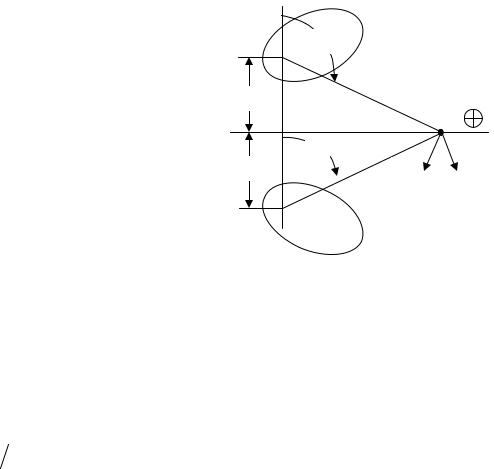
сначала в этой точке поле антенны 1. Как |
|
|
|
Fв1(θ1) |
|||||||||||
известно, в |
поле излучения |
вектор |
элек- |
|
О |
θ1 |
Fг1(θ1) |
||||||||
трического |
поля |
|
перпендикулярен |
|
|
1 |
|
|
|
||||||
E |
|
|
|
r |
|
|
|||||||||
направлению распространения, т. е. в дан- |
h |
|
|
еα |
|||||||||||
ном случае − лучу О1А; в то же время этот |
|
0 |
S |
|
|
A |
|||||||||
вектор, по нашему предположению, поля- |
h |
θ2 |
|
еθ1 |
|||||||||||
ризован в вертикальной плоскости. Следо- |
|
r |
|||||||||||||
вательно, он должен быть ориентирован по |
|
О |
2 |
Fв2(θ2) |
|||||||||||
орту eθ1. Поле излучения пропорциональ- |
|
||||||||||||||
|
|
F |
|
(θ ) |
|||||||||||
|
|
|
г2 |
||||||||||||
но |
характеристике |
направленности |
по |
|
|
|
|
2 |
|||||||
|
|
|
Рис. 5.3 |
|
|
||||||||||
направлению луча О1А. Характеристика |
|
|
|
|
|
||||||||||
направленности антенны 1 записывается как функция угла θ, отсчитываемо- |
|||||||||||||||
го от вертикали. Следовательно, ее значение по направлению луча О1А есть |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
[В/м] должно содержать множи- |
|||||
Fв1(θ1). Наконец, выражение для поля Eв1 |
|||||||||||||||
тель, учитывающий запаздывание волны по фазе и убывание ее по амплитуде |
|||||||||||||||
обратно пропорционально расстоянию от антенны. Этот множитель − функ- |
|||||||||||||||
ция Грина e− jkr r . Учитывая изложенное, получим |
|
|
|
|
|||||||||||
|
|
|
|
E |
в1 |
(A) = e |
θ1 |
e− jkr |
F |
(θ ). |
|
|
|
(5.2) |
|
|
|
|
|
|
|
|
r |
в1 |
1 |
|
|
|
|
||
|
Аналогичным образом записывается поле зеркального изображения в |
||||||||||||||
точке А: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e− jkr |
Fв2 (θ2), |
|
|
(θ) |
Eв2(A) = eθ2 r |
(5.3) |
|
где F |
– характеристика направленности антенны 2. Угол |
θ по-преж- |
||
в2 |
|
|
|
|
нему отсчитывается от вертикали, так что в данном случае он равен θ2 (см.
рис. 5.3).
Чтобы поле Eв (A) = Eв1(A) +Eв2(A), полученное суммированием (5.2) и (5.3), имело нулевую касательную составляющую относительно S, значения Fв1(θ1) и Fв2 (θ2) должны совпадать. Только в этом случае касательные составляющие обоих полей взаимно компенсируются. Заметим, что углы θ1 и θ2 в данном рассмотрении жесткосвязаны: θ1 +θ2 = π. Поэтому Fв2 (θ2)= Fв1(θ1), θ1 +θ2 = π. Это равенство означает, что характеристика направленности ан-
53

θтенны 2 должна быть зеркальным отражением харак-
|
Fв1(θ) |
теристики направленности антенны 1 (см. рис. 5.3), |
||||||||
|
а антенны должны быть возбуждены синфазно. |
|
|
|||||||
|
|
|
Особо выделим случай, когда ДН антенны 1 |
|||||||
|
|
|
||||||||
|
|
|
симметрична |
относительно направления |
θ = 90° |
|||||
|
|
|
(рис. 5.4). В таком случае ее зеркальное изображе- |
|||||||
|
|
|
ние будет совпадать с оригиналом. Следовательно, |
|||||||
|
|
|
|
F |
(θ) = F |
(θ). |
|
|
(5.4) |
|
|
θ |
|
|
в1 |
в2 |
|
|
|
|
|
|
|
Горизонтальная поляризация. В данном случае |
||||||||
|
|
|
||||||||
|
F |
(θ) |
выражение для поля антенны 1 в точке А |
E |
г1 |
(A) |
||||
|
в2 |
|
|
|
|
|
|
|
||
|
|
|
будет отличаться от выражения (5.3).Во-первых, век- |
|||||||
|
|
|
||||||||
|
|
|
тор Eг1(A), который должен быть перпендикулярен |
|||||||
|
Рис. 5.4 |
|
О1А (см. рис.5.3) |
и одновременно горизонтально |
||||||
|
|
|||||||||
|
|
поляризован, |
будет направлен по орту eα |
, перпен- |
||||||
|
|
|
||||||||
дикулярному плоскости рисунка. Во-вторых, характеристика направленности имеет индекс «г», а не «в». Таким образом,
E |
(A) = e |
α |
e− jkr |
F |
(θ |
). |
(5.5) |
г1 |
|
r |
г2 |
1 |
|
|
Поле антенны 2 также поляризовано по орту eα:
E |
(A) = e |
α |
e− jkr |
F |
(θ |
). |
(5.6) |
г2 |
|
r |
г2 |
2 |
|
|
Сумма векторов (5.5) и (5.6) должна обратиться в нуль, поскольку орт eα касателен к S. Следовательно, значения Fг1(θ1) и Fг2 (θ2) должны быть равны и противоположны по знаку:
Fг1(θ1) = −Fг2 (θ2), θ1 +θ2 = π. |
(5.7) |
Таким образом, характеристики направленности антенн являются зеркальными изображениями друг друга, но, согласно (5.7) в отличие от верт и- кальной поляризации (см. (5.4)), антенны должны быть возбуждены в противофазе.
В особом случае, когда характеристики направленности симметричны
относительно θ = 90°, получим следующее соотношение между ними: |
|
||
F |
(θ) = −F |
(θ). |
(5.8) |
г1 |
г2 |
|
|
54
