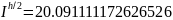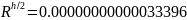Лабы 2 сем / лаба 5
.docxМОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
Отчёт к лабораторной работе №5
Численное интегрирование
Задачи №5.1, 5.2
Группа: ТФ-09-19
Студент: Быковская В.
Вариант №3
Москва 2021
Задача
5.1. Вычислить значение интеграла
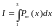 ,
где
,
где
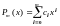 ,
с помощью элементарных квадратурных
формул левых прямоугольников и по
формуле индивидуального варианта.
Затем, используя априорную оценку
погрешности, оценить шаг интегрирования
h, требуемый для достижения
точности
,
с помощью элементарных квадратурных
формул левых прямоугольников и по
формуле индивидуального варианта.
Затем, используя априорную оценку
погрешности, оценить шаг интегрирования
h, требуемый для достижения
точности
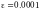 .
Вычислить интеграл с найденным шагом
интегрирования.
.
Вычислить интеграл с найденным шагом
интегрирования.
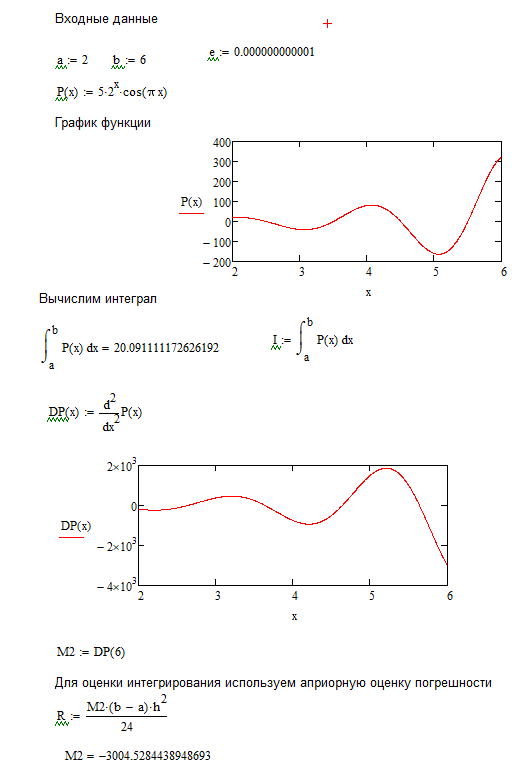
Входные данные:
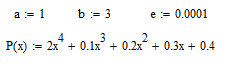
График функции P(x)
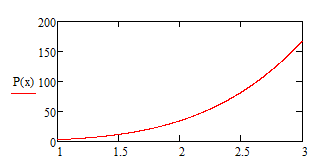
Вычислим интеграл
![]()
Для оценки шага интегрирования используем теоретическую оценку погрешности:
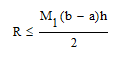
Найдем константу М1
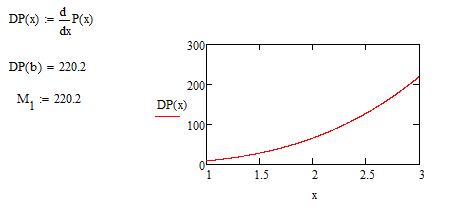
По графику видно, что максимум производной достигается в точке B
Для нахождения шага воспользуемся априорной оценкой погрешности
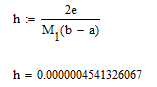
Количество отрезков разбиения:
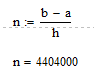
Вычислим значение интеграла по составной формуле левых прямоугольников
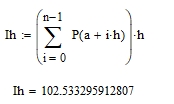
Полученная величина погрешности
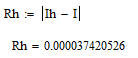
Вычислим значение интеграла по формуле Симпсона:
Значение
4 производной:
![]()
Шаг интегрирования:
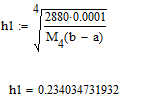
Количество отрезков:
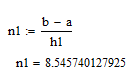
Возьмем целое количество отрезков и скорректируем шаг интегрирования:
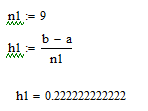
Вычислим значение интегралла:
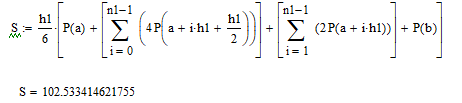
Величина погрешности:

Меньше заданной точности , занчит вычисления произведенены правильно
Найденное точное значение интеграла
|
Число разбиений отрезка n Шаг интегрирования h |
Значение
интеграла, вычисленное по составной
формуле
Величина
погрешности интеграла, вычисленного
по составной формуле
|
Метод Левых прямоугольников |
|
|
Метод индивидуального варианта Метод Симпсона |
|
|
Задача
5.2. Вычислить интеграл
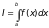 с точностью
с точностью
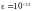
Найдем значение через формулу трапеций
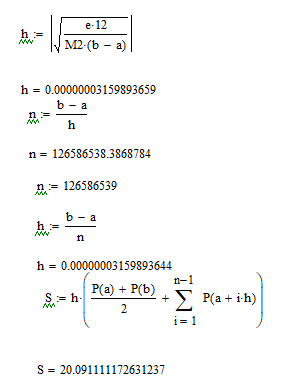
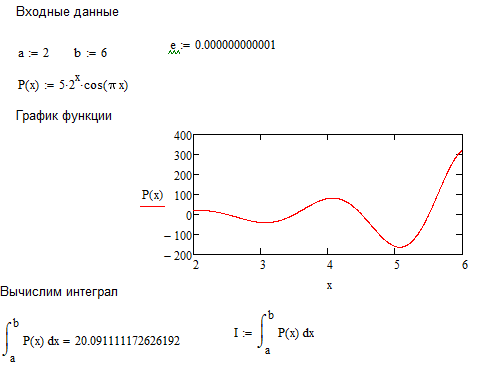
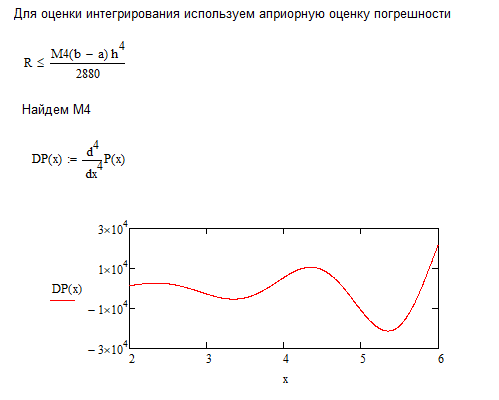





I= 20.091111172626192 |
Метод левых прямоугольников |
Метод Симпсона |
Число разбиений отрезка
Значение интеграла
Величина погрешности
Уточненное значение интеграла
Величина погрешности |
= 20.091111172631237
|
9420 = 20.091111172626313 = 0.00000000000012079
|

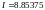

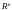
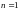
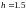
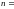 126586539
126586539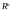 =
0.00000000000504485
=
0.00000000000504485