дз1фкп_другой вариант1

Задание №1

Изменить порядок интегрирования:

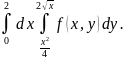
Решение:

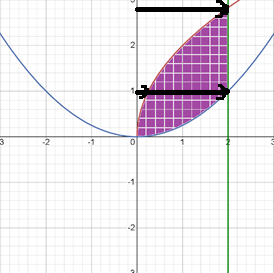Построим графики функций, указанные в пределах внутреннего интеграла. Тогда они будут пересекаться в точках со следующими координатами:

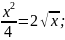
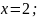- по условию

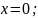
Выразим y подставив 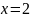и :

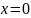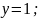
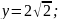
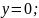
Т.о. графики пересекаются в точках 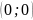, 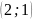и .

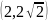Т.к. нам нужно сделать внешнем интеграл по dy, то проведем прямую параллельную оси абсцисс, пересекающую оба графика. Сначала она пересечёт график функции 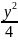, потом 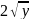. Сама область D разбивается на две част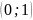и: и 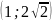. Изменим порядок интегрирования:

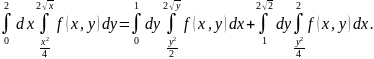
Ответ: .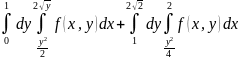

Задание №2

Вычислить объём тела ограниченного поверхностями:

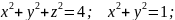
Решение:

Построим графики плоскостей. На нём видно, что снизу тело ограничено снизу 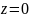, а сверху .

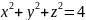Спроецируем эти поверхности на плоскость XOY.

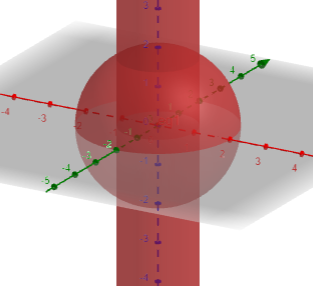Формула нахождения объёма:

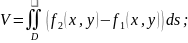
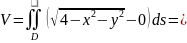
Запишем эту формулу сразу в полярной системе координат с помощью формул:

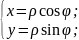
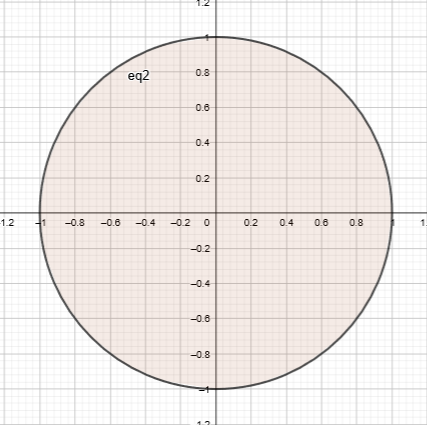И т.к. область D разбита на две части получим:

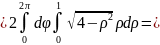
Подведем 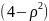под дифференциал, получим 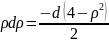и найдём внутренний интеграл. Также сразу вычислим внешний интеграл, потому что пределы внутреннего не содержат функций с аргументом :

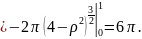
Ответ:

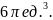
Задание №3

Вычислить площадь числа поверхности (а), вырезанной поверхностями

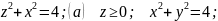
Решение:

Начертим графики заданных функций. Поверхность (а) – цилиндр, параллельный плоскости YOZ, а остальные поверхности: цилиндр параллельный плоскости XOY и плоскость XOY. Спроецировав 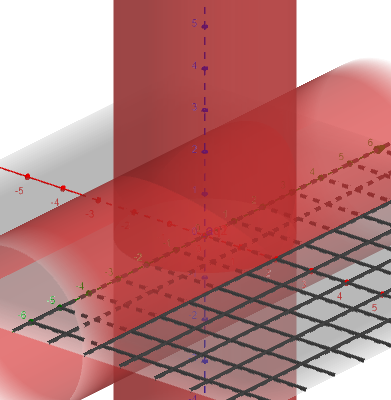получившиеся кривые на плоскость XOY получим две окружность с радиусом R=2. Область D находится в этой окружности.

Формула нахождения площади:

;

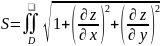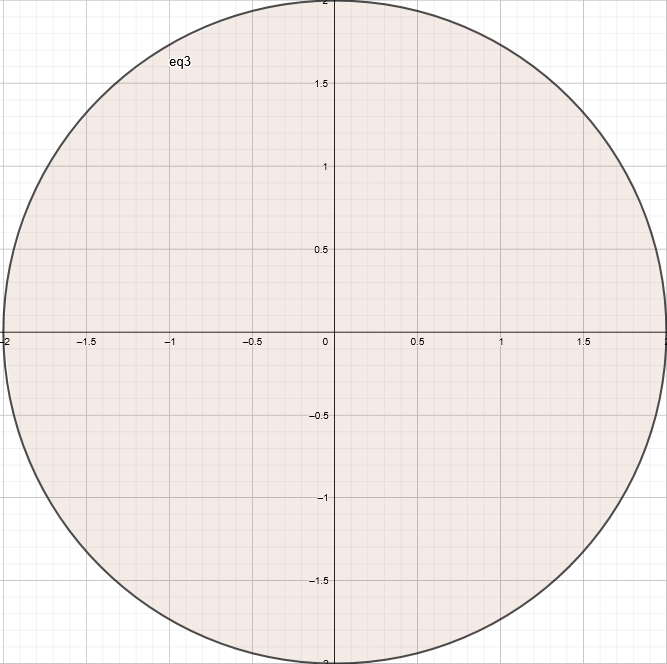Найдём 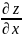и 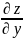и подставим в формулу, а так же перейдём к полярной системе:

; ;

.

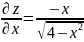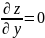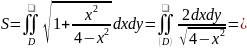
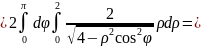
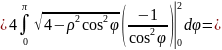
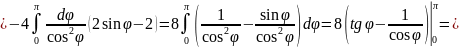
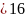Ответ: .

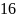Задание №4

1. Проверить зависит ли криволинейный интеграл от пути интегрирования.

2. Вычислить криволинейный интеграл.

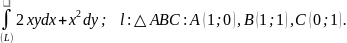
Решение:

1. Вычислим 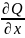и :

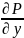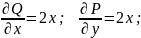
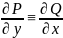– тождество верно, а значит криволинейный интеграл не зависит от пути интегрирования

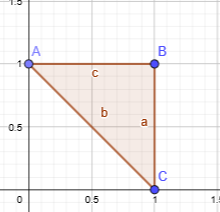
2. Начертим график заданных кривых. Видно x меняется на отрезке 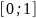, и y на отрезке .

Т.к. интеграл не зависит от пути интегрирования, то он будет равен нулю, но чтобы доказать это мы его вычислим криволинейный интеграл по формуле:

.

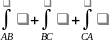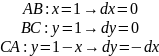
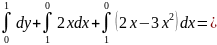
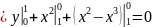
Ответ: не зависит от пути интегрирования; 0.