
Билеты
.pdf
1) Электрические заряды и их взаимодействие, закон Кулона. Электрический заряд определяет свойство тел взаимодействовать с другими заряженными телами через электростатические поля, создаваемые этими зарядами.
Взаимодействие тел может быть положительным (если тела/заряды притягиваются) и отрицательным (если тела/заряды отталкиваются). Очевидно существование элементарного заряда. Им обладают большинство частиц (протон, позитрон, электрон).
Заряд равен целому числу таких элементарных зарядов.
q Ne,
1e 1,6 *1019 Кл.
Если заряд неподвижен, то он в простанстве создает электростатическое поле. Если заряд двигается без ускорения – еще и магнитное поле. Если двигается с ускорением – электромагнитное поле, которое распространяется в виде электромагнитных волн.
Точечный заряд – заряженное тело, линейными размерами которого можно пренебречь.
Сила взаимодействия двух зарядов определяется по закону Кулона:
F k |
q1q2 |
; F k |
q1q2 |
r . |
|
r 2 |
r 2 |
||||
|
|
0 |
k 9 *10 9 Н * м2 .
Кл2
1. Заряд распределяется равномерно по всей длине.
|
dq . |
Вводится понятие о линейной плотности заряда. |
dl |
2.Заряд распределяется равномерно по поверхности заряженного тела. Вводится понятие о поверхностной плотности заряда.
dSdq .
3.Заряд распределяется равномерно по всему объему.
|
|
dq |
. |
Вводится понятие об объемной плотности заряда. |
|
||
|
dV |
||
2) Напряженность – силовая характеристика, равная отношению силы, действующей со стороны этого поля, на точечный заряд, помещенный в данную точку.
Направление E |
совпадает с направлением F. |
||||
E |
F |
|
kQ |
r . |
|
|
|
||||
|
q |
|
r 2 |
0 |
|
kQ
Er 2 .
диэлектрическая проницаемость среды.
Электрическое поле — одна из составляющих электромагнитного поля, особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела.
Напряженность поля точечного заряда. Обозначим: q - заряд, создающий поле,
q0 - заряд, помещенный в поле (внешний заряд).
Закон Кулона: . Напряженность поля:  .
.
Тогда напряженность поля точечного заряда: 
Принцип суперпозиции.
Если в точке пространства существуют поля, создаваемые несколькими зарядами, то напряженность в данной точке поля равна векторной сумме напряженностей полей.
E E1 E2 E3
... Е
... Е.

3) Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур.
Теорема Гаусса — |
основная |
теорема электродинамики, |
которая |
применяется для |
вычисления |
электрических полей, |
входит в |
систему уравнений Максвелла. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченной этой поверхностью Теорема Гаусса. Поток вектора напряженности через замкнутую
поверхность равен алгебраической сумме зарядов, охватываемой этой суммой зарядов, деленной на проницаемость среды и электрич.
1 k
постоянную. 0 1 qi.
В работе Остроградского формула записана в следующем виде:
где ω и s — дифференциалы объёма и поверхности соответственно. В современной записи ω = dΩ — элемент объёма, s = dS — элемент
поверхности. 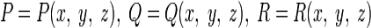
— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
4)Теорема применяется для расчета электростатических полей.
E 2S |
S E |
|
. |
|
|||
|
0 |
2 0 |
|
1. Поле бесконечно длинного заряженного цилиндра.
|
Е 2 al |
l . |
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|||
заряд распределен по всей длине |
E |
|
|
|
|
|
|
|
|
|
|
|
2 0 a |
|
|
|
|
|
|
|
|||
|
|
Е 2 al 2 R . |
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
заряд распределен по всей поверхности EA |
|
R |
, |
EB |
|
|
, EC 0 |
||||
0 a |
|
0 |
|||||||||
|
|
|
|
|
|
|
|
||||
2. Поле заряженной сферы.
заряд распределен по всей поверхности
Е4 r2 4 r2 .
0
E |
|
|
R |
, |
E |
|
|
|
|
, |
E 0 |
|
0 r2 |
|
|
|
|||||||
|
A |
|
|
|
B |
|
0 |
|
C |
|
|
|
|
|
|
|
|
4 |
R3 |
||
|
Е 4 r |
2 |
|
3 |
|||||||
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
||||
заряд распределен по всему объему |
EA |
|
R3 |
, EB |
R |
||||||
|
3 0 r2 |
3 0 |
|||||||||
3.Поле заряженной плоскости
Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием S, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2E S. Применив теорему Гаусса, получим:
 из которого
из которого

5) Потенциальность постоянного электрического поля. |
|
|
|
||||||||||||||||||||||||
Работа силы F на элементарном перемещении dl равна |
|
|
|
|
|||||||||||||||||||||||
dA Fdl Fdl cos |
|
|
1 |
|
|
|
QQ0 |
dl cos |
dl cos dr |
||||||||||||||||||
|
4 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dA |
1 |
|
|
QQ0 |
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0 |
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Работа при перемещении Q0 из точки 1 в точку 2. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
r2 |
|
|
|
|
|
r 2 |
|
dr |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
||||||||||
A1 2 dA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 0 |
|
r |
2 |
|
4 0 |
r1 |
|
|
r2 |
|
|
|||||||||||||||
|
r |
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
не зависит от |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
траектории перемещения. Следовательно эл.стат. поле точечного заряда является потенциальным, а эл.стат. силы консервативными.
Потенциал в какой либо точке эл.стат. поля есть физическая величина, определяемая потенциальной энергией положительного заряда, помещённого
|
|
1 |
|
Q |
|
|
|
|
|
в эту точку. |
4 0 |
|
r |
Разность потенциалов двух точек равна работе при перемещении единичного положительного заряда из точки 1 в точку 2.
2
1 2 El dl
1
Напряжённость электрического поля точечного заряда
Согласно формуле Гаусса — Остроградского, а также используя уравнениеМаксвелла  , легко получить:
, легко получить:
где qin — заряд, находящийся внутри замкнутой поверхности S, объемом V. В качестве поверхности интегрирования возьмем сферу (центральная симметрия), тогда
В силу центральной симметрии поля точечного заряда:
6) Потенциал, связь между напряженностью и потенциалом.
Потенциал – энергетическая характеристика поля, численно равная работе, которую нужно совершить, чтобы переместить точечный заряд из данной точки в бесконечность.
Ввиду того, что работа – скалярная величина, и потенциал – скаляр.
Понятие о потенциале можно ввести для электростатического поля ввиду того, что работа по перемещению заряда не зависит от формы траектории, по которой осуществляется перенос, а только от положения точки.
Примечание автора. Путем графической иллюстрации и вывода формул была получена следующая формула.
qEdl 0 Edl 0.
Циркуляция вектора Е вдоль замкнутого контура равна нулю.
Циркуляция – необходимое и достаточное условие для введения скалярного потенциала. Доказательством является независимость работы от вида движения и формы траектории.
|
A |
|
|
||
|
Edl cos(E,dl). |
|
|||
q |
|
Следует, что математически потенциал – интеграл |
|||
|
r |
||||
|
|
|
|
||
от напряженности электрического поля. Отсюда, напряженность – производная от потенциала.
Тогда, учитывая, что E ориентирован в пространстве, Ex ddx .
«Минус» означает, что действующая сила (напряженность) направлена в сторону убывания потенциала, то есть туда, где потенциальная энергия заряда будет иметь наименьшую величину.
Egrad
kqr .
Эквипотенциальная поверхность — понятие, применимое к любому потенциальному векторному полю, например, к
статическому электрическому полю или к ньютонову гравитационному полю. Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение.
Втрёхмерной декартовой системе координат уравнение принимает форму:
Вдекартовой системе координат оператор Лапласа записывается в форме  и уравнение Пуассона принимает вид:
и уравнение Пуассона принимает вид:
.

7)Объемная плотность заряда
|
|
|
|
|
|
|
qi |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(r |
ri |
) |
|
|
|
|
|||||||||
|
|
|
|
|
Напомним, что |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
f (r ) (r |
ri |
)dv f (ri |
) 0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда энергия W |
1 |
i dVi |
|
1 |
i dSi |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
i |
Vi |
|
|
|
|
2 |
i |
Si |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как Si |
0 |
то |
W |
1 |
i dVi |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
|
i Vi |
|
|
|
|
|
|
|
|
|
|
|
|||
Где i - потенциал в точке i-го заряда, а V - объем i -го заряда. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
(cob) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
(cob) |
|
|
|
|
|
|
|
|||||||||
W |
|
i |
i |
dVi |
|
|
i |
dVi |
|
|
qi i (r |
ri |
)dVi |
||||||||||
2 |
2 |
2 |
|||||||||||||||||||||
|
i |
|
|
|
i V |
|
|
|
|
|
i |
V |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||
Итак:
W1 qi i Wcob
2 i
Таким образом, энергия взаимодействия точечных зарядов:
W1 qi i
2 i
При этом для одного заряда q в точке с потенциалом φ энергия
Wq
-энергия заряда q в поле .
8) Диполь.
Электрический диполь —совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга Потенциальная энергия электрического диполя в электрическом поле
равна 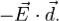 Любая в целом электронейтральная система, содержащая
Любая в целом электронейтральная система, содержащая
электрические заряды, в некотором приближении может рассматриваться как электрический диполь с
моментом  где
где  — заряд i-го элемента,
— заряд i-го элемента,  — его радиусвектор.
— его радиусвектор.
Дипольный момент — физическая величина, характеризующая электрические свойства системы заряженных частиц. Для системы из N
частиц дипольный момент равен
 ,
,
где qi — заряд частицы с номером i, а  — её радиус-
— её радиус-
вектор;  — число положительно/отрицательно заряженных частиц, N = N + + N − ,
— число положительно/отрицательно заряженных частиц, N = N + + N − , 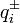 — их заряды.
— их заряды.
Дипольный момент нейтральной системы зарядов не зависит от начала координат, а определяется относительным расположением
(и величинами) зарядов в системе.
Поле диполя вычисляется по формуле:
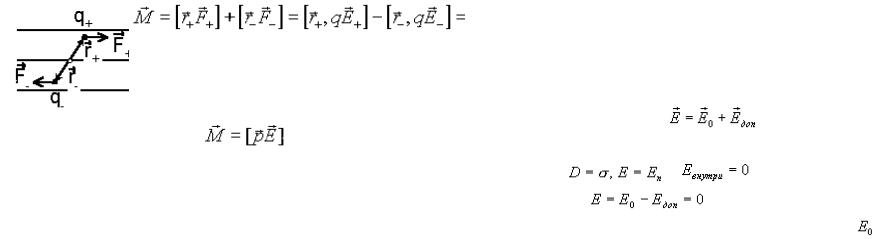
8a) Диполь во внешнем электрическом поле
Найдем момент сил, действующих на диполь в однородном электрическом поле. Пусть положения положительного и отрицательного зарядов относительно центра диполя характеризуются векторами r+ и r- , соответственно. Тогда, в соответствии с определением момента сил, имеем
Так как по определению  , то окончательно получим
, то окончательно получим
(3.9)
Рис. 3.4
Момент сил, очевидно, равен нулю, когда векторы p и E коллинеарны, однако устойчивым положением является только такое положение, когда они еще и совпадают по направлению. В однородном поле, очевидно, F+ + F_= 0.
\
9) В проводниках могут перемещаться свободно не только заряды принесенные из вне, но и микроскопические заряды, из которых состоят атомы и молекулы проводника (электроны, ионы). Поэтому при помещении незаряженного проводника во внешнее электрическое
поле 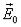 свободные микроскопические заряды будут перемещаться к его
свободные микроскопические заряды будут перемещаться к его
поверхности: положительные по полю, а отрицательные против поля
(рис.15.4). На одном конце проводника будет скапливаться избыток положительного заряда, а на другом избыток отрицательного до тех пор,
пока создаваемое этими зарядами дополнительное поле  не
не
скомпенсирует внешнее поле во всех точках внутри проводника. При
этом суммарное поле |
|
внутри проводника и на его |
|
поверхности |
|
будет |
удовлетворять |
условию |
и |
т.е. |
внутри |
проводника |
|
, а в близи проводника будет заметно |
|
отличаться от своего |
первоначального значения |
. Заряды на |
|
противоположных краях проводника называются индуктированными или наведенными.
Индуктивные заряды распределяются по внешней поверхности проводника. Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также равно нулю. На этом основана электростатическая защита.
Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля.
Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле,
заряды перераспределяются так (явление электрической индукции), что

создаваемое ими внутри проводника поле полностью компенсирует внешнее.
10)Потенциал уединенного проводника пропорционален находящемуся на нем заряду. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в тоже число раз напряженности поля в каждой точке окружающего проводника пространства, т.е.
Вводя |
соответствующий |
коэффициент |
пропорциональности, |
запишем |
или |
|
|
где С - называется электроемкостью.
Таким образом, электроемкость уединенного проводника есть физическая величина численно равная величине заряда, который необходимо сообщить данному проводнику для увеличения его потенциала на единицу. В СИ единицей емкости является Фарад (Ф).
Определим электроемкость уединенного шара. Потенциал заряженного шара радиуса R
Сравнивая с  получаем
получаем 
11) Электроемкость. Конденсаторы. Энергия электростатического
поля.
Электроемкостью (емкостью) C уединенного изолированного проводника называется физическая величина, равная отношению изменения заряда проводника q к изменению его потенциала f:
C = Dq/Df.
Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (e). Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) - это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон.
1 Ф = 1 Кл/1 В.
Конденсатором называют систему двух разноименно заряженных проводников, разделенных диэлектриком (например, воздухом). Свойство конденсаторов накапливать и сохранять электрические заряды и связанное с ними электрическое поле характеризуется величиной, называемой электроемкостью конденсатора. Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U:
C = Q/U.
В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.
Тип |
Схематическое |
Формула для |
|
|
расчета |
Примечания |
|||
конденсатора |
изображение |
|||
емкости |
|
|||
|
|
|
||
|
|
|
S - площадь |
|
Плоский |
|
|
пластины; |
|
|
C = ee0S/d |
d - расстояние |
||
конденсатор |
|
|||
|
|
между |
||
|
|
|
||
|
|
|
пластинами. |
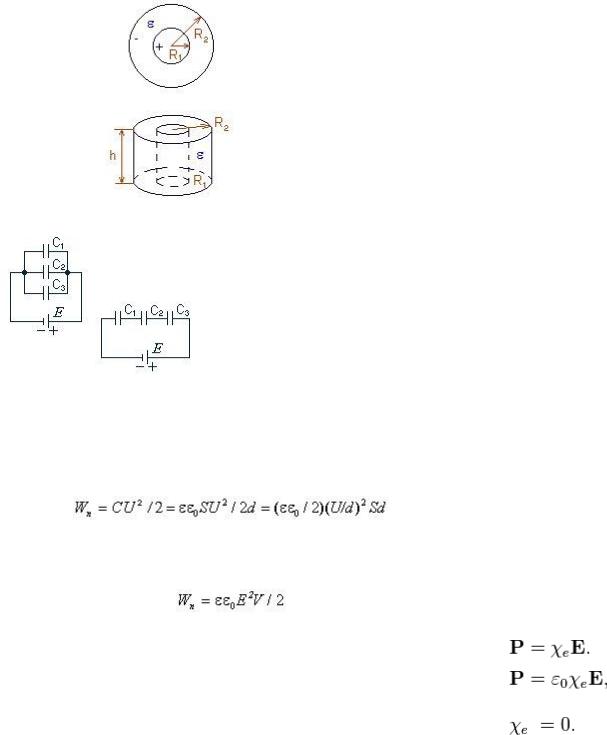
|
C = |
|
R2 и R1 - радиусы |
|
Сферический |
|
внешней и |
||
4pee0R1R2/(R2 |
- |
|||
конденсатор |
внутренней |
|||
R1) |
|
|||
|
|
обкладок. |
||
|
|
|
11a)
Цилиндрический C = 2pee0h/ln(R2/R1) h - высота цилиндров.
конденсатор
Соединение конденсаторов в батареи.
На практике конденсаторы часто соединяют в батареи - последовательно или параллельно.
При параллельном соединении напряжение на всех обкладках одинаковое U1 = U2 = U3 = U = e, а емкость батареи равняется сумме емкостей отдельных конденсаторов C = C1 + C2 + C3.
|
При последовательном соединении заряд на обкладках |
|
всех конденсаторов одинаков Q1 = Q2 = Q3, а |
|
напряжение батареи равняется сумме напряжений |
|
отдельных конденсаторов U = U1 + U2 + U3. |
Емкость всей |
системы последовательно соединенных конденсаторов |
рассчитывается из |
соотношения: |
1/C = U/Q = 1/C1 + |
1/C2 + 1/C3. |
Емкость батареи последовательно соединенных конденсаторов всегда меньше, чем емкость каждого из этих конденсаторов в отдельности.
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
11b)Вывод С для сферы:
Поместим на внешнюю сферу (радиуса R2) заряд q, а на внутреннюю (радиуса R1) --- -q. Вычислим U
--- разность потенциалов между сферами (тогда искомая емкость по определению будет равна q/U). Как известно, потенциал, создаваемый сферой вне этой самой сферы такой же, как и у точечного
заряда, |
а внутри |
потенциал равен константе, такой же, как и на поверхности. |
||||
Нас |
будет |
интересовать |
только |
область |
между |
сферами. |
В интересующей нас области потенциал от внешней сферы постоянен, а от внутренней потенциал на
расстоянии |
R |
равен |
-k |
q/R. |
(здесь k --- |
постоянная |
в законе кулона. |
k = 1/(4 pi Epsilon |
Epsilon0)) |
Мы хотим сосчитать разность потенциалов на сферах U = ((-kq/R) при R=R2) - ((-kq/R) при R=R1) = kq/R1-kq/R2=kq(R2-R1)/R1 R2, откуда находим, что емкость конденсатора = q/U =(1/k)*R1 R2/(R2-R1). Если подставить k, то получится ваша формула
12) К диэлектрикам относят вещества, в которых нет свободных зарядов или их число настолько мало, что они не оказывают существенного влияния на их характеристики. Поведение диэлектрика в электрическом поле определяется поведением его молекул, которые делятся на полярные и неполярные молекулы.
У полярных молекул (молекулы воды Н2О, соляной кислоты, аммиака и т.д.) в отсутствие электрического поля центры тяжести положительных и отрицательных зарядов не совпадают (рис.2.19), такие молекулы представляют собой диполи, которые характеризуются дипольным моментом p .
Для неполярных молекул (молекулы кислорода О2, водорода Н2, гелия Не и т.д.) в отсутствие электрического поля центры тяжести положительных и отрицательных зарядов совпадают, поэтому дипольный момент молекулы p равен нулю. В электрическом поле неполярная молекула за счет смещения ее положительных и отрицательных зарядов приобретает
индуцированный дипольный момент Pинд (пропорциональный
вектору E электрического поля |
|
p инд = α ε 0 E , |
(2.54) |
где α – скалярная величина, называемая поляризуемостью молекулы.
ПОЛЯРИЗУЕМОСТЬ атомов, ионоз, молекул, - способность этих частиц приобретать дипольный момент p в электрич. поле. Появление m обусловлено смещением электронов (электронная П.) и атомных ядер (атомная П.) под действием поля; такой наведенный (индуцированный) дипольный момент исчезает при выключении поля. У полярных молекул,обладающих постоянным дипольным моментом в отсутствие поля, наведенный дипольный момент векторно складывается с постоянным.
Поляризация |
диэлектриков — |
явление, |
связанное |
с |
поляризацией |
связанных зарядов в диэлектрике и |
поворотом |
электрических диполей под |
воздействием |
||
внешнего электрического поля. Поляризацию диэлектриков характеризует вектор |
электрической |
||||
поляризации.Физический смысл: поляризованность - это дипольный момент, который приобретают полярные молекулы, в единице объема диэлектрика.
Вектором поляризации называют электрический момент единицы объема диэлектрика. Он равен векторной сумме электрических моментов всех молекул, заключенных в единице объема. В изотропном диэлектрике вектор поляризации связан с вектором напряженности следующим образом:
P=aE,
где a получила название коэффициента эректризации или диэлектрической восприимчивости данного вещества.
Диэлектрическая восприимчивость вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивостьχe — коэффициент пропорциональности между поляризованностью P среды (дипольный момент единицы объёма) и напряженностью E внешнего электрического поля:
В системе СИ:
где  — электрическая постоянная. В случае вакуума
— электрическая постоянная. В случае вакуума
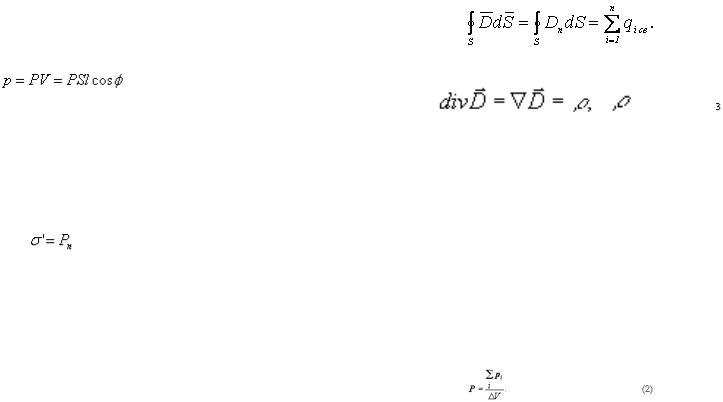
У диэлектриков, как правило, диэлектрическая восприимчивость положительна.
В системе СИ диэлектрическая восприимчивость является безразмерной величиной.
13) Поле в диэлектрике является суперпозицией полей Eстор, (созданного зарядами, входящими в пределы диэлектрика но не в состав его молекул и расположенными за его пределами) и поле Есвяз (созд. Связанными зарядами). Получившееся поле называется микроскопическим или истинным. Емикро = Естор + Есвяз = Е0 + Е’ Где Е0 – усредненное поле сторонних зарядов; Е’ – усредненное поле связанных зарядов Пусть Р- вектор поляризации,а р – электрический элемент одной молекулы, тогда
(т.к.  – объем параллелепипеда).
– объем параллелепипеда).
Приравняем и учтем, что  – проекция
– проекция 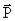 на направление
на направление  – вектора нормали, тогда
– вектора нормали, тогда
Поверхностная плотность поляризационных зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности.
Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные
заряды, объемная плотность которых  .
.
14) Теорема Гаусса для электростатического поля в диэлектрике формулируется
следующим образом: поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов, т.е.
теорема Гаусса - Остроградского для поля в диэлектрике, в дифференциальной
форме выглядит так: |
= dq/dV, [Кл / м ] (10) |
ρ - объемная плотность свободных зарядов.
Вектор электрической индукции D (называемый также электрическим смещением) является суммой двух векторов различной природы: напряжённости электрического поля Е — главной характеристики этого поля — и поляризации Р, которая определяет электрическое состояние вещества в этом поле.
в системе СИ D=e0E + P, (1¢)
где e0 — размерная константа, называемая электрической постоянной или диэлектрической проницаемостью вакуума. Вектор поляризации Р представляет собой электрический дипольный момент единицы объёма вещества в поле Е,т. е. сумму электрических дипольных моментов pi, отдельных молекул внутри малого объёма DV, деленную на величину этого объёма:
Диэлектрическая проницаемость,
величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле. В соотношении D = eЕ, где Е — напряжённость электрического поля, D— электрическая индукция в среде, Д. п. — коэффициент пропорциональности e. В большинстве диэлектриков при не очень сильных полях Д. п. не зависит от поля Е. В сильных электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках (например, сегнетоэлектриках) в обычных полях зависимость D от Е — нелинейная (см. Нелинейная оптика).
Величина Д. п. существенно зависит от типа вещества и от внешних условий (температуры, давления и т.п.). В переменных электрических полях Д. п. зависит от частоты поля Е (см. Диэлектрики)
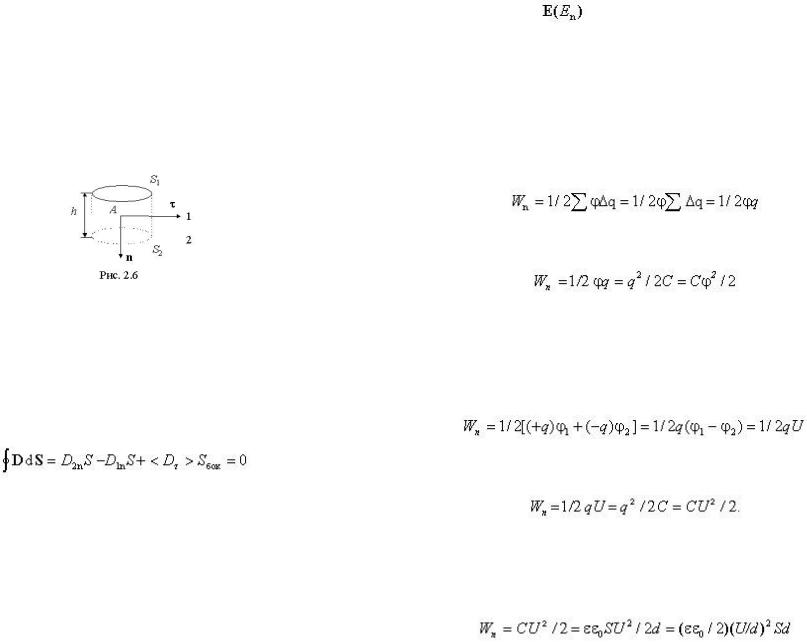
15) Граничные условия для нормальных составляющих векторов D и
E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность
в виде цилиндра, образующая которого перпендикулярна к границе раздела, а
основания находятся на равном расстоянии от границы (рис. 2.6).
Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность
 .
.
Выделяя потоки через основания и боковую поверхность цилиндра
,
где  - значение
- значение  касательной составляющей усредненное по боковой поверхности
касательной составляющей усредненное по боковой поверхности  . Переходя к пределу при
. Переходя к пределу при  (при
(при  этом также стремится к
этом также стремится к
нулю), получаем 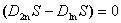 , или окончательно для нормальных составляющих вектора электрической индукции
, или окончательно для нормальных составляющих вектора электрической индукции
 .
.
 .
.
Таким образом, при переходе через границу раздела диэлектрических сред нормальная
составляющая |
вектора |
терпит разрыв, |
а |
нормальная |
составляющая |
вектора  непрерывна.
непрерывна.
16) Энергия заряженного проводника. Поверхность проводника является
эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды dq, одинаковы и равны потенциалу  проводника. Заряд q, находящийся на
проводника. Заряд q, находящийся на
проводнике, можно рассматривать как систему точечных зарядов dq. Тогда энергия
заряженного проводника
Приняв во внимание определение емкости, можно записать
Любое из этих выражений определяет энергию заряженного проводника. Энергия заряженного конденсатора. Пусть потенциал обкладки конденсатора, на
которой находится заряд +q, равен 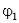 , а потенциал обкладки, на которой находится заряд -q, равен
, а потенциал обкладки, на которой находится заряд -q, равен  . Энергия такой системы
. Энергия такой системы
.
Энергию заряженного конденсатора можно представить в виде
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
Для нормальных составляющих вектора напряженности поля получим
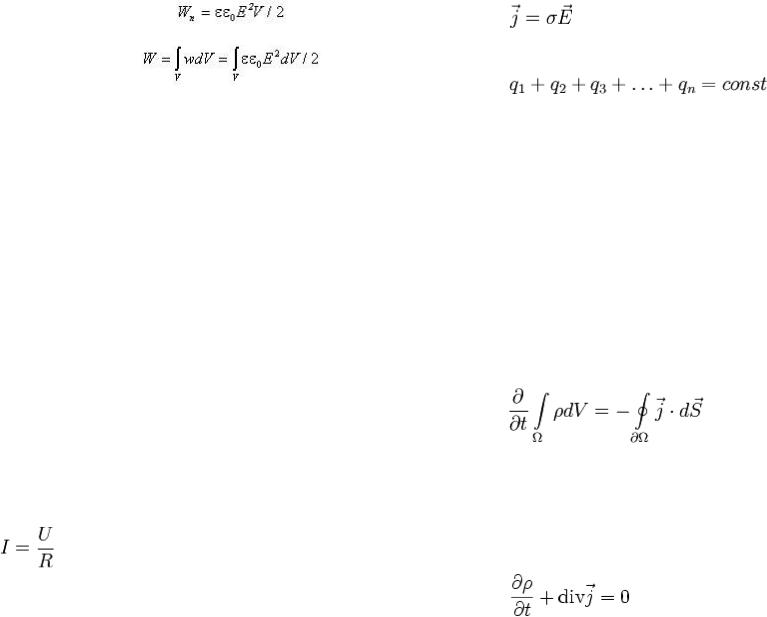
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
17.Электрический ток. Сила тока. Плотность тока. Закон сохранения электрического заряда. Уравнение непрерывности.
Электрический ток — направленное движение электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в полупроводниках — электроны и так называемые «дырки» («электронно-дырочная проводимость»).
Направление тока
Исторически принято, что направление тока совпадает с направлением движения положительного заряда в проводнике. При этом, если единственными носителями тока являются отрицательно заряженные частицы (например, электроны в металле), то направление тока противоположно направлению движения электронов.
[править] Сила и плотность тока
Основная статья: Сила тока
Силой тока называется физическая величина, равная отношению количества заряда, прошедшего за некоторое время через поперечное сечение проводника, к величине этого промежутка времени.
Сила тока в системе СИ измеряется в Амперах.
По закону Ома сила тока I пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника R:
Плотностью тока называется вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярную направлению тока, к величине этой площадки, а направление вектора совпадает с направлением движения положительного заряда в токе.
Согласно закону Ома плотность тока в среде  пропорциональна напряжённости
пропорциональна напряжённости 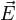 электрического поля и проводимости среды
электрического поля и проводимости среды  :
:
Плотность тока в системе СИ измеряется в амперах на квадратный метр.
Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение не известно, в частности, не известно с какой симметрией он связан[1][нет в источнике]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
Здесь Ω — некоторая произвольная область в трёхмерном пространстве, — граница этой области, ρ — плотность заряда, — плотность тока (плотность потока электрического заряда) через границу.
Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
Закон сохранения заряда в электронике
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему
