lab 5 / Лекция 5 - Аппроксимация

Линейная регрессия

Частный случай степенного многочлена:

f (x,a0 ,a1...am ) = a0 + a1 x

Для нахождения коэффициентов так же используется функция

а=polyfit(x,y,n)

при условии, что n=1

Восстановление полинома по коэффициентам

Для вычисления значений полинома f(x,а0,а1…аn) в произвольной точке необходимо использовать функцию

f=polyval (а,x)

Которой в качестве аргументов отдаются:

а – вектор коэффициентов, полученных с помощью polyfit

х – точка, в которой необходимо рассчитать значение функции

Коэффициент корреляции

Для вычисления коэффициента корреляции Пирсона между векторами x и y используется функция :

R = corrcoef(x,y)

Если R≈1 – вектора линейно зависимы, т.е. y ≈a∙x+b, a>0 Если R≈-1 – вектора линейно зависимы, y ≈a∙x+b, a<0 Если R≈0 – вектора линейно независимы, т.е. взаимосвязь между x и y – нелинейная

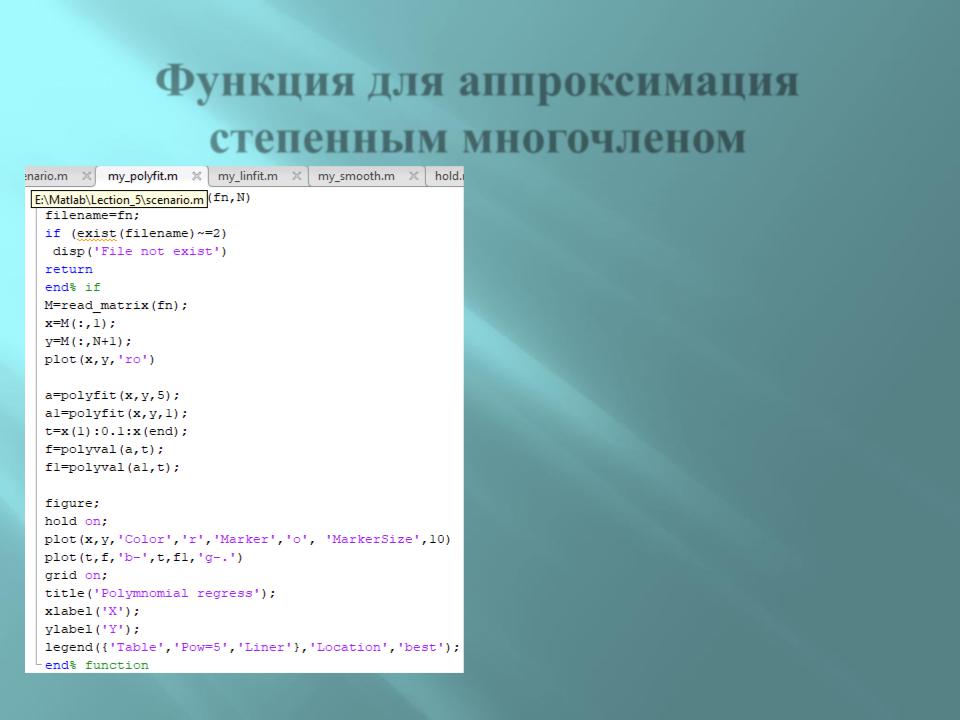
Функция для аппроксимация степенным многочленом

Проверка существования файла, выход, если его нет

Чтение из файла при помощи своей функции, Получение нужных данных в соответствии с вариантом

Аппроксимация полиномом 5 и 1 степени

Вычисление значений аппрокс. полиномов в заданных точках t

Построение графиков исх. данных и аппрокс. полиномов

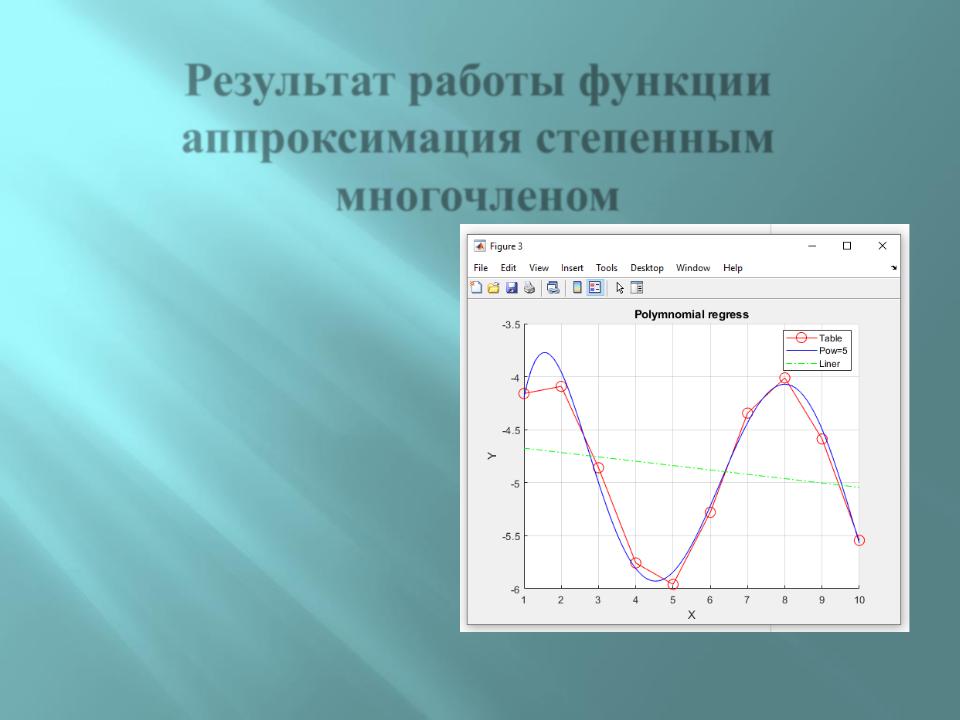
Результат работы функции аппроксимация степенным многочленом

fn=‘путь к файлу\Experiment_data_2.txt' N=1;

my_polyfit (fn,N)

Аппроксимация обобщенным многочленом

f (x,a0 ,a1...am ) = a0 0 (x)+ a1 1 (x)+... + am m (x)

Аппроксимация функцией, представляющей линейную комбинацию базисных функций φi(x), каждая из которых может быть нелинейна относительно х.

Вид базисных функций и их количество подбираются для каждого набора исходных данных индивидуально!!!!

Задание обобщенного многочлена

Для задания аппроксимационной зависимости используется функция

my_model=fittype (libMod) my_model=fittype (Eq, Name, Val)

my_model – имя модели, которое используется в дальнейшем

libMod – имя из стандартной библиотеки моделей Eq – функция, задающая аппроксимацию

Name, Val – опции, заданные в виде пары Имя опции, ее значение

Стандартная библиотека

(libMod)

Функция, задающая аппроксимацию

Примеры даны для уравнения вида: A+B*sin(x)+C*x

•Модель в виде вектора символов, что позволяет использовать .m файлы:

my_model=fittype('A+B*sin(x)+C*x')

•Модель в виде массива ячеек из символьных векторов my_model=fittype({'1','sin(x)','x’})

•Модель в виде анонимной функции

my_model=fittype(@(A,B,C,x) A+B*sin(x)+C*x)

Примечание: уравнение записываем только через х

Аргументы в виде пар

Имя, Значение