В каких сосудах системы кровообращения человека – крупных или мелких – существует большая вероятность перехода ламинарного течения крови в турбулентное?

Определить максимальное количество крови, которое может пройти через аорту за две секунды, чтобы течение сохранялось ламинарным. Диаметр аорты D=2 см, вязкость крови равна 5•10-3 Па•с, число Рейнольдса Re=2300.

0, 36 кг

Определите диаметр артерии, если через нее проходит за две секунды кровь массой 20г. Течение крови считать ламинарным. Число Рейнольдса равняется 1000. Вязкость крови принять равной 4х10-3

0,32 см

На каждый квадратный метр площади дна канала, по которому протекает вода, действует сила 0,025 мН. Определить скорость верхних слоев воды, если высотa движущегося потока воды h= 25 м, а вязкость воды 1,2·10 Па·с

0,520м/с

При остановке крови наблюдается формирование монетных столбиков – образование неупорядоченной сети агрегированных эритроцитов. Будет ли этот процесс оказывать влияние на вязкость крови? Как? увеличение вязкости

Внутреннее трение в жидкости является следствием переноса .

Какой отдел сосудистого русла обладает наибольшим гидравлическим сопротивлением

чем меньше сосуд, тем больше сопротивление

Средняя скорость кровотока в аорте составляет 0,45 м/с, а в капиллярах – 0.5 мм/с. Во сколько раз площадь поперечного сечения аорты меньше суммы поперечных сечений капилляра? Выберите один ответ: 900

На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная пропорциональны площади взаимодействующих слоев S и градиенту скорости

При протекании крови по капиллярам агрегаты эритроцитов распадаются и вязкость падает.

Задачи

1. Вывести формулу для определения вязкости ротационным вискозиметром. Дано: R, ΔR, h, ν, M.

2. Определить время протекания крови через капилляр вискозиметра, если вода протекает через него за 10 с. Объемы воды и крови одинаковы. Плотность воды и крови равны p₁ = 1 г/см³, ρ₂ = 1,06 г/см³. Вязкость крови относительно воды равна 5 (η₂/η₁ = 5).

3. Допустим, что в двух кровеносных сосудах градиент давления одинаков, а поток крови (объемный расход) во втором сосуде на 80% меньше, чем в первом. Найти отношение их диаметров.

4. Какова должна быть разность давлений АР на концах капилляра радиуса r = 1 мм и длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1 см³ воды (коэффициент вязкости η₁ = 10^-3 Пас) или глицерина (η₂ = 0,85 Пас)?

5. Падение давления в кровеносном сосуде длины L = 55 мм и радиуса r = 1,5 мм равно 365 Па. Определить, сколько миллилитров крови протекает через сосуд за 1 минуту. Коэффициент вязкости крови η = 4,5 мПа-с.

6. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое значение числа Рейнольдса может снизиться до 1160. Определить для этого случая скорость, при которой возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм. Плотность крови равна ρ = 1050 кг/м³, вязкость крови равна η = 5х10^-3 Пас.

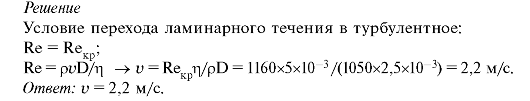7. Средняя скорость крови в аорте радиусом 1 см равна 30 см/с. Выяснить, является ли данное течение ламинарным? Плотность крови ρ = 1,05х10³ кг/м³.

η = 4х10^-3 Па-с; Rе_кр = 2300.

8. При большой физической нагрузке скорость кровотока иногда увеличивается вдвое. Пользуясь данными примера задачи (7), определить характер течения в этом случае.

Решение

Re = 2x1575 = 3150. Течение турбулентное.

Ответ: число Рейнольдса больше критического значения, поэтому течение может стать турбулентным.

9. Рассчитать число Рейнольдса для течения крови в капилляре, если скорость течения равна 0,5 мм/с, а диаметр капилляра 0,1 мм. Плотность крови ρ = 1050 кг/м³, η = 4x10^-3 Па-с.

10. Определить максимальную массу крови, которая может пройти за 1 с через аорту при сохранении ламинарного характера течения. Диаметр аорты D = 2 см, вязкость крови η = 4x10^-3 Па-с.

11. Определить максимальную объемную скорость протекания жидкости по игле шприца с внутренним диаметром D = 0,3 мм, при которой сохраняется ламинарный характер течения.

12. Найти объемную скорость жидкости в игле шприца. Плотность жидкости - ρ; ее вязкость - η; диаметр и длина иглы D и L соответственно; сила, действующая на поршень, - F; площадь поршня - S.

Интегрируя по r, получим:

Пусть поршень шприца движется под действием силы F со скоростью u. Тогда мощность внешней силы N_F = Fu.

Суммарная работа всех сил равна изменению кинетической энергии. Следовательно,

Подставив найденное значение AP во второе уравнение, получим все интересующие нас величины: скорость поршня и, объемную скорость кровотока Q, скорость жидкости в игле v.