
1курс 2сем / ЛР2 физика
.docx

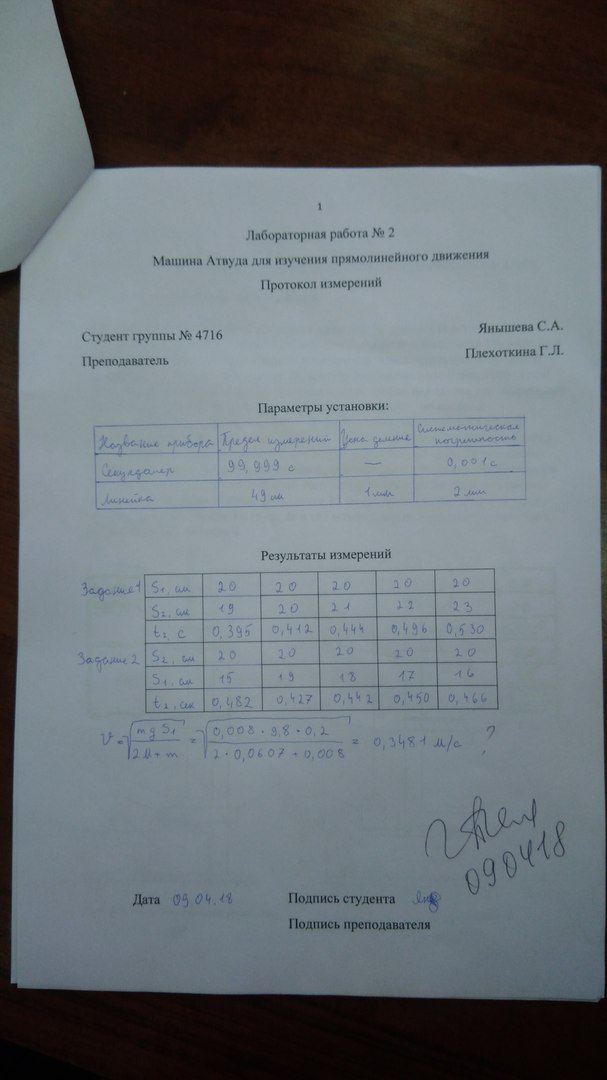
1. Цель работы.
Исследование равномерного и равноускоренного прямолинейного движения.
2. Описание лабораторной установки.
Рисунок
1. Схема лабораторной установки
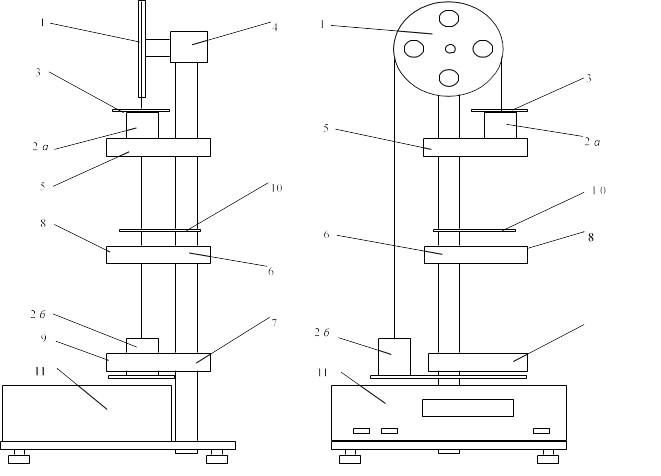 нешний
вид лабораторной установки приведен
на рис. 1. На вертикальной стойке закреплен
блок 1, через который проходит нить с
большими грузами 2а и 2б. На правый груз
2а сверху может помещаться дополнительный
небольшой грузик кольцо 3. Электромагнит
4 фиксирует начальное положение грузов
при помощи фрикционной муфты. На
вертикальной стойке находятся три
подвижных кронштейна 5, 6 и 7. Верхний
кронштейн 5 имеет риску, по которой
устанавливается низ большого груза.
Для измерения расстояний на стойке
нанесена миллиметровая шкала. Средний
6 и нижний 7 кронштейны снабжены
фотоэлектрическими датчиками 8 и 9. Когда
нижний край груза 2а пересекает оптическую
ось верхнего фотодатчика 8, включается
секундомер. Выключается он в тот момент,
когда нижний край того же груза пересекает
оптическую ось фотодатчика 9. Дополнительная
полочка 10 на среднем кронштейне 6 снимает
дополнительный грузик 3 с груза 2а в тот
момент, когда последний пересекает
оптическую ось датчика 8.
нешний
вид лабораторной установки приведен
на рис. 1. На вертикальной стойке закреплен
блок 1, через который проходит нить с
большими грузами 2а и 2б. На правый груз
2а сверху может помещаться дополнительный
небольшой грузик кольцо 3. Электромагнит
4 фиксирует начальное положение грузов
при помощи фрикционной муфты. На
вертикальной стойке находятся три
подвижных кронштейна 5, 6 и 7. Верхний
кронштейн 5 имеет риску, по которой
устанавливается низ большого груза.
Для измерения расстояний на стойке
нанесена миллиметровая шкала. Средний
6 и нижний 7 кронштейны снабжены
фотоэлектрическими датчиками 8 и 9. Когда
нижний край груза 2а пересекает оптическую
ось верхнего фотодатчика 8, включается
секундомер. Выключается он в тот момент,
когда нижний край того же груза пересекает
оптическую ось фотодатчика 9. Дополнительная
полочка 10 на среднем кронштейне 6 снимает
дополнительный грузик 3 с груза 2а в тот
момент, когда последний пересекает
оптическую ось датчика 8.
Параметры установки.
Таблица 2.1
Название прибора |
Предел измерений |
Систематическая погрешность |
Цена деления |
Секундомер (циф.) |
99,999 с |
0,001 с |
- |
Линейка |
49 см |
2 мм |
1 мм |
Масса груза 1 = 1884г.
Масса груза 2 = 1968г.
θT = 0,0005c.
3. Рабочие формулы.
Формулы вычисления ускорения:
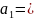
 (1)
(1)
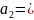
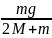 (2)
(2)
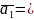
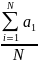 (3)
(3)
a1
– ускорение
грузов на участке S1,
a2
– расчетное ускорение системы грузов,
S1
– путь, пройденный телами с ускорением
a1,
S2
– путь, пройденный телами за время t2,
M
– масса грузика, m
– масса дополнительного грузика
(кольцо),
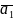 – среднее значение ускорения на участке
S1,
g
– ускорение свободного падения (~9,8
м/с2),
N
– количество измерений.
– среднее значение ускорения на участке
S1,
g
– ускорение свободного падения (~9,8
м/с2),
N
– количество измерений.
Формулы вычисления скоростей:
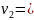
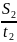 (4)
(4)
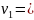
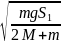 (5)
(5)
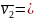
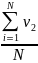 (6)
(6)
v1 – расчетная скорость при переходе с равноускоренного движения на равномерное, v2 – экспериментальная скорость равномерного движения грузов,
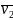 – среднее значение
скорости при переходе с равноускоренного
движения на равномерное.
– среднее значение
скорости при переходе с равноускоренного
движения на равномерное.
Результаты измерений и вычислений.
Результаты измерений и вычисления данных для дальнейшего анализа
Таблица 4.1
S2, м |
0,19 |
0,20 |
0,21 |
0,22 |
0,23 |
t2, с |
0,395 |
0,412 |
0,444 |
0,496 |
0,530 |
v2, м/с |
0,48 |
0,49 |
0,47 |
0,47 |
0,47 |
а1, м/с2 |
0,58 |
0,59 |
0,56 |
0,57 |
0,57 |
S1 = 0,2 м
V2 = 0,48 м/с
V1 = 0,34 м/с
Пример расчетов по рабочим формулам.
По
формуле (1) a1
=
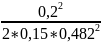 = 0,574 м/с2
= 0,574 м/с2
По
формуле (2) a2
=
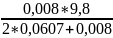 = 0,606 м/с2
= 0,606 м/с2
По
формуле (3)
=
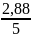 = 0,576 м/с2
= 0,576 м/с2
По
формуле (4) v2
=
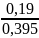 =
0,481 м/с
=
0,481 м/с
По
формуле (5) v1
=
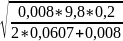 = 0,348 м/с
= 0,348 м/с
По
формуле (6)
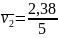 = 0,476 м/с
= 0,476 м/с
Вывод формулы и расчет погрешностей.
Вывод формулы систематической погрешности.

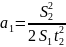
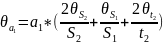
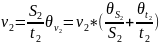
Расчёт погрешности по выведенной формуле.
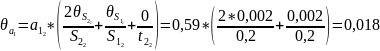 м/с2
м/с2
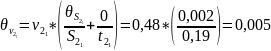 м/с
м/с
Случайные погрешности
6.3.1 Средняя квадратичная погрешность отдельного измерения ускорения.
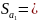
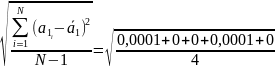 = 0,007 м/с2
= 0,007 м/с2
6.3.2 Среднее квадратичное отклонение ускорения.
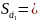
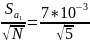 =
0,003 м/с2
=
0,003 м/с2
6.3.3 Средняя квадратичная погрешность отдельного измерения скорости.
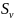 =
=
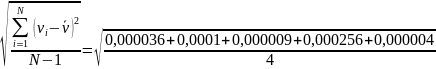 =
=
 0,001
м/с
0,001
м/с
6.3.4 Среднее квадратичное отклонение скорости.
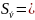
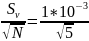 =
0,004 м/с
=
0,004 м/с
В
этой работе производится измерение
неслучайных по своей природе физических
величин: скорость движения и ускорения
грузов, поэтому случайные погрешности
определяются только влиянием приборных
ошибок на измеряемые величины. В этом
случае должны выполняться неравенства:
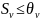 ;
;
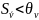 . Лучше, если
первое из неравенств будет строгим, а
второе нестрогим:
. Лучше, если
первое из неравенств будет строгим, а
второе нестрогим:
0,001 < 0,005 т.е
0,004 < 0,005 т.е
Получившиеся неравенства говорят о том, что в измерениях, скорее всего, нет грубых ошибок и промахов.
Вывод: Установила, что движение на участке S1 является равноускоренным, а на участке S2 – равномерным. Определила экспериментальное ускорение грузов и расчетное значение: а1 = (0,574 ± 0,018) м/с2, а2 = (0,606 ± 0,018) м/с2. Определила скорости грузов и расчетное значение: V2 = (0,481 ± 0,005) м/с, V1 = (0,348 ± 0,005) м/с.
|aэкс
– aтеор|
<
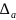 |Vэкс
– Vтеор|
<
|Vэкс
– Vтеор|
<
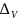
|0,007 м/с2 – 0,003 м/с2 | < 0,02 м/с2 |0,004 м/с – 0,001 м/с | < 0,005 м/с
|0,004 м/с2 | < 0,02 м/с2 |0,003 м/с | < 0,005 м/с
Получившиеся неравенства говорят о том, что в измерениях, нет грубых ошибок и промахов.
