Обработка результатов физика 1 лаба
.docxЗадание по обработке результатов
-
Статистическая обработка измеренных значений. Определить по данным таблиц 1 и 2 средние значения интервалов времени
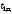 ,
,
 ,
,
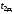 и
и
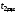 .
Определить погрешности этих величин
с доверительной вероятностью P
= 95%.
.
Определить погрешности этих величин
с доверительной вероятностью P
= 95%.
Таблица 1
|
N |
1 |
2 |
3 |
4 |
5 |
|
|
9,51 |
9,35 |
9,51 |
9,33 |
9,49 |
|
|
13,53 |
13,3 |
13,29 |
13,56 |
13,52 |
|
|
37,76 |
39,21 |
37,28 |
38,37 |
37,85 |
|
|
44,3 |
44,82 |
45,32 |
44,13 |
43,89 |
Определим средние значения
 ,
,
 :
:




Формула расчета СКО

Формула случайной доверительной
погрешности результата измерений

Приборная погрешность





Полные погрешности результатов измерений
вычисляются по формуле
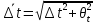 и равны:
и равны:



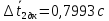
Значит,
 ,
,
 равны:
равны:
 с
с



Сведем все вычисленные значения в Таблицу 2
Таблица 2
|
Среднее значения величины, с |
Результат, с |
|
|
|
|
|
|
|
|
|
|
|
|
-
Определение периода колебаний маятника. Пользуясь методом переноса погрешностей, для диска без кольца и с кольцом рассчитайте средние значения и полные погрешности периода колебаний

 .
.
Проведем расчеты для диска без кольца:
Расчетная формула
 ,
где n=10.
,
где n=10.
Пользуясь значениями, найденными в пункте 1 (Таблица 2), вычислим

Полная погрешность
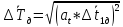 ,
где
,
где


Значит, среднее значение периода
колебания диска без кольца
 ,
а полная погрешность периода колебаний
составляет 0,0015 с
,
а полная погрешность периода колебаний
составляет 0,0015 с
 с
с
Проведем расчеты для диска с кольцом:
Расчетная формула
 ,
где n=10.
,
где n=10.
Пользуясь значениями, найденными в пункте 1 (Таблица 2), вычислим
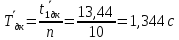
Полная погрешность
 ,
где
,
где

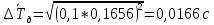
Значит, среднее значение периода
колебания диска с кольцом
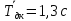 ,
а полная погрешность периода колебаний
составляет 0,2 с.
,
а полная погрешность периода колебаний
составляет 0,2 с.

3. Определение момента инерции маятника. Определить момент инерции маятника по формуле
 ,
,
 ,
,
где
 – момент инерции кольца. Вычислить
погрешность
– момент инерции кольца. Вычислить
погрешность
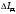 ,
пользуясь правилами расчета погрешностей
косвенных измерений. Рассчитать значение
момента инерции диска маятника, исходя
из его размеров и плотности материала.
Сравнить полученный результат с
экспериментальным значением.
,
пользуясь правилами расчета погрешностей
косвенных измерений. Рассчитать значение
момента инерции диска маятника, исходя
из его размеров и плотности материала.
Сравнить полученный результат с
экспериментальным значением.
Пользуясь расчетами пунктов 1 и 2 определим
среднее значение момента инерции
маятника
 ,
которое рассчитывается по формуле
,
которое рассчитывается по формуле


Погрешность измерений момента инерции
равна
 .
.

Произведем расчет инерции диска маятника,
исходя из его размеров и плотности
материала. Расчетная формула
 ,
где
,
где
 – плотность материала,
– плотность материала,
 - толщина диска маятника,
- толщина диска маятника,
 - диаметр диска маятника
- диаметр диска маятника

4. Определение времени затухания маятника. Пользуясь методом переноса погрешностей, для диска без кольца и с кольцом рассчитайте средние значения и полные погрешности времени затухания маятника и погрешность при P = 95%. Время затухания вычисляется по формуле
 .
.
Определим время затухания маятника без кольца
Воспользуемся значениями
 и
и
 ,
расчитаными в пункте 1 (Таблица 2)
,
расчитаными в пункте 1 (Таблица 2)
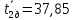

Рассчитаем среднее значение времени
затухания маятника


Полная погрешность времени затухания
маятника без кольца вычисляется по
формуле


Значит, время затухания маятника без
кольца равно
 с
с
Определим время затухания маятника с кольцом
Воспользуемся значениями
 и
и
 ,
расчитаными в пункте 1 (Таблица 2)
,
расчитаными в пункте 1 (Таблица 2)


Рассчитаем среднее значение времени
затухания маятника

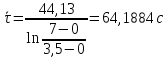
Полная погрешность времени затухания
маятника с кольцом вычисляется по
формуле


Значит, время затухания маятника с
кольцом равно
 с
с
5. Определение собственной частоты
колебаний гармонического осциллятора.
Пользуясь выражениями
 и
и
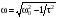 ,
определить собственные частоты
,
определить собственные частоты
 и
и
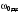 колебаний для диска без кольца и с
кольцом. Вычислить их погрешности.
колебаний для диска без кольца и с
кольцом. Вычислить их погрешности.
Собственные частоты
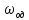 и
и
 можно вычислить по формуле
можно вычислить по формуле

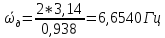

![]()
 =
6,6539 Гц
=
6,6539 Гц
 =
4,6726 Гц
=
4,6726 Гц
Погрешность

Погрешность
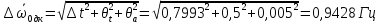


6. Определение коэффициента
кручения и модуля сдвига материала
подвеса. Найти коэффициент кручения
 и погрешность k.
Рассчитать среднее значение модуля
сдвига G.
и погрешность k.
Рассчитать среднее значение модуля
сдвига G.
Коэффициент кручения можно рассчитать
по формуле




Рассчитаем модуль сдвига
 ,
где l – длина подвеса,
а d – диаметр подвеса
,
где l – длина подвеса,
а d – диаметр подвеса
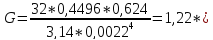 1011 1/м3
1011 1/м3
7. Определение полной энергии, мощности потерь и добротности маятника. Пользуясь соответствующими соотношениями, определить средние значения указанных величин.
Полная энергия маятника W
рассчитывается по формуле
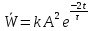 ,
где A – конечная амплитуда
,
где A – конечная амплитуда

Мощность потерь
 расчитывается по формуле
расчитывается по формуле


Добротность маятника
 расчитывается по формуле
расчитывается по формуле
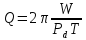
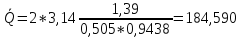 Дж
Дж
8. В соответствии с уравнением затухающих колебаний построить графики зависимости угла сдвига и амплитуды колебаний от времени для одного из наблюдений.
9. Графики


Вывод:
Выполнив данную лабораторную работу, мы провели исследование динамики колебательного движения крутильного маятника, и получили такие значения :
 с ω0д=7±1 Гц
с ω0д=7±1 Гц
Tдк=1,344±0,017 с ω0дк=4,7±0,9 Гц
 k=0,449±0,013
k=0,449±0,013

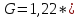 1011 1/м3
1011 1/м3





 ,
c
,
c ,
c
,
c ,
c
,
c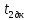 ,c
,c