дз2фкп
.docx
|
Министерство науки и высшего образования Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана (Национальный Исследовательский Университет)» (КФ МГТУ им. Н.Э. Баумана) |
ФАКУЛЬТЕТ |
М-КФ «Машиностроительный» |
КАФЕДРА |
М10-КФ «Высшая математика» |
ДОМАШНЯЯ РАБОТА №2
Вариант 19
ДИСЦИПЛИНА: |
"Функции комплексной переменой" |
ТЕМА: |
"Функции комплексной переменой" |
Выполнил: студент гр. ИУК1-31Б |
_ Подпись Ф.И.О.
|
Проверил: |
_______________(Беляев В. А. ) Подпись Ф.И.О.
|
Дата сдачи (защиты): |
|
|
Результаты сдачи (защиты):
-Балльная оценка
-Оценка |
|
|
|
|
|
Калуга, 2020 г.
Задача №1
Найдите
круг и радиус сходимости степенного
ряда
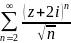 ,
исследуйте сходимость ряда в точках
,
исследуйте сходимость ряда в точках
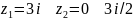 .
.
Решение:
Рассмотрим
ряд модулей членов данного ряда, т.е.
ряд
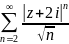 .
.
К последнему ряду применим теорему Коши.
Имеем
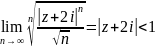 .
.
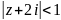 – круг
сходимости степенного ряда с центром
в точке
– круг
сходимости степенного ряда с центром
в точке
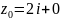 и радиусом
и радиусом
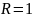 .
.
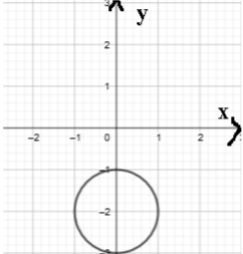
В
точке
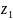 ряд расходится, т.к. точка лежит вне
круга сходимости.
ряд расходится, т.к. точка лежит вне
круга сходимости.
В
точке
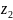 ряд расходится, т.к. точка лежит вне
круга сходимости.
ряд расходится, т.к. точка лежит вне
круга сходимости.
В
точке
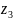 ряд расходится, т.к. точка лежит вне
круга сходимости
ряд расходится, т.к. точка лежит вне
круга сходимости
Задача №2
Найдите
круг и радиус сходимости степенного
ряда
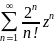 ,
исследуйте сходимость ряда в точках
,
исследуйте сходимость ряда в точках
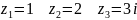 .
.
Решение:
Рассмотрим
ряд, составленный из модулей членов
данного ряда, т.е. ряд
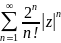 .
.
К
последнему ряду применим признак
Даламбера. Для этого найдём предел
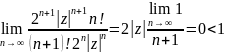 .
.
Следовательно
данный ряд сходится абсолютно в каждой
точки комплексной плоскости,
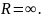
Задача №3
Дана
функция
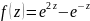 .
Выделить действительную и мнимую части
функции и проверить выполнение условия
Коши-Римана. Если возможно, то найти
производную данной функции.
.
Выделить действительную и мнимую части
функции и проверить выполнение условия
Коши-Римана. Если возможно, то найти
производную данной функции.
Решение:
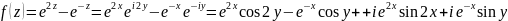
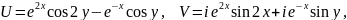
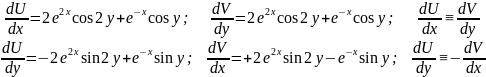
Функции
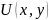 и
и
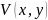 вместе с частными производными первого
порядка непрерывны во всей комплексной
плоскости.
вместе с частными производными первого
порядка непрерывны во всей комплексной
плоскости.
Условия
Коши-Римана
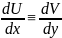 ,
,
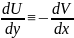 выполняются во всей комплексной
плоскости.
выполняются во всей комплексной
плоскости.
Поэтому
данная функция дифференцируема в каждой
точке комплексной плоскости. Производную
функции можно найти по формуле:
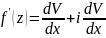
Имеем:
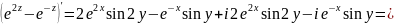
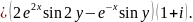
Задача №4
Решить
дифуравнение
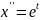 ,
,
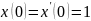 операционным методом.
операционным методом.
Решение:


 ______________(Прудников
А. Ф.)
______________(Прудников
А. Ф.)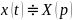 ,
тогда
,
тогда
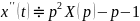 ,
,
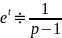 .
.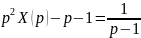
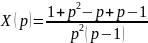
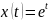 .
.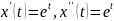
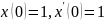
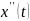 в исходное уравнение.
в исходное уравнение.