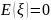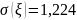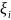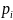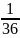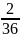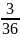ДЗ1
.docx
 Министерство
науки и высшего образования Российской
Федерации
Министерство
науки и высшего образования Российской
Федерации
Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Московский государственный технический университет имени Н.Э. Баумана
(Национальный Исследовательский Университет)»
(КФ МГТУ им. Н.Э. Баумана)
ФАКУЛЬТЕТ |
М-КФ «Машиностроительный» |
КАФЕДРА |
М10-КФ «Высшая математика» |
ДОМАШНЯЯ РАБОТА №1
ДИСЦИПЛИНА: |
«Теория вероятностей и математическая статистика» |
|
ТЕМА: |
«Основные понятия теории вероятностей» |
|
|
|
|
Выполнил: студент гр. ИУК1-41Б |
_______________(Прудников А.Ф.) Подпись Ф.И.О.
|
Проверил: |
_______________(Савотин А.И.) Подпись Ф.И.О.
|
Дата сдачи (защиты): |
|
|
Результаты сдачи (защиты):
-Балльная оценка
-Оценка |
|
|
|
|
|
Калуга, 2021 г.
Задание №1
Вероятность того, что выстрел попадет в цель, равна p=0,66. Сколько нужно сделать выстрелов, чтобы вероятность хотя бы одного попадания была больше заданного значения δ=0,99.
Решение:
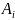 -
выстрел
попадает в цель
-
выстрел
попадает в цель
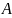 – одно
попадание при n
выстрелах.
– одно
попадание при n
выстрелах.
Рассмотрим:
 – ни одного попадания в цель при всех
выстрелах
– ни одного попадания в цель при всех
выстрелах
: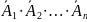
Тогда
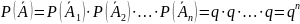 ,
где q=1-p.
,
где q=1-p.
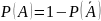 ,
т.е.
,
т.е.
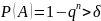 .
Отсюда
.
Отсюда
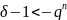
Умножим
на -1 и выразим
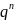 .
.
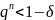
Подберём n:
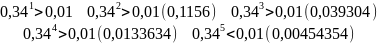
Отсюда получаем ответ, что нужно сделать 5 выстрелов, чтобы вероятность хотя бы одного попадания была больше заданного значения δ=0,99.
Ответ: 5.
Задание №2
На
некоторое обслуживающее устройство
поступают две заявки. Каждая может
поступить любой момент времени в течении
T=150
минут.
Время обслуживания заявки
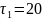 минут, второй
минут, второй
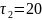 минут. При поступлении заявки на занятое
устройство она не принимается. При
поступлении заявки даже в последний
момент времени T,
она обслуживается. Найти вероятность
того, что:
минут. При поступлении заявки на занятое
устройство она не принимается. При
поступлении заявки даже в последний
момент времени T,
она обслуживается. Найти вероятность
того, что:
А) Обе заявки будут обслужены
Б) Будет обслужена ровно одна заявка
Решение:
А – обе заявки будут обслужены
В – всего одна заявка будет обслужена
Так
как на устройство не может не поступить
ни одной заявки, то исходы А и В являются
противоположными, значит В можно будет
найти из выражения
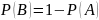 .
.
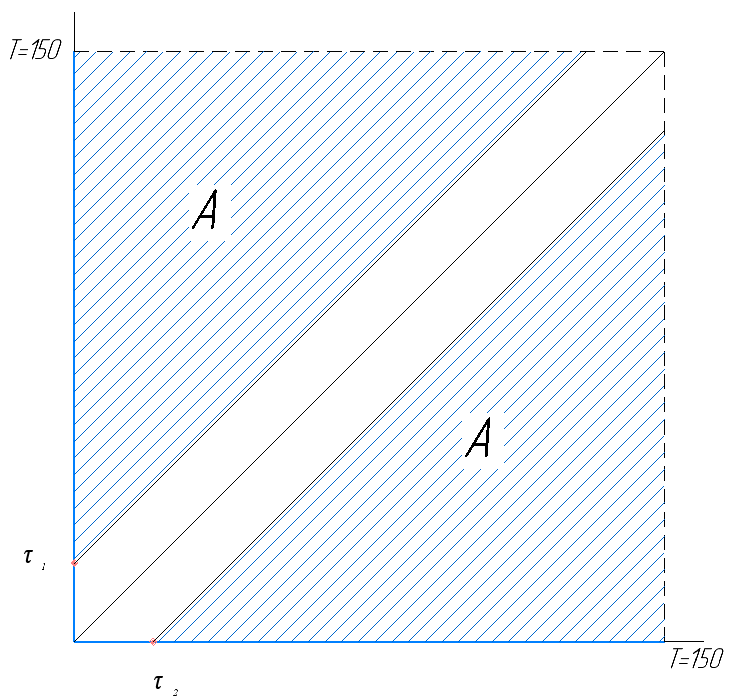
Рисунок 1
Множество благоприятных исходов А закрашено синим цветом и представляет собой объединение двух треугольников
При
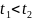 это треугольник
это треугольник
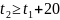 ;
;
При
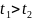 это треугольник
это треугольник
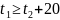 ;
;
Площадь области А равна сумме площадей этих двух треугольников:

Найдём вероятность события А:
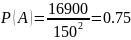
Это и будет ответ на задание а).
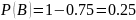
Это ответ на задание б).
Ответ:
а)
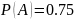 ;
б)
;
б)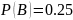 .
.
Задание №3
Задана
структурная схема надёжности, состоящая
из пяти элементов. Событие
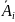 – отказ i-того
элемента за некоторый промежуток
времени. Вероятности безотказной работы
заданы:
– отказ i-того
элемента за некоторый промежуток
времени. Вероятности безотказной работы
заданы:
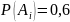 (при i=1,
3, 5) и
(при i=1,
3, 5) и
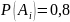 (при i=2,
4). Все события
независимы в совокупности. Событие
состоит в безотказной работе всех всей
системы за рассмотренный промежуток
времени. Требуется:
(при i=2,
4). Все события
независимы в совокупности. Событие
состоит в безотказной работе всех всей
системы за рассмотренный промежуток
времени. Требуется:
А) выразить событие через или (i=1, 2, 3, 4, 5);
Б)
найти
вероятность
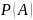 безотказной работы системы.
безотказной работы системы.
Решение:
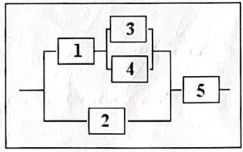
Рисунок 2
А)
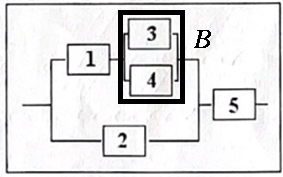
Рисунок 3 – Область А
Область
В
состоит из элементов
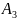 и
и
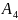 и т.к. элементы соединены параллельно,
то её вероятность безопасной работы
будет следующей:
и т.к. элементы соединены параллельно,
то её вероятность безопасной работы
будет следующей:
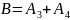
Рисунок
4 – Область С
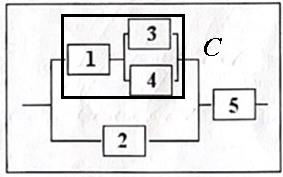 Область
С
состоит из элементов
Область
С
состоит из элементов
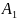 и
и
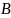 и т.к. элементы соединены последовательно,
то её вероятность безопасной работы
будет следующей:
и т.к. элементы соединены последовательно,
то её вероятность безопасной работы
будет следующей:
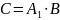
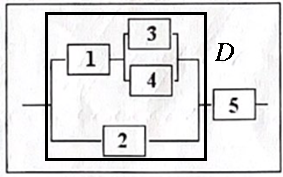
Рисунок 5 - Область D
Область
D
состоит из элементов
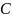 и
и
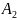 и т.к. элементы соединены параллельно,
то её вероятность безопасной работы
будет следующей:
и т.к. элементы соединены параллельно,
то её вероятность безопасной работы
будет следующей:

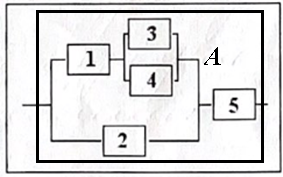
Рисунок 6 - Область А
Область
A
состоит из элементов
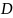 и
и
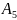 и т.к. элементы соединены последовательно,
то её вероятность безопасной работы
будет следующей:
и т.к. элементы соединены последовательно,
то её вероятность безопасной работы
будет следующей:
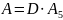
Раскроем все буквенные значения и таким выразим через :
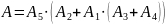
Б)
При вычислении
будем пользоваться независимостью
событий
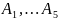 :
:
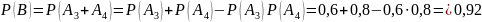 ;
;
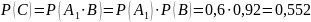 ;
;
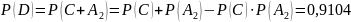 ;
;
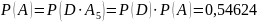 ;
;
Ответ:
А)
;
Б)
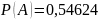 .
.
Задание №4
Из
партии, содержащей
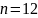 изделий, среди которых
изделий, среди которых
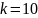 – высшего сорта, для контроля выбирают
наугад
– высшего сорта, для контроля выбирают
наугад
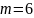 изделий. Найти вероятность того, что
среди выбранных изделий ровно
изделий. Найти вероятность того, что
среди выбранных изделий ровно
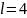 изделий высшего сорта, при условии, что
выборка производится
изделий высшего сорта, при условии, что
выборка производится
А) с возвращением (выбранное изделие после проверки возвращается обратно в партию);
Б) без возвращения (выбранное изделие в партию не возвращается);
Решение:
А)
Для нахождения события
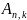 воспользуемся формулой Бернулли:
воспользуемся формулой Бернулли:
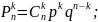
В
нашем случае независимое число испытаний
–
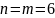 ,
а количество наступления события А
-
,
а количество наступления события А
-
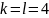 .
Найдём вероятность попадания изделия
высшего сорта из всех изделий
.
Найдём вероятность попадания изделия
высшего сорта из всех изделий
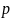 и обратную ей величину q:
и обратную ей величину q:
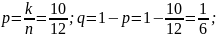
Вычислим
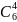 :
:

Подставим все полученные значения в начальную формулу:
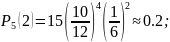
Б)
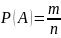 ,
,
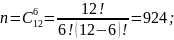
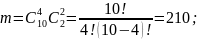
Подставим в начальное уравнение:
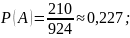
Ответ:
а)
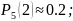 б)
б)
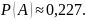
Задание №5
Вероятность
успешной сдачи экзамена на получение
водительских прав равна
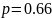 .
Найдите вероятность того, что в группе
.
Найдите вероятность того, что в группе
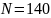 претендентов экзамен сдадут не менее
претендентов экзамен сдадут не менее
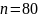 человек.
человек.
Решение:
Требуется
найти вероятность того, что из 140 человек
сдадут
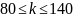 .
Вероятность высчитаем из интегрального
приближенного уравнения Лапаса:
.
Вероятность высчитаем из интегрального
приближенного уравнения Лапаса:
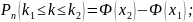
Где
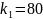 ,
а
,
а
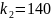 .
Найдём
.
Найдём
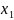 и
и
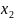 по формуле:
по формуле:
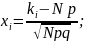
Где
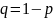 .
.
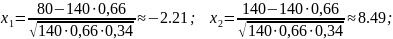
Т.к.
функция Лапласа чётная, то
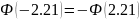 .
.
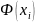 будем
искать в таблице значений функции
Лапласа. Т.о.
будем
искать в таблице значений функции
Лапласа. Т.о.
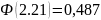 .
.
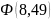 в таблице отсутствует, поэтому вычислим
её:
в таблице отсутствует, поэтому вычислим
её:
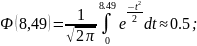
Подставим получившиеся выражения в начальное уравнение:
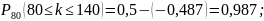
Ответ:
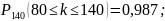
Задание №6
В
отдел технического контроля поступает
партия, содержащая
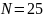 изделий, среди которых имеются
изделий, среди которых имеются
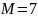 бракованных. Контролёр для контроля
отбирает 3 изделия, при этом в бракованном
изделии он обнаруживает брак с вероятностью
бракованных. Контролёр для контроля
отбирает 3 изделия, при этом в бракованном
изделии он обнаруживает брак с вероятностью
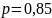 .
Партия бракуется, если среди трёх
отобранных для проверки обнаружится
хотя бы одно бракованное изделие. Найти
вероятность того, что данная партия
изделий будет забракована.
.
Партия бракуется, если среди трёх
отобранных для проверки обнаружится
хотя бы одно бракованное изделие. Найти
вероятность того, что данная партия
изделий будет забракована.
Решение:
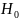 – среди
выбранных трёх изделий нет бракованных.
– среди
выбранных трёх изделий нет бракованных.
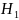 – среди
выбранных трёх изделий одно бракованное.
– среди
выбранных трёх изделий одно бракованное.
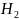 – среди
выбранных трёх изделий два бракованных.
– среди
выбранных трёх изделий два бракованных.
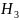 – среди
выбранных трёх изделий три бракованных.
– среди
выбранных трёх изделий три бракованных.
– данная партия будет забракованная.
– данная партия будет забракованная.
– все три изделия будут забракованы.

Отсюда
найдём
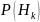 :
:
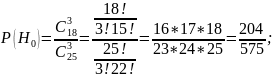
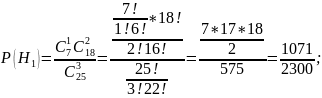
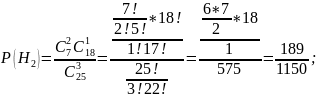
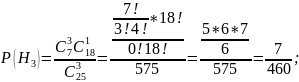
Найдём
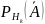 :
:
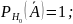
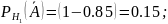
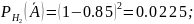
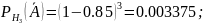
Подставим полученные значения в начальное уравнение:
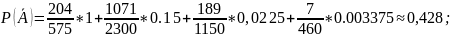
Тогда будет равна:
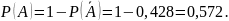
Ответ:
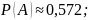
Задание №7
Одновременно подбрасывают две игральные кости; x – число очков на первом кубике, y – на втором. Для заданной в каждом варианте функции
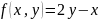 найдите:
а) закон распределения случайной величины
найдите:
а) закон распределения случайной величины
 ;
б) математическое ожидание
;
б) математическое ожидание
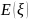 ;
в) дисперсию
;
в) дисперсию
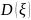 и стандартное отклонение
и стандартное отклонение
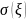 .
.
Решение:
а)
Для составления закона распределения составим таблицу
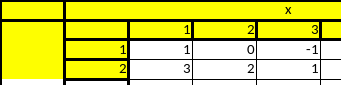
Закон
распределения случайной величины
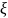 :
:
|
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для наглядности нарисуем полигон вероятностей:
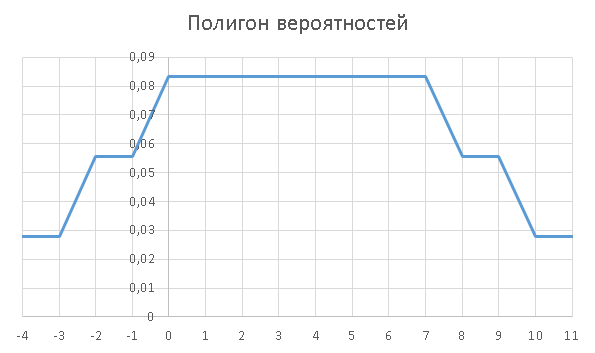
б) Математическое ожидание:

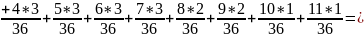
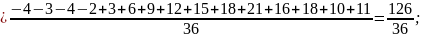
в) Дисперсия случайной величины и :
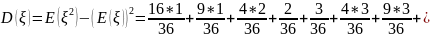
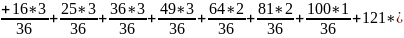
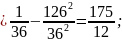
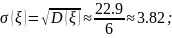
Ответ:
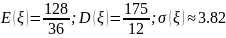
Задание №8
Непрерывная случайная величина имеет плотность распределения вероятностей
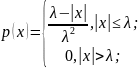
а)
Постройте график плотности распределения
вероятностей
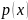 .
.
б)
Найдите функцию распределения
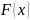 и построить её график.
и построить её график.
в)
Вычитайте вероятность попадания
случайной величины в интервал
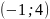 .
.
г) Найдите математическое ожидание, дисперсию и среднеквадратическое отклонение.
Решение:
а)
Данный график образуется из двух других:
на интервале
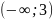 – ось ОХ, на отрезке
– ось ОХ, на отрезке
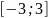 – ломанная кривая, а в интервале
– ломанная кривая, а в интервале
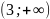 ось ОХ:
ось ОХ:
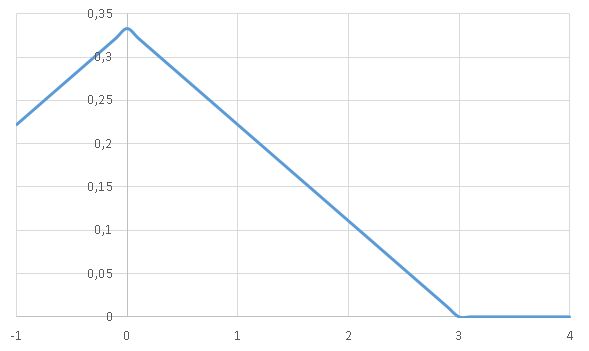
б) Чтобы вычислить вероятность выпадения случайной величины:
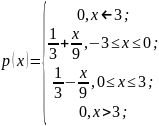
Рассмотрим все эти случаи:
Если
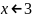 ,
то
,
то
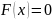 .
.Если
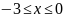 ,
то
,
то
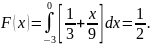
Если
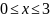 ,
то
,
то
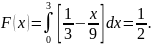
Если
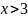 ,
то
.
,
то
.
Таким образом
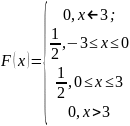
Построим :
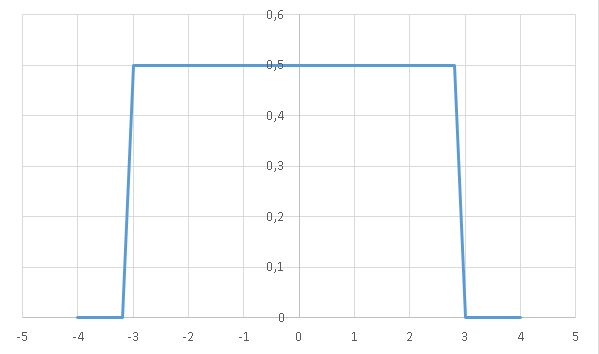
в) Чтобы вычислить вероятность попадания случайной величины в интервал воспользуемся формулой:
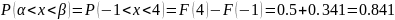
г) Найдём математическое ожидание:
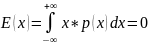 – в
силу симметричности функии относительно
оси OY.
– в
силу симметричности функии относительно
оси OY.
Дисперсию
вычислим по формуле
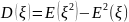 ,
поэтому найдём сначала
,
поэтому найдём сначала
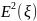 :
:
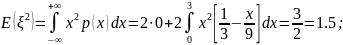
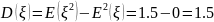 ;
;
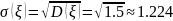 ;
;
Ответ: