§5.5. Магнитный момент атома

Из курса общей физики известно, что магнитный и орбитальный моменты электрона связаны соотношением 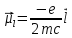. Поэтому, такое же соотношение выполняется и для операторов

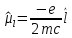. (5.31)

Знак минус показывает, что магнитный и орбитальный моменты электрона направлены в противоположные стороны. Отношение магнитного момента к орбитальному 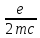называется гиромагнитным отношением.

Из релятивистской теории Дирака и эксперимента следует, что для что магнитного и спинового моментов электрона имеет место соотношение

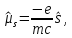(5.32)

в котором коэффициент пропорциональности в два раза, чем в выражении (5.31). Иначе говоря, спин обладает удвоенным магнетизмом.

В стационарном состоянии определенны значения могут иметь только модуль магнитного момента и его проекция на выделенную ось:

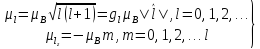(5.33)

Мы ввели в (5.33) магнетон Бора 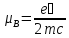= 0.92710^-20 эрг/Гс - элементарный квант магнитного момента. Для атома в (5.33) под 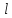надо пониматьL.

Для атомного спина:

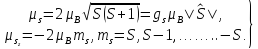(5.34)

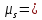
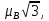
При S=1/2 m_s =1/2, -1/2, 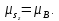Поэтому, принято говорить, что спиновый магнитный момент равен одному магнетону Бора.

Полный магнитный момент атома.

Рассмотрим

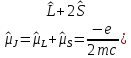). (5.35)

Отсюда следует, что вектор полного магнитного момента 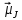и вектор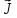- неколлинеарные векторы. Чтобы найти гиромагнитное отношение этих векторов найдем проекци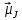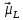и,и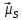на направление вектора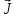. Из (5.27) получим, что

.

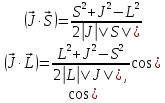В силу (5.35)

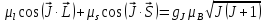. (5.36)

Подставляя сюда явные выражения для 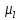и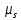из (5.33) и (5.34), получаем

= .

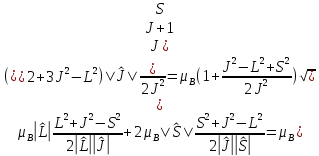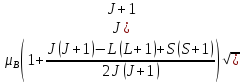Сравнивая это выражение с (5.36), получаем фактор Ланде

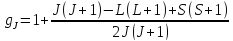. (5.37)

Теперь

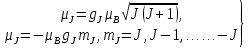(5.38)

Отметим ряд наиболее интересных случаев:

• в состоянии ⁵ 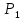фактор Ланде больше двух;

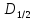
• в состоянии ⁴ 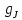=0, т.е. полный момент есть, а магнитного момента нет;

• в состоянии ⁶ 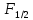фактор Ланде 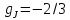отрицателен, т.е. магнитный момент направлен в ту же сторону, что и полный момент количества движения.

Глава 6. Теория возмущений

§6.1. Стационарная теория возмущений

Уравнение Шредингера решается сравнительно просто только в ряде случаев. Чаще всего установить явный вид решений стационарного уравнения Шредингера не удается. Пусть система описывается гамильтонианом 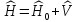, где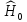 – эрмитов гамильтониан, собственные значения 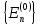и собственные функции 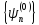которого известны, а 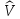есть “малая” поправка к 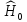или, как говорят, возмущение. Тогда для поиска собственных функций и собственных значений полного гамильтониана можно воспользоваться стационарной теорией возмущений. Оператор 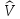может, к примеру, описывать взаимодействие системы с некоторой другой системой или с внешним полем. Если это взаимодействие является слабым, то следует ожидать, что энергетический спектр системы меняется незначительно.

Волновые функции 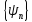и спектр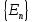возмущенной системы определяются стационарным уравнением Шредингера:

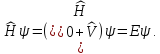(6.1)

Рассмотрим дискретный спектр и случай, когда все уровни энергии 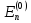не вырождены. Решение уравнения (6.1) будем искать в виде разложения по полной ортонормированной системе функций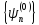, т.е.

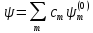(6.2)

Подставим (6.2) в (6.1), умножим обе части уравнения слева на и проинтегрируем -

.

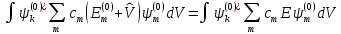Используя свойство ортонормированности функций 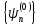, получаем

. (6.3)

Здесь 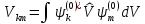– матричный элемент оператора возмущения, который считается малым. Чтобы решить (6.3), запишем:

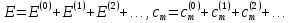(6.4)

В (6.4) 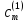,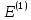- величины того же порядка малости, что и.

Первый порядок теории возмущений.

Для собственного значения E=E_n имеем:

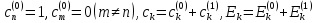(6.5)

Если k = n , то (6.3) принимает вид

,

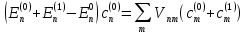откуда следует, что

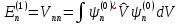. (6.6)

Если k 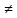n имеем

,

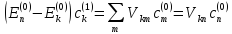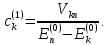(6.7)

Коэффициент 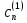выбирается так, чтобы функция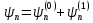была нормирована с точностью до членов первого порядка. Для этого надо положить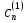=0, тогда

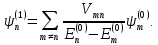(6.8)

Очевидно, что с точностью до членов первого порядка эта функция ортогональна .

Второй порядок теории возмущений.

Если k = n , то, оставляя в (6.3) только члены второго порядка малости, получаем:

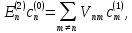
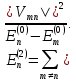(6.9)

Из (6.9) следует, что поправка второго порядка к энергии основного состояния всегда отрицательна. Кроме того, из (6.8) можно написать условие применимости теории возмущений

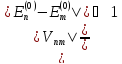(n≠m) . (6.10)

Остальные порядки теории возмущений рассматриваются аналогичным образом. Полученный ряд называется рядом Рэлея - Шредингера.