
Курсач
.docxСанкт-Петербургский государственный электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
Курсовая работа
Исследование искажений сигналов на выходе фильтра нижних частот
вариант № 9
Выполнил: Михайлов Д.А.
Группа: 2583
Факультет: ИБС
Проверил: Барков А.П.
Санкт-Петербург
2014
Содержание
-
Техническое задание.......................................................................................................
-
Нормирование параметров.............................................................................................
-
Определение передаточной функции цепи H(s)...........................................................
-
Расчет частотных характеристик цепи H(jω)...................................................................
-
Составление уравнений состояния цепи.......................................................................
-
Определение переходной h1(t) и импульсной h(t) характеристик..............................
-
Вычисление реакции цепи при воздействии одиночного импульса на входе..........
-
Определение спектральных характеристик одиночного импульса воздействия.....
-
Вычисление спектра реакции при одиночном импульсе на входе............................
-
Определение спектра периодического входного сигнала..........................................
-
Приближенный расчет реакции при периодическом воздействии...........................
-
Заключение.....................................................................................................................
Техническое задание
Цель курсовой работы:
Практическое освоение и сравнение различных методов расчета цепей
Задание к курсовой работе:
На
вход электрической цепи (рис.1) с момента
 подаётся импульс напряжения
подаётся импульс напряжения
 .
Реакцией цепи является
.
Реакцией цепи является
 .График импульса представлен на рис.
.График импульса представлен на рис.

R1 = R2 = 0.36 кОм, L1 = 0.45 мГн, L2 = 0.8 мГн, С = 6180 пкФ
Рис.1

A = 100,
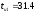 мкс,
мкс,
 , T = tи
, T = tи
1. Нормирование параметров и переменных цепи.
Проведем
нормирование параметров и переменных
цепи выбрав в качестве базисных параметров
 ,
,
 ,
,
 , и получим следующие значения нормированных
параметров:
, и получим следующие значения нормированных
параметров:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Для
простоты записи знак нормировки
 в дальнейшем опускаем.
в дальнейшем опускаем.
2. Определение передаточной функции цепи.
Функция
передачи цепи по напряжению
 , где s- переменная Лапласа.
, где s- переменная Лапласа.
Используем
операторную схему замещения цепи при
нулевых начальных условиях, причем
операторные сопротивления :
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Для
нахождения
 применим метод пропорциональных величин.
применим метод пропорциональных величин.
Составим уравнения по законам Кирхгоффа, и воспользуемся средством автоматизации математических расчетов и вычислений MathCad.
Given

Найдем токи:

Получим:
 ;
;
Для дальнейших расчетов подставим
значения : ,
,
 ,
,
 ,
,
 ,
,
 и примем
и примем
 .
.
Пусть

Тогда:
 ;
;
 ;
;
 ;
;
Таким
образом функция передачи
 ;
;
 ;
;
Произведем
проверку функции
 при
при
 и
и
 ;
;
Составим схемы замещения:
при




 ;
;
 ;
;
Функция
 найдена
верно.
найдена
верно.
при




 ;
;
 ;
;
Найдем полюсы
 (корни характеристического полинома
цепи )
(корни характеристического полинома
цепи )

 ;
;



Расположение полюсов и нулей передаточной функции на комплексной плоскости.

Оценим практическую длительность переходных процессов.
 ;
;
 ;
;
3. Расчет частотных характеристик цепи.
Обобщенная частотная характеристика.
Обобщенной
частотной характеристикой цепи
 называется отношение комплексной
амплитуды реакции к единственному в
цепи воздействию.
называется отношение комплексной
амплитуды реакции к единственному в
цепи воздействию.
 ;
;
 ;
;
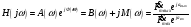 ;
;
 ;
;

 rectangular
rectangular
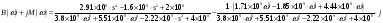
Амплитудно-частотная характеристика(АЧХ):
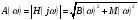 ;
;

Фазо-частотная характеристика (ФЧХ):
 ;
;


Амплитудно-фазовая характеристика.
На графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики такой график объединяет на одной плоскости амплитудно-частотную и фазо-частотную характеристики.
Определим
полосу пропускания на уровне
 ;
;
Определим частоту среза.
 ;
;
Find =0.42;
=0.42;
 ;
;
Полоса пропускания составляет частоты от 0 до 42.
Оценим время запаздывания по наклону графика ФЧХ в области нижних частот.
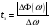 , где
, где
 -приращение
фазы, измеренное в радианах;
-приращение
фазы, измеренное в радианах;
 -приращение
частоты в области нижних частот. Для
ФНЧ также можно использовать формулу
-приращение
частоты в области нижних частот. Для
ФНЧ также можно использовать формулу
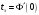 ;
;
 ;
;

Время
запаздывания
 .
.
4. Составление уравнения состояния цепи.
Составим
уравнения по законам Кирхгофа по схеме
замещения для
 используя метод вспомогательных
источников. В исходной схеме после
коммутации заменяем С-элемент источником
напряжения с напряжением
используя метод вспомогательных
источников. В исходной схеме после
коммутации заменяем С-элемент источником
напряжения с напряжением
 , а L-элемент источником
тока с током
, а L-элемент источником
тока с током
 .
.







В матричной форме:
 ;
;
Находим частоты собственных колебаний цепи. Для этого записываем характеристическое уравнение (характеристический полином цепи).







Корни характеристического полинома – частоты собственных колебаний цепи.
Так как корни характеристического полинома равны полюсам передаточной
функции – уравнения состояния цепи составлены правильно.
5. Определение переходной и импульсной характеристик.
Для аналитического расчета переходной характеристики используем операторный метод:


Таким образом переходная характеристика имеет вид:

Также выполним численный расчет переходной характеристики, для этого найдем численное решение уравнений состояния на основе алгоритма Эйлера:
 ;
;

 ,
, ,
,

 ,
,

Начальные значения тока и напряжения.
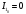 ,
,
 ,
,
 .
.
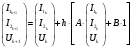

Шаг
расчета выбираем, исходя из условия
 , где
, где
 -
минимальный период колебаний синусоидальной
составляющей в описании процессов в
цепи,
-
минимальный период колебаний синусоидальной
составляющей в описании процессов в
цепи,
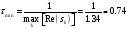 - минимальная постоянная времени,
- минимальная постоянная времени,
 -полюсы передаточной функции цепи.
Выбираем в качестве шага
-полюсы передаточной функции цепи.
Выбираем в качестве шага
 т.к.
т.к.
 .
.
График переходной характеристики при аналитическом и численном расчете.
При увеличении количества точек и
уменьшении шага возрастает точность и
графики сливаются что доказывает
правильность построения. При шаге
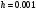 и количестве точек
и количестве точек
 .
.
Найдем импульсную характеристику.


6. Вычисление реакции при воздействии одиночного импульса .
6.1

6.2

