2.4. Модели потоков
Под случайным потоком понимается некоторая последовательность событий. наступающих в случайные моменты времени.
В теории сетей передачи данных применяются понятия потоков сообщений, перерывов связи, ошибок в каналах.
Соответствующие события: поступление сообщений, перерывы связи. ошибки в каналах.
Случайный поток может быть задан функцией распределения величины промежутка времени между моментами наступления событий
=
,P
(
≤ t)
Если
величины
независимы в
совокупности, то поток называется с
ограниченным
последействием.
В
случае P
(
≤t)
= P
(
≤t)
для всех i
≥ 2 поток
является рекуррентным.
Если
P
(
≤t)
= P
(
≤t)
для всех i
≥ 1, то это
поток без
последействия.
Рекуррентный поток называется пуассоновскис, для которого
P
(
≤t)
= 1 –
Для
такого потока вероятность наступления
n
событий за
промежуток времени [0,t]
,
а
математическое ожидание числа событий,
наступивших за время t,
есть
– среднее число событий, поступающих
в единицу времени.
Пуассоновский поток характеризуется отсутствием последействия.
Если, кроме того, соблюдается условие стационарности и ординарности, то пуассоновский поток будет простейшим.
Величина
в случае пуассоновского потока называетсяинтенсивностью
потока событий.
Если
=const?
то поток является регулярным или
детерминированным.
В результате детерминированной операции просеивания образуется поток, который Эрланга, который ближе к егулярному относительно исходного потока (т.е. менее случаен).
2.2. Аналитический анализ смо
2.2.1. Экспоненциальная система массового обслуживания
2.2.1.1 Одноканальная однородная экспоненциальная СМО
Рис. 2.3
Приходы заявок образуют пуассоновский поток событий. Это означает, что время между приходами любых двух последовательных заявок есть независимая случайная величина с экспоненциальной функцией распределения вероятностей
F(Х)
=
(2.6)
Одноканальная
экспоненциальная СМО задается параметрами
λ,
.
Цель ее анализа заключается в расчете
характеристик, важнейшие из которых
следующие:
- коэффициент загрузки ρ;
- средняя длина L очереди;
- среднее число М заявок в СМО;
-
среднее время
ожидания
обслуживания;
-
среднее время
пребывания заявки в СМО.
Коэффициент загрузки рассчитывается по формуле
ρ
= λ ·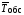
.
(2.7)
Если выполняется условие
ρ ≤ 1, (2.8)
то существует стационарный режим функционирования СМО.
В стационарном режиме среднее число М заявок в СМО постоянно. Следовательно, в стационарном режиме интенсивность потока уходящих заявок равна λ. Коэффициент загрузки ρ в стационарном режиме есть:
а) среднее значение той части единицы времени, в течение которой канал занят;
б) вероятность того, что канал занят;
в) среднее число заявок в канале.
Средняя длина очереди (среднее число заявок в очереди) в одноканальной экспоненциальной СМО рассчитывается по формуле
(2.9)
Среднее число М заявок в СМО равно сумме среднего числа L заявок в очереди и среднего числа ρ заявок в канале:
М=
(2.10)
Заявка перемещается в очереди в среднем с постоянной скоростью. Среднее число переходов заявки в очереди на одно место вперед за единицу времени равно λ.
При такой скорости перемещения L переходов произойдет за время, равное в среднем
=
(2.11)
Формула (2.11) дает среднее время прохождения заявки через очередь. Это есть среднее время ожидания.
Среднее время пребывания заявки в СМО есть
=
(2.12)
Вероятность наличия в системе k требований определяется с помощью геометрического закона распределения в виде
Многоканальная экспоненциальная СМО отличается от одноканальной следующим. Число каналов в ней более одного. Приходящая заявка становится в очередь, если все каналы заняты. В противном случае заявка занимает свободный канал.