2. Математические схемы моделирования систем

2.1. Основные подходы к построению мм систем

Математическую схему можно определить как звено при переходе от содержательного к формализованному описанию процесса функционирования системы с учётом воздействия внешней среды.

«Выстраивается» как бы цепочка: содержательно описание кон

аналитическая модель

цептуальная модель математическая схема

имитационная модель

(концепция – лат.conceptio – восприятие) способ рассмотрения каких-либо явлений, понимание чего-либо; общий замысел чего-либо).

ММ системы S, можно представить в виде совокупностей величин, описывающих процесс функционирования реальной системы:

- входных воздействий х_iХ, i=1…n_x;

- воздействий внешней среды v_lV, l=1…n_v;

- внутренних (собственных) параметров h_kH, k=1…n_h;

- выходных характеристик системы y_jY, j=1…n_y.

–независимые (экзогенные) переменные (детерминированные,стохастические), -зависимые переменные (эндогенные).

Процесс функционирования S описывается оператором F_S:

(2.1)

(2.1) - динамическая модель системы S. Статическая ММ

(2.2)

Соотношения (2.1), (2.2) могут быть получены через свойства системы в конкретные моменты времени, называемые состояниями.

Состояние системы S в интервале времени t₀ < t  T^l полностью определяется c помощью 2-х векторных уравнений:

; (2.3)

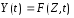. (2.4)

иначе: . (2.5)

Совокупность всех возможных значений состояний {} называется пространством состояний объекта моделированияZ, причём z_kZ.

Время в мод. S может рассматриваться на интервале моделирования (t₀, T) как непререрывное., так и дискретное, квантованное на отрезке длин. t.

Таким образом под ММ объекта понимаем конечное множество переменных {} вместе с математическими связями между ними и характеристиками.

Моделирование называется детерминированным, если операторы F, Ф детерминированные, т.е. для конкретного входа выход детерминированный.

Моделирование называется стохастическим, если операторы F, Ф случайны, т.е. для конкретного входа выход характеризуется определенным распределением вероятностей возможных своих значений.

Детерминированное моделирование - частный случай стохастического моделирования.

В практике моделирование используют типовые математические схемы: диф. уравнения, конечные и вероятностные автоматы, СМО и т.д.

Типовые математические схемы имеют преимущество простоты и наглядности, но при существенном сужении возможности применения.

В качестве детерминированных моделей для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные и др. уравнения, а для представления систем, функционирующих в дискретном времени — конечные автоматы и конечно разностные схемы.

В качестве стохастических моделей для представления систем с дискретным временем используются вероятностные автоматы, а для представления систем с непрерывным временем — системы массового обслуживания (СМО).

Большое практическое значение при исследовании сложных индивидуальных управленческих систем имеют так называемые агрегативные модели. При агрегативном описании сложный объект расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей.