Вопросы и задания

1. От каких величин зависит требуемое число опытов? Откуда берутся их численные значения?

2. Во сколько раз надо увеличить число опытов, чтобы снизить погрешность в 10 раз?

3. Приведите алгоритм моделирования отдельных случайных событий.

4. Приведите алгоритм генерирование зависимых случайных событий.

5. Какие методы тестирования датчиков БСВ Вы знаете? Приведите примеры.

6. Как можно оценить коэффициент корреляции с.в.? Что он показывает?

7. Перечислите характеристики, которыми задается генератор заявок.

8. Раскройте суть метода Монте-Карло.

9. Каким образом реализуется приоритетное обслуживание заявок?

10. Объясните, каким образом решается задача планирования статистического эксперимента.

11. Какими методами может быть оценена точность результатов моделирования?

12. Объясните каким образом осуществляется моделирование сложных случайных событий.

13. Объясните схему статистического эксперимента с автоостановом, изображенную на рис. 9.3.

10. Планирование машинных экспериментов с моделями систем

1. Методы планирования эксперимента на модели.

Основная задача планирования– получение необходимой информации при минимальных или ограниченных затратах машинных ресурсов (машинного времени, памяти и т.п.) на реализацию процесса моделирования.

Отличие от натурных экспериментов:

1) простота повторных условий эксперимента на ЭВМ с моделью 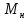системыS;

2) возможность управления экспериментом с моделью (прерывание, возобновление);

3) легкость варьирования условий проведения экспериментов (воздействий внешней среды, параметров и структуры модели);

4) трудности, связанные с определением интервала моделирования, наличие корреляции между последовательностью случайных чисел в процессе моделирования.

Модель

Рис. 10.1. Схема эксперимента

В планировании эксперимента (ПЭ) различают входные (изогенные) и выходные (эндогенные) переменные: х₁, х₂,…, х_к; y_1, y₂…, y_e (рис.1). Входные переменные в теории ПЭ называют факторами а выходные — реакциями.

Каждый фактор x_i, i=1,2,…,k может принимать в эксперименте одно или несколько значений, называемых уровнями.

Каждому фиксированному набору уровней факторов точка в факторном пространстве.

Реакцию (отклик) системы можно представить в виде зависимости

y_l =_l(x₁, x₂,…,x_k); l=1…m. Функцию _l, связанную с факторами, называют функцией отклика, а её геометрический образ – поверхностью отклика. Исследователю заранее не известен вид зависимостей _l, l=1…m, поэтому используют приближение соотношения:

Зависимости _l находятся по результатам эксперимента (по существу – это цель эксперимента).

Факторы при проведении эксперимента могут быть:

– управляемыми и неуправляемыми,

– количественными или качественными,

– фиксированными и случайными,

– изучаемыми и неизучаемыми,

– фиксированными и случайными

Фактор относится к изучаемым, если он включён в модель для изучения свойств системы. Количественными факторами являются интенсивности входящих потоков заявок, интенсивности потоков обслуживания, ёмкости накопителей, количество обслуживающих каналов и другие. Качественным факторам не соответствует числовая шкала (дисциплины постановки на очередь, обслуживания).

Фактор является управляемым, если его уровни целенаправленно выбираются экспериментатором.

При планировании эксперимента обычно изменяются несколько факторов.

Основными требованиями, предъявляемыми к факторам - независимость и совместимость. Совместимость означает, что все комбинации факторов осуществимы.

Для выявления влияния факторов на искомые характеристики необходимо:

– отобрать факторы ,i = , влияющие на искомую характеристику, и описать функциональную зависимость (делаем, когда строим модель);

– установить диапазон изменения значений факторов ;

– определить координаты точек фазового пространства в которых следует проводть эксперимент;

– оценить необходимое число реализаций и их порядок в эксперименте.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.

Практика показывает, что для получения достаточно точных оценок можно обойтись малым количеством опытов, вводя понятие дробного факторного эксперимента (или дробных реплик), который представляет собой некоторую часть (1/2, 1/4, 1/8, и т. д.) от полного факторного эксперимента.

Различают стратегическое и тактическое планирование машинных экспериментов с моделями систем.

Стратегическое планирование ставит своей целью получение необходимой информации о системе S с помощью модели M_M, реализованной на ЭВМ.

Тактическое планирование – определяет способы проведения каждой серии испытаний машинной модели M_M.

Стратегическое планирование лежит в основе разработки плана. Основные проблемы, которые приходится решать: большое количество факторов (сокращение факторного пространства); многокомпонентность функции реакции; стохастическая сходимость результатов машинного эксперимента; ограниченность машинных ресурсов.

Проблема стохастической сходимости результатов машинного эксперимента. Выходные характеристики – выборочные средние, найденные путём многократны прогонов модели на ЭВМ. Сходимость выборочных средних к средним значениям с ростом объема выборки называется стохастической. Эта сходимость, как правило, медленная. Если  - стандартное отклонение одного наблюдения, то стандартное отклонение среднего N наблюдений будет равно , т.е. для уменьшения ошибки случайной выборки вk раз требуется увеличить объем выборки в k² раз.

Медленная сходимость преодолевается применением ускоренных методов моделирования, обеспечивающих снижение дисперсии оценки (расслоенная выборка, взвешенная выборка и др.).

Выделяют этапы стратегического планирования:

1) построение структурной модели;

2) построение функциональной модели.

Структурная модель выбирается исходя из того, что должно быть сделано, характеризуется числом факторов и числом уровней для каждого фактора.

Число элементов эксперимента N_с= q₁,q₂…q_k, где k – число факторов, ,– число уровнейi – фактора.

Элемент структурной модели – структурный блок эксперимента, определяемый как простейший эксперимент в случае одного фактора и одного уровня.

Необходимо выделять наиболее существенные факторы. Выделять уровни. Минимальное число уровней каждого фактора равно 2.

Анализ результатов существенно упрощается, если уровни равноотстоят друг от друга.

Аналитические упрощения. если ,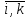– симметричная структурная модель, т.е.=,.

Функциональная модель ПЭ определяет количество элементов структурной модели, т.е. необходимое число различных информационных точек N_ф.

Функциональная модель может быть полной (N_ф=N_с) и неполной (N_ф<N_с).

Основная цель построения функциональной модели – нахождение компромисса между необходимыми действиями и ограничением ресурсов.

Для анализа возможностей рассматривают попарно относительное влияние числа факторов. числа уровней и числа повторений на количество необходимых машинных прогонов N модели.

Пусть полное число прогонов при симметрично повторяемом эксперименте равно n – необходимое число повторений эксперимента, q– число уровней каждого фактора, k– число факторов.

Какая из трех величин дает наибольшее сокращение полного количества прогонов?

= ;=;=.

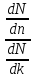Анализ приведенных отношений показывает:

1) если kn > q и k > qlnq, то доминирует q;

2) если k < qlnq и nlnq > 1, то доминирует k ;

3) если nlnq < 1 и q > kn, то доминирует n.

(доминирует – обеспечивает более крутую производную).

Таким образом. использование структурных и функциональных моделей позволяет рационально построить план эксперимента с учетом наличных ресурсов.

Тактическое планирование машинных экспериментов

Здесь решают проблемы:

• определения начальных условий и их влияния на достижения установившегося результата при моделировании; определяется влиянием переходного периода;

• обеспечения точности и достоверности результатов моделирования; реализуется через дисперсию оценки;

• уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем; реализуется через применение методов понижения дисперсии

• выбора правил автоматической остановки имитационного эксперимента с моделями; применение метода автоостонова.