
- •1. Наличие цели
- •1.3. Классификация моделей
- •1.4. Методы моделирования
- •2. Математические схемы моделирования систем
- •2.1. Основные подходы к построению мм систем
- •2.2. Задачи, решаемые с помощью моделирования
- •2.3. Система массового обслуживания как модель
- •2.4. Модели потоков
- •2.2. Аналитический анализ смо
- •2.2.1. Экспоненциальная система массового обслуживания
- •2.2.1.2. Многоканальная экспоненциальная смо
- •2.2.1.3. Модель m/g /1
- •2.3. Сети массового обслуживания
- •2.4. Анализ разомкнутых экспоненциальных СеМо
- •2.4.1. Свойства разомкнутой экспоненциальной СеМо
- •2.5. Расчет системных характеристик экспоненциальных СеМо
- •Контрольные вопросы
- •Пример 1. Проблема распределение канала
- •1. Статическое распределение канала
- •2. Динамическое распределение канала
- •Пример: расчет системы телеобработки данных
- •3.1. Задание
- •3.2. Решение
- •4. Схема расчета замкнутой СеМо
- •4. Имитационное моделирование систем массового обслуживания
- •4.1. Система массового обслуживания как модель и оригинал
- •4.2. Иллюстративный пример: моделирование посадки самолетов.
- •4.3. Пример: оценка надежности системы
- •Рассмотрим случайную величину
- •5. Построение моделирующего алгоритма
- •5.1. Моделирование на эвм процесса функционирования смо
- •Шагом (принцип t)
- •С другой стороны, принцип особых моментов выгоден тем, что
- •5.2. Особенности реализации процессов с использованием q-схем
- •5.2. Примеры моделирования смо с отказами
- •5.2.1. Подготовка исходных данных и назначение переменных
- •Моделирование смо с отказами по схеме событий
- •5.2.2.1. Построение блок-схем алгоритма имитации
- •Моделирование смо с отказами по схеме событий
- •5.3. Схемы построения моделирующего алгоритма
- •5.4. Моделирование смо с отказами по схеме процессов
- •Моделирование смо с отказами по схеме процессов
- •Шаг имитации
- •Класс процессов "генерирование заявок источником"
- •Численный пример
- •5.5. Семафоры и связные списки
- •5.6. Алгоритмы обслуживания очередей
- •1) Традиционный алгоритм fifo
- •2) Приоритетное обслуживание (Priority Queuing)
- •3) Взвешенные настраиваемые очереди (Weighted Queuing)
- •6. Оценки искомых характеристик и их дисперсии
- •6.1. Структура оценок
- •7. Моделирование случайных факторов
- •8. Тестирование имитационной модели
- •9. Планирование статистического эксперимента
- •Вопросы и задания
- •Планирование машинных экспериментов с моделями систем
- •Методы планирования эксперимента на модели.
- •11. Замечание о языках моделирования
- •Моделирование смо с одним npи6opом и очередью
4.2. Иллюстративный пример: моделирование посадки самолетов.
Цель: определение необходимого количества посадочных полос.
Самолеты пребывают в зону и подают заявку на посадку в случайные моменты времени (рис. 4.1).

 –интервал
между соседними заявками;
–интервал
между соседними заявками;
 –интервал
обслуживания отдельной заявки.
–интервал
обслуживания отдельной заявки.
Рис. 4.1. Имитация процесса посадки самолетов
 –интервал
между соседними заявками задается
–интервал
между соседними заявками задается
 .
.
Если
в момент подачи заявки полоса свободна
– начинается процесс посадки, который
длится фиксированное время
 .В течение этого
времени полоса занята.
.В течение этого
времени полоса занята.
Если в момент поступления очередной заявки полоса занята – такая заявка получает отказ. Это нежелательное событие. Если часто отказ – необходима дополнительная полоса. Непосредственная цль моделирования – нахождение (оценивание) вероятности отказа Р.
Процесс смены состояний – дискретный. Время – непрерывное. Особые моменты – моменты поступления заявок и моменты освобождения полосы.
Имитация процесса на ЭВМ: воспроизведение шаг за шагом численных значений особых моментов и значений переменных в эти моменты.
В памяти ЭВМ достаточно отвести одну или несколько ячеек для каждой из характеристик имитируемого процесса и обновлять содержимое этих ячеек, имитируя изменение характеристик во времени.
Перечислим переменные, которые должны хранится и обновляться в памяти ЭВМ для данного примера:
tт – текущий особый момент;
tз – предстоящий момент поступления очередной заявки (ближайший из таких моменов после tт);
tосв – предстоящий момент освобождения полосы;
Z – состояние полося в особый момент (непосредственно перед tт);
n – количество заявок, поступивших к текущему моменту;
к – количество отказов, наблюдавшихся за то же время.
Счетчики
n
и к накапливают
статистики
(выборочные
данные), по которым определяется оценка
 =
= .
.
Правило
остановки
процесса имитации: когда значение n
достигнет
значения
 (надо задать).
(надо задать).
Исходные
данные:
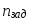 ,
,
 (F(x)
– специальная
подпрограмма). Помимо указанных переменных
используются:
(F(x)
– специальная
подпрограмма). Помимо указанных переменных
используются:
-–
 ,
, ,параметры F(x)
– постоянные;
,параметры F(x)
– постоянные;
–– Вспомогательные
переменные:
 ,Е – (event
– событие) содержит тип события: 1 –
поступление заявки, 0 – освобождение
полосы; Z
L(Last
– прошлое) – представляет предыдущее
значение Z.
,Е – (event
– событие) содержит тип события: 1 –
поступление заявки, 0 – освобождение
полосы; Z
L(Last
– прошлое) – представляет предыдущее
значение Z.
Как следует из приведенного примера, имитация, как процесс, заключается в организации продвижения системного времени и отображения в нем траектории функционирования оригинала. В данном примере – отображении процессов генерации заявок и их обслуживании. Функционирование отображается сменой состояний оригинала. Ибо смена состояний дает информацию, по которой можно вычислить интересующие исследователя (проектировщика) оценки характеристик оригинала.
Если система (оригинал) стохастическая, то пребывание системы в том или ином состоянии (вектор) и наступление состояний носят вероятностный характер.
Таким образом, имитационное моделирование включает два важнейших аспекта: построение моделирующего алгоритма и разыгрывание состояний системы. Моделирующий алгоритм обеспечивает продвижение системного времени и отображение состояний системы, а реализация случайных факторов и объектов, присущих системе, осуществляется методом статистических испытаний – методом Монте-Карло.
4.3. Концепция статистического моделирования
В основе статистического моделирования лежит процедура, применяемая для моделирования случайных величин и функций и носящая название метода статистических испытаний (метод Монте-Карло).
Общая схема метода Монте-Карло может быть записана в виде
 (4.1)
(4.1)
Результат ищется как математическое ожидание некоторой случайной величины Y, которая чаще всего является неслучайной функцией случайной величины X, имеющей распределение р(х). Случайная величина Х имеет распределение р(х) и запись Х р(х) означает, для непрерывной случайной величины, что для непрерывной случайной величины плотность вероятности равна р(х); для дискретной случайной величины функцию р(х) надо понимать как функцию вероятности. Для случайной дискретной величины интеграл (4.1) заменяется суммойу(х) р(х), в которой суммирование осуществляется по всем возможным значениям Х. Функция у(х) может иметь несколько аргументов, т.е. зависеть от нескольких случайных величин. В таком случае запись (4.1) остается в силе, только интеграл надо считать многомерным, Х рассматривать как вектор, а р(х) – как многомерную плотность (или функцию) вероятности. Приближенная оценка неизвестного математического ожидания, совпадающая с искомым результатом, находится как среднее арифметическое результатов независимых опытов. Это отражено в правой части (4.1). По закону больших чисел среднее арифметическое сходится к математическому ожиданию.
В каждом опыте разыгрывается реализация
х случайной величины Х (в i- м опыте
реализация
 )
в соответствии с распределением р(х) и
вычисляется значение функции в виде у
(
)
в соответствии с распределением р(х) и
вычисляется значение функции в виде у
(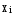 ).
Индекс i подчеркивает, что для каждой
(i-й) реализации процесса аргументы,
составляющие вектор Х, имеют свои
случайные значения. Вычисленное очередное
значение у (
).
Индекс i подчеркивает, что для каждой
(i-й) реализации процесса аргументы,
составляющие вектор Х, имеют свои
случайные значения. Вычисленное очередное
значение у ( )
добавляется к накапливаемой суммеу (
)
добавляется к накапливаемой суммеу ( ).
На этом заканчивается очередной опыт.
После того как проведено М опытов,
вычисляется итоговая оценка в виде
правой части выражения (4.1). Опыты
повторяются до тех пор, пока дисперсия
оценки
).
На этом заканчивается очередной опыт.
После того как проведено М опытов,
вычисляется итоговая оценка в виде
правой части выражения (4.1). Опыты
повторяются до тех пор, пока дисперсия
оценки не снизится до требуемой величины,
зависящей от допустимой погрешности и
коэффициента доверия. Структурная схема
эксперимента по имитационному
моделированию представлена на рис. 4.2.
не снизится до требуемой величины,
зависящей от допустимой погрешности и
коэффициента доверия. Структурная схема
эксперимента по имитационному
моделированию представлена на рис. 4.2.
