Функции / Линии второго порядка / Привести к простейшему виду уравнение кривой 5x2

Привести к простейшему виду уравнение кривой 5x² + 4xy + 8y² - 32x - 56y + 80 = 0.

Решение.

Начнем с поворота осей. Целью этого преобразования является уничтожение в преобразованном уравнении члена, содержащего произведение текущих координат. Формулы преобразования координат поворотом осей без изменения начала координат имеют вид

Подставляя эти значения x и y в заданное уравнение, будем иметь

Раскроем скобки и получим

Сделаем приведение подобных членов:

     (A)

Выберем теперь угол поворота   так, чтобы коэффициент при x₁y₁ обратится в нуль. Приравнивая этот коэффициент нулю, получаем уравнение для определения значения угла  , при котором этот коэффициент обратится в нуль:

Разделим обе части этого уравнения на   ( , так как если  , то  , и тогда это уравнение не имеет места, т. к. получается, что -4 = 0. Это замечание следует помнить и при решении последующих задач). После деления получим

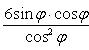
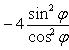
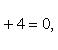
или после упрощений

Отсюда получаем для тангенса угла   поворота координатных осей такие значения:

или

 и  .

Эти два значения   соответствуют двум взаимно перпендикулярным направлениям, так как произведение этих тангенсов равно -1. Из   следует, что угол поворота   может находиться в первой или третьей четвертях, а из   следует, что угол поворота   может находиться во второй или четвертой четвертях. Условимся всегда брать для   из двух возможных значений - положительное, а угол поворота   - в первой четверти  . Таким образом, из двух возможных значений тангенса берем  .

Определим по известному   величину   и  . Это нужно для того, чтобы определить коэффициенты при   и y₁ в уравнении (A).

Так как у нас  , а угол   находится в первой четверти, то по известному   функции   и   могут быть определены следующим образом:

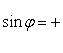
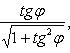
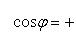
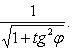
Из этого следует, что  ,

При найденных значениях   и   коэффициент при   равен 9, коэффициент при x₁y₁ - нулю, при   равен 4, коэффициент при x₁ равен  , а при y₁ равен  . Подставляя эти значения в уравнение (A) и поступая так же, как в задаче, получим

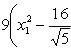
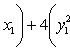
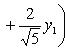
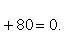
Выделяя в скобках полные квадраты, имеем

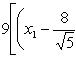
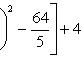
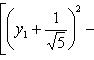
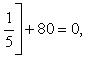
откуда

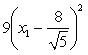
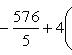
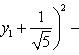
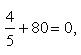
или

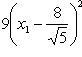
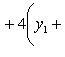
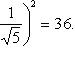     (B)

Сделаем теперь параллельный перенос координатной системы x₁Oy₁ (см. рисунок).

Формулы преобразования запишем так:

     (1)

и

     (2)

Теперь в уравнение (B) введем обозначения  ; из сравнения с формулами (2) заключаем, что  , а уравнение (B) перепишем так:

После деления обеих частей равенства на 36 получим данное уравнение в каноническом виде:

Итак, данное уравнение определяет эллипс. Он вытянут вдоль оси O₁y₂. Эскиз кривой показан на рисунке.

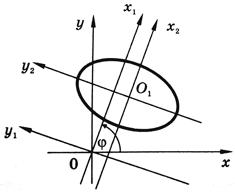
Докажите, что точка O₁ - центр эллипса - в исходной системе координат имеет координаты (2, 3).

Принимая во внимание, что  , а x₁ = x₂ + x₀; y₁ = y₂ + y₀, получаем, что